新型立式行星减速机自润滑装置分析与优化

苏昌盛，闫永生，王润军，夏 岩，叶金铎，张春秋*

（1.天津理工大学a.天津市先进机电系统设计与智能控制重点实验室，b.机电工程国家级实验教学示范中心，天津 300384；2.沈阳露天采矿设备制造有限公司，辽宁 沈阳 110041）

立式行星减速机应用广泛，例如建筑机械、冶金起重机械、矿用挖掘机等的行走机构都使用了立式行星减速机作为传动装置。为了保障行星减速机能流畅运行以及能够有较长的使用寿命，通常需要在行星减速机内部注入一定量的润滑油，使行星减速机内的各个传动机构能够得到良好的润滑。传统润滑方式一般有2种，一种是齿轮旋转搅动油池内润滑油飞溅至齿轮箱内各部分实现润滑，此种方式需要在机壳内壁加工相应的回油槽，加工工艺复杂[1]。该方式只适用于传动比较小的立式行星减速机，且会出现高速轴齿润滑、冷却不良导致齿面胶合、轴承失效等现象[2]。另一种是外加润滑泵喷油润滑的方式，对液面以上的轴承进行润滑和降温。但是其外部附加系统较多，易发生故障，特别是工作环境恶劣时喷油泵易发生损坏，相关零件得不到同步润滑，行星减速机零件容易损坏，可靠性较差[3]。

本文提出一种新型立式行星减速机自润滑方式，该润滑装置体积小，重量轻，承载能力大，传动效率高，结构紧凑，喷油润滑技术结构上更容易实现且具有良好的润滑效果[4]。在三维软件中建立三维油管模型，利用有限元软件，采用气液两相流方法对不同转速和不同入射角工况下自润滑装置油管的喷射性能进行仿真分析，并在此基础上对油管进口提出优化方案，提升喷射性能。

1 自润滑装置的建模

此次研究的立式行星减速机自润滑机构包括开油槽的弧形钢板和油管，通过螺钉固定在立式行星减速机的内齿联轴器上。油管直径和油管与水平线的夹角由油管角度与流量的设计曲线确定，油管直径为4.8 mm。为了保证立式减速机在正转和反转时都能够进行自润滑和降温，上部轴承润滑和降温的油管设置2个，一个按照右旋设计，一个按照左旋设计。导油管的底部位于润滑油的液面下10～50 mm，油管的切口采用径向截面切割，保证立式行星减速器在旋转时，油管切面的法线沿内齿联轴器的圆周的切线方向。立式联轴器的上部轴承挡圈开有一定数量的回油孔，能够让导油管在完成上部轴承润滑和降温之后回流到立式减速机的储油舱内，回油孔的数量和直径按照自润滑油的流量确定。图1为自润滑装置图，图2为减速机上部结构图。

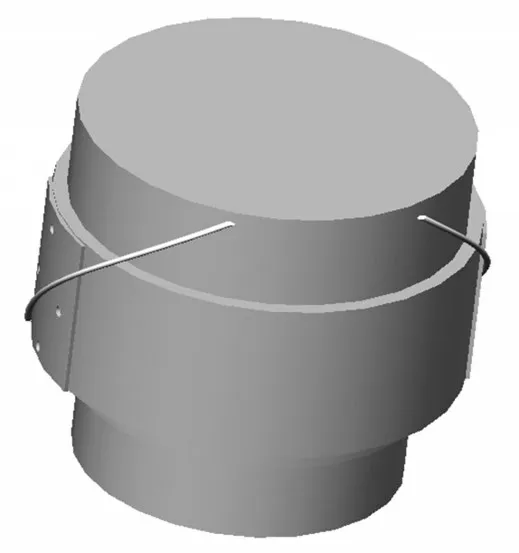
图1 自润滑装置图Fig.1 Self-lubricating device diagram

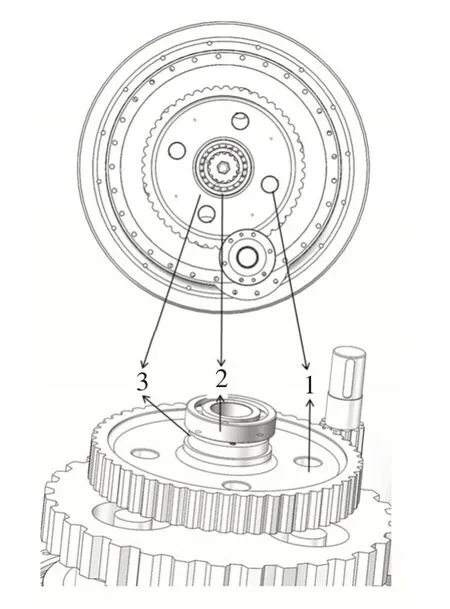
图2 减速机上部结构图Fig.2 Upper structure diagram of reducer

有限元模型必须与分析目的和计算机性能匹配，并不是模型越精确计算精度就越高。要求越精确就意味着模型越复杂，进而要求软件进行更加复杂的矩阵化简求解。这样一来，虽然模型的误差小了，但是计算误差反而增大，导致最终得不到合适的结果。在建立有限元模型时，尽量采用尽可能简单的模型，无需保留对计算结果无影响的部分以及所有的细节特征[5]。因此对本模型进行简化，分析得出内齿联轴和弧形钢板对计算结果并无影响，同时考虑到两个油管的仿真效果是相同的，因此只需要对其中一个进行仿真，图3所示为简化模型。

图3 简化模型Fig.3 Simplified model

2 流体分析与结果

2.1 两相流模型及湍流的选取

本文研究的是油管中的油向空中喷射高度的问题，属于气-液两相流模型。流体中描述两相流有2种方法：欧拉法和拉格朗日法。欧拉法即为两相流模型，拉格朗日法即为离散型，本模型属于两相流模型故选择欧拉法。

欧拉法中两相流模型包括：流体体积函数模型（the volume of fluid，VOF），混合（mixture）模型和欧拉（Eulerian）模型。

VOF模型适用于分层的或自由表面流动的情形，用于处理没有相互穿插的多相流问题；而混合模型和欧拉模型适用于流动中有相混合、分离或分散相的体积分数超过10%的情形[6]。

本模型是有相互穿插的两相流，所以不能用VOF模型。在仿真过程中，液体相通过油管喷向气体相中，只是分散在相应的流体域而不是广泛地分布，加上对仿真结果精度的严要求，最终选择了欧拉模型进行本研究。欧拉模型多应用于数值模拟中，将每个相看作不同流体，然后分别求解每个相的动量方程和连续方程[7]。自润滑装置内是气液混合旋流场，所以考虑使用具有旋流效果的重整化群（re-normalizationgroup，RNG）k-ε模型进行计算[8]。RNGk-ε模型是在k-ε标准模型的基础上，修正了湍流黏度，考虑了平均流动的旋转及旋流流动的改进型模型，所以该模型对于强旋流动的模拟有较高的精度[9]。

2.2 基本方程

q相的质量守恒方程为：

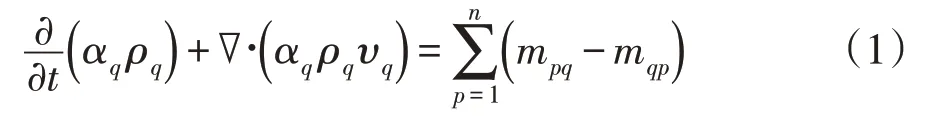
式中，αq，ρq和υq分别表示q相的体积分数、密度和速度，mpq表示p相向q相的质量传递，mqp则相反。

q相的动量守恒方程为：

式中，p为两相共享压力，υpq表示界面速度，Rpq,Fq,Flift,q,Fwl,q,Fvm,q和Ftd,q分别表示相间的相互作用力、外部体积力、升力、壁面润滑力、虚拟质量力和湍动扩散力，τq表示q相的压力应变张量，其计算公式为：

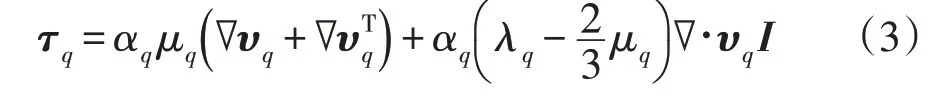
式中，μq和λq分别表示为q相的剪切力黏度和体积黏度，I为单位张量[10]。

2.3 网格划分

将实体模型导入FLUENT mesh软件中，为了加快收敛，需在喷射口处添加喷射流域使其流动变好，该流域根据减速器外直径而确定，图4所示为添加流域图。整体模型相对来说比较简易，为了控制好网格采用了总体网格控制中曲率控制函数和局部网格控制中四面体网格进行划分，整体模型网格数量为2 406 452。

图4 添加流域图Fig.4 Adding a watershed map

2.4 边界条件及求解方法

油管进口不需要设置进口速度，油液在油管旋转的过程中，会在离心力作用下从油管出口喷出。因为不知道油管出口处具体的压力和温度值，所以设置成自由出流。对单元格区域条件使用旋转坐标系，壁面设置成旋转壁面，施加以不同的转速。欧拉模型中空气为主相，润滑油为次相，表1所示为计算参数。

表1 计算参数Tab.1 Calculation parameters

在流体有限元分析软件（ANSYS FLUENT）平台下，选择具有旋流效果的RNGk-ε湍流模型，然后运用相耦合简单（phase coupled simple）算法对离散后的代数方程进行求解。当残差值下降到10-3时或各项指标趋于平缓不再发生变化时收敛。

2.5 结果分析

2.5.1 不同转速下的结果与分析

对润滑油在标准转速750 rpm时的喷射效果进行计算，图5为润滑油喷射效果图。

从图5只能观察出喷出油液的效果，对于具体的喷射高度，需要分别根据转速为300、550、750、900 rpm时油管出口处的最大速度，再结合运动公式，才可计算出油液所能达到的最高高度，表2所示为出口最大速度及对应高度。

图5 润滑油喷射效果图Fig.5 Oil injection effect drawing

将表2数据用Matlab软件平台进行数据拟合，得到的转速与高度关系曲线如图6所示。

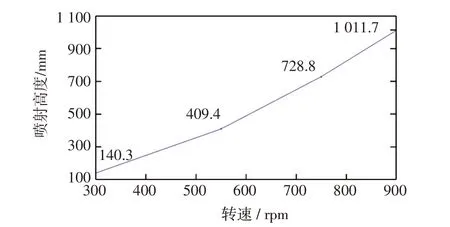
图6 转速与高度关系曲线Fig.6 Speed-height curve

从图6的曲线中可知，转速在300、550、750、900 rpm时的喷射高度分别为140.3、409.4、728.8、1011.7 mm，因此可得随着转速的增加，喷射高度也随之增加，并且趋于线性关系。其原因在于润滑油是黏性流体，求解不仅和边界条件有关，而且也和雷诺数有关。

雷诺数公式为：

式中，υ、ρ、μ分别为流体的流速、密度与动力黏度，d为管道直径。

利用雷诺数可区分流体的流动是层流或湍流。若雷诺数很小，则黏滞力是主要因素，黏滞力对流场的影响大于惯性，分子黏性作用对湍流有着直接影响，流场中流速的扰动会因黏滞力而衰减，流体流动稳定，为层流；若雷诺数很大，则惯性力是主要因素，黏性力项成为次要因素，惯性对流场的影响大于粘滞力，流体流动较不稳定，为湍流。流动状态由层流转变成湍流时的雷诺数称为临界雷诺数。在实践中，雷诺数Re≤2 300为层流，而Re＞2 300为湍流[11]。将数据代进方程得知，转速在300～900 rpm之间其雷诺数均远远大于2 300，所以都属于湍流。再根据纳维叶-斯托克斯（Navier-Stokes）方程[12]计算，该方程为：

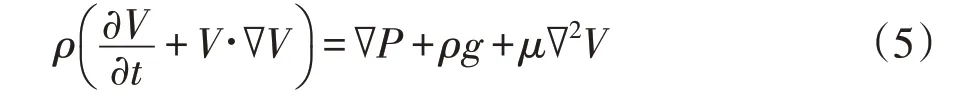
式中，ρ为质量流体密度，为加速度，(∇P+ρg+μ∇2V)为单位体积受到的合力。

公式（5）表示在不同的雷诺数范围内，流体流动不同，物体所受阻力也不同，当雷诺数低时，阻力正比于速度、黏度，而雷诺数高时，阻力大体上正比于速度的平方。

2.5.2 不同入射角度情况下结果与分析

影响油液喷射高度的因素不仅是转速，同时也跟入射角度相关。本节分别考虑了入射角度在30°、45°和60°时不同转速下的喷射高度情况，图7所示为油管不同入射角度图。

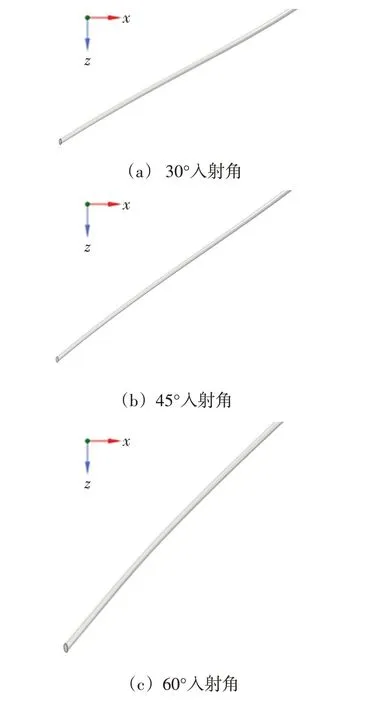
图7 油管不同入射角度图Fig.7 Angle diagram of different incidence of tubing

对以上3个模型分别施加不同转速，得到不同入射角度在不同转速下与喷射高度的关系曲线，图8所示为不同入射角在不同转速下的喷射高度图。

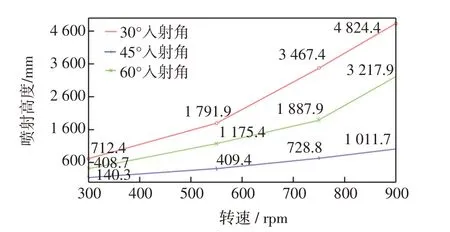
图8 不同入射角在不同转速下的喷射高度图Fig.8 Injection altitude diagram at different incidence angles and different rotational speeds

通过图8可知，在不同入射角情况下，随着转速提高，喷射高度都趋于线性增高趋势。同时也可发现，当入射角度为45°左右时，喷射高度达到最低。在相同转速下，入射角为30°～45°之间时喷射高度随着角度的增加而减小，在45°～60°之间时喷射高度随着角度增加而增大。其原因在于，当入射角度处于45°时，油管的总长度和阻力都相对达到一个较大值。虽然入射角为30°时总长度达到最大，但是所受壁面的阻力达到最小。入射角为60°时阻力达到最大，但是总长度最短。

3 结构优化设计

对自润滑装置模型进行优化，优化流程主要分为5部分：优化设计、三维模型软件（Solidworks）建立优化模型、流体（FLUENT）仿真、结果对比分析和优化方案确定。

3.1 优化设计及建模

造型优化设计主要是通过三维模型软件在原有模型的基础上进行改进，达到在相同转速下喷射高度进一步提高，从而拥有更好的润滑降温作用。设想将油管进口处改进为一个类似于漏斗形式的模型，漏斗外圆直径为9.7 mm，斜度为30°。这样在单位时间内可以使流量加大，促使喷射高度进一步升高，进口优化模型如图9所示。

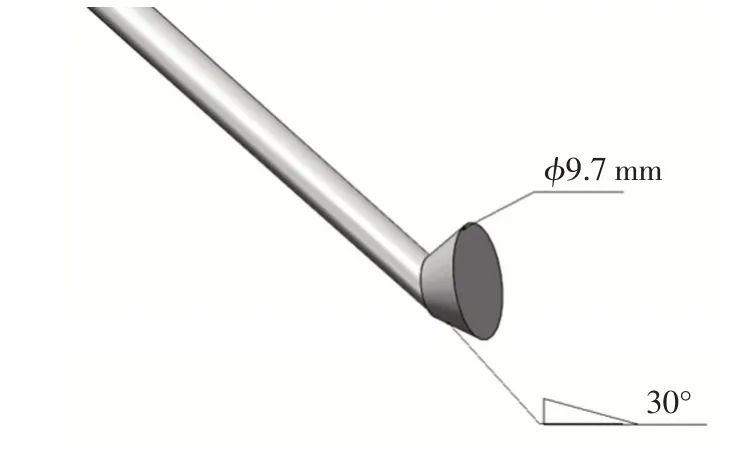
图9 进口优化模型Fig.9 Import optimization model

3.2 仿真结果分析

将优化好的模型进行网格划分、设置相同的两相流模型及边界条件控制等。优化后的模型在标准转速750 rpm条件下进行仿真，将得到的喷射云图和未优化模型750 rpm转速下的喷射云图进行比较，图10所示为模型优化前后对比图。

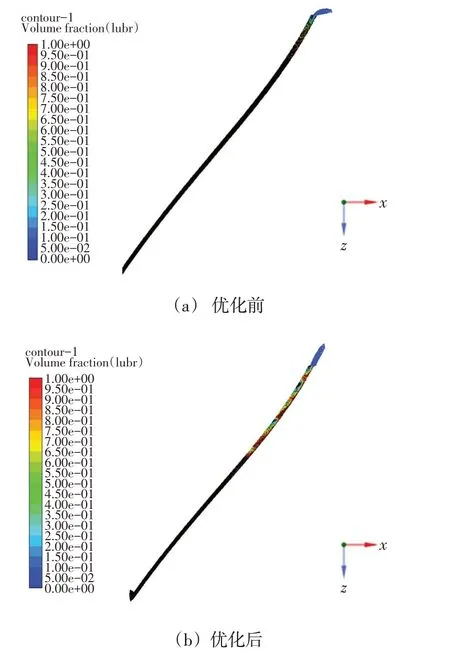
图10 模型优化前后对比图Fig.10 Comparison chart after model optimization

从10图可知，优化后的模型不仅喷射高度更高，同时在柱状宽度方面也好于未优化模型。相比于未优化模型在750 rpm转速时达到的喷射高度728.8 mm，优化后的模型喷射高度达到了2 174.6 mm，效率提升将近200%，优化后的出口最大速度及对应高度如表3所示。

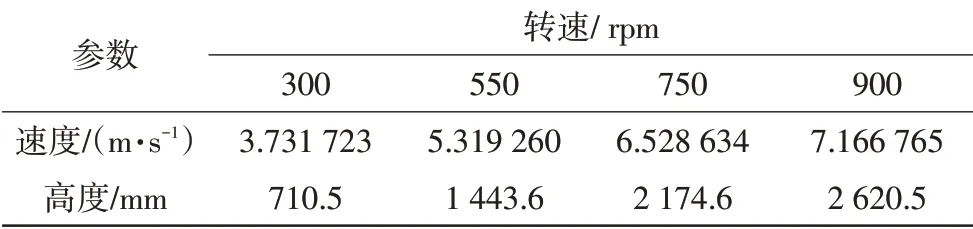
表3 优化后的出口最大速度及对应高度Tab.3 Maximum exit velocity and corresponding height after optimization

用Matlab分别对两组数据进行对比，得到的喷射高度对比图如图11所示，优化后的模型在相同转速下相比于未优化模型喷射高度有大幅度的提高，整体上达到了优化的目的，具有实际应用价值。

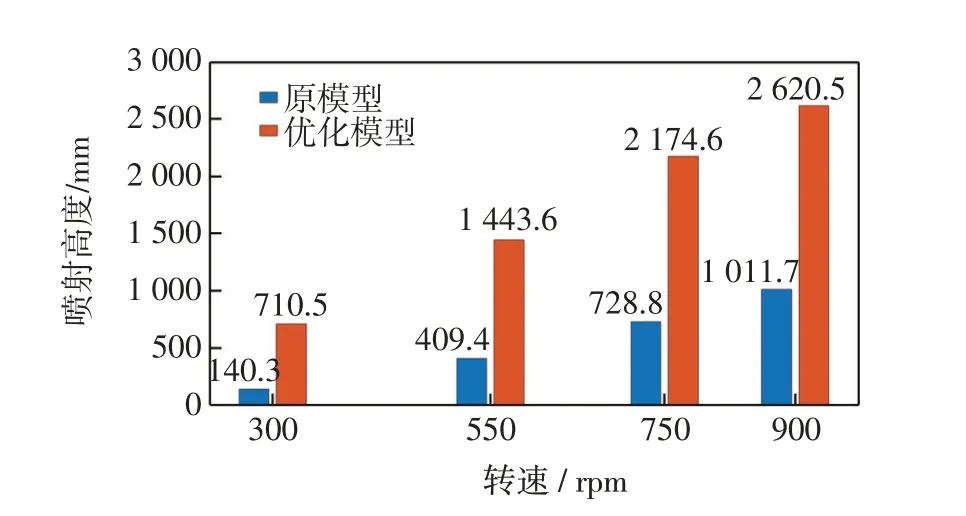
图11 喷射高度对比图Fig.11 Jet height comparison chart

4 结论

1）设计了一种新型立式行星减速机的自润滑装置，替代了原有外加润滑泵喷油润滑的方式，简化了装置，实现了对油面以上轴承的更好的润滑和降温作用。

2）利用欧拉模型实现了自润滑装置内油管向空气中喷油的气液两相流的模拟，并且采取瞬态进行分析，通过出口处的最大速度再结合运动学公式得到具体的喷射高度。

3）喷射高度随着转速的增加而增加，并且趋于线性关系。

4）转速一定时，入射角度在30°～45°之间喷射高度会随着角度的增加而减小，入射角度在45°～60°之间随着角度的增加而增加。

5）对原模型进行了优化，通过与原模型比较，结果提升明显，提高比率皆在100%以上，优化明显，证明了优化后模型的可实施性。