基于有限元模型的煤矿排水管道振动特性分析*
赵鹏程
(1. 中国煤炭科工集团 太原研究院有限公司, 山西 太原 030006;2. 山西天地煤机装备有限公司, 山西 太原 030006)
0 引言
在煤矿开采过程中,随着雨水、附近河流的渗透加上可能发生的采矿区与储水层连通造成的突水现象,大量的积水会聚集在井下,为保障煤矿开采工作的顺利进行,必须及时将积水排出[1-3]。煤矿排水系统由电动机、排水水泵、排水管道和井口支撑附件等组成,较常采用的是离心式水泵,在工作过程中,泵源产生的压力脉动会导致整个管道系统发生强烈的振动,而泵源脉动频率与管道本身的固有频率接近时发生的共振现象会导致振动故障的发生,造成管道破裂、泄漏等问题[4-6]。目前针对排水管道系统的研究主要集中在提高排水效率清洗管道水垢以及排水管道的设计方面,对管道故障方面的研究较少。张世斌等[7]利用有限元分析进行了深井排水系统的疲劳寿命研究,建立了排水管路的三维模型并进行了静载分析和安全性评价。赵福隆等[8]建立了排水管道的有限元模型,基于有限元分析得到了固有频率和振型,验证了管道稳定性。寇彦飞[9]采用水锤防护理论,建立了波动数学模型,研究了矿井排水系统中的管路振动问题。现有的文献对排水管道振动问题的研究方向存在欠缺,因此研究煤矿排水管道系统的振动问题,建立准确的排水管道动力学模型,对煤矿开采工作具有重要的工程应用价值。
1 排水管道系统有限元建模
对于泵源激励下的矿井排水管道系统研究,需要同时考虑管道横向弯曲和摆动振动,因此首先推导管道的振动微分方程,并引入反映单元位移状态的形函数构建振动有限元模型,最后通过单元矩阵组集得出矿井排水管道的整体刚度矩阵。
1.1 振动微分方程的构建
本文采用Timoshenko梁单元对管道系统进行有限元离散,其中第k个梁单元示意图如图1所示,梁单元有2个节点(i和j),每个节点包含2个自由度,其中wi、θyi、wj和θyj分别表示oxyz局部坐标系下两节点的横向位移和转角位移,则单元节点位移向量qe可以定义为:
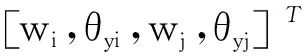
(1)

图1 第k个梁单元
第k个Timoshenko梁单元的势能U和动能T分别为:

(2)
(3)
式中:ρ、l和A分别为单元的密度、长度和截面面积。Iy代表关于oy的截面惯性矩;E和G分别代表杨氏模量和剪切模量,κz代表关于z轴的剪切系数


(4)

(5)
1.2 引入单元形函数
为了求解偏微分方程,引入形函数[11],具体如下:
假设横向位移w和转角位移θy(x)均采用3次多项式进行插值,则有
(6)
(7)
根据位移边界条件结合插值多项式[12],最终可得:
(8)
且Nw1(x)、Nw2(x)、Nw3(x)、Nw4(x)、Nθy1(x)、Nθy2(x)、Nθy3(x)和Nθy4(x)的表达式如下:
(9)
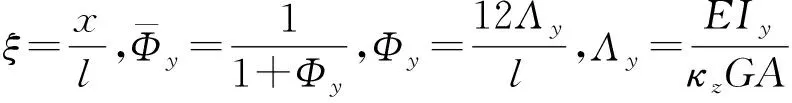
1.3 梁单元的刚度和质量矩阵
将形函数代入到偏微分运动方程中得到单元质量及刚度矩阵为:
(10)

(11)
利用有限元法对单元矩阵进行组集,最终获得排水管道的质量矩阵及刚度矩阵,其动力学方程可以表示为:
(12)
式中:M、C和K分别代表整体质量矩阵、阻尼矩阵和刚度矩阵,Fu是外激励向量。
2 管道的固有特性分析
2.1 管道模态试验
针对煤矿排水系统,选取一段管道进行研究,试验台管道系统的材料是Q345,如图2所示,管道外径为32.8 mm,内径为30 mm,具体参数如表1所示。为获取管道固有频率进行模态锤击试验,用加速度传感器采集信号。采用多点激励、单点拾振的方式来进行试验测试,关于信号采集系统的设置具体如下:设置激励方向和响应方向,建立每个信号通道与试验测点的对应关系,其中力锤信号为触发信号,为了消除噪声影响,每组采用两次平均,得到加速度频响函数如图3所示。

表1 管道材料及几何参数

(a) 实验管道

(b) 仿真管道

图3 管道系统试验频响函数
2.2 管道模态分析
基于有限元理论,根据哈密顿理论和能量原理得到的质量和刚度矩阵进行仿真计算,建立了管道模型,由于实际应用中的排水管道系统一段与泵连接,所以将该段管的边界调节设置为一段固支一段自由,计算得到前5阶固有频率和模态振型,图4为振型对比图,与实验得到的固有频率对比如表2所示。

fn1试验仿真fn2试验仿真fn4试验仿真fn5试验仿真

图4 振型图对比
由表中数据对比发现,仿真数据与实验数据的固有频率误差较小,而且振型图吻合较好,说明所建模型能够较为准确地反应真实管道的振动状态,可以进一步为管道振动的研究提供指导性作用;而且发现煤矿排水管道的固有频率均处于低阶范围,应注意避免与泵源发生共振,避免管道的疲劳故障、管道泄漏等安全隐患。本文电动机的转速为1 500 r/min,故得泵源频率fb=n/t=1 500 r/min /60 s=25 Hz。
3 结论
基于铁木辛柯梁理论建立了矿井排水管道系统的动力学模型,基于哈密顿变分原理得到了排水管道的振动微分方程,由有限元方法得出了质量和刚度矩阵,较全面地考虑了模型的适用性,并通过试验验证了模型的有效性。提出了一种煤矿排水管道系统模态分析的方法,首先对管道进行了实验,获得频响函数,通过辨识峰值得到了实验的固有频率。同时利用有限元方法建立了管道有限元模型,得到仿真的频率结果,最后结合实验和仿真验证了所建模型的正确性,得到了管道系统的固有频率和振型。本文研究结果对于煤矿排水管道系统的振动故障研究方面具有指导意义。

