方柱绕流吹气降噪数值研究
郭 昊 康国强 侯强中 刘沛清
(北京航空航天大学陆士嘉实验室(航空气动声学工业和信息化部重点实验室), 北京 10019)
0 引言
起落架噪声是飞机气动噪声中不可忽略的一个重要部分,主要体现在起飞和降落阶段,起落架噪声在整个噪声中占据了主导地位。Zaytsev等人通过对波音777整机的过顶噪声阵列测量,起落架噪声在总噪声中有突出贡献。飞机起落架噪声主要包含了钝体噪声和腔体噪声,钝体绕流中最为典型的便是柱体绕流。
1878年,Strouhal通过研究风吹过棒或线等柱体,第一次科学地研究了离散噪声的产生,即通俗所说的风啸声,发现雷诺数在300~10时,离散噪声的频率与圆柱直径成反比,与来流风速成正比,从而有无量纲频率在0.2~0.22之间。自此之后有许多的学者研究了圆柱绕流的气动噪声产生机理。
1952年,英国科学家Lighthill在研究喷流自由湍流的声激发中,由N-S方程中的连续性方程(1)和动量方程(2)推导出了著名的Lighthill方程(3),也就是如今的气动声学基本方程,声类比方程。

(1)
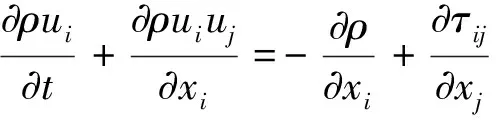
(2)
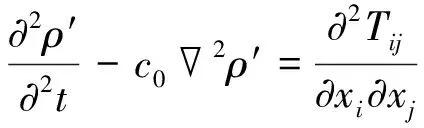
(3)
式中,
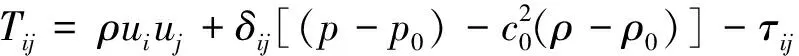
(4)
为Lighthill湍流应力张量,式中三项分别表示由速度导致的雷诺应力、流体黏性导致的黏性应力和热传导的影响。该方程指出了流体动力声源的四极子声源就是流体湍流中变化的应力,并表明了当声场参数不会对流体运动参数产生影响时,可以采用与经典声学理论相似的方法求解,得到声源的声场解,具有实用意义,但是该式未考虑固体边界的影响。
1956年,Phillips在Curle的理论的基础上,推导出了二维柱体(上下加端板或者长细比足够大)的远场纯音声压均方根的计算公式:

(5)
式中,为无量纲频率,=,为展向相关系数,,为柱体表面脉动升力系数,为监测方位角,为监测点到柱体的距离。可以看出,影响二维柱体远场噪声的流动参数主要有三个,分别为表征脱落涡频率的无量纲参数、衡量展向三维效应的,以及体现涡脱落强度的表面脉动升力系数,。
国内,李玲等人通过实验研究了亚临界雷诺数(4.1×10~1.1×10)圆柱绕流气动噪声特性,发现在垂直流向的方向上,圆柱绕流的远场噪声最大,且随着偏离垂向角度的增大,远场噪声逐渐减小,属于典型的偶极子声源特性。并且远场噪声与来流速度的6次方成正比,与监测点到圆柱中心距离的2次方成反比,与Phillips二维柱体纯音噪声预测公式一致。
常见的降低柱体绕流气动噪声的方法可以分为被动控制降噪和主动控制降噪,其中主动控制降噪主要包含了等离子体激励器诱导射流控制和柱体表面吹吸气控制等方法。主动控制方面主要是通过向流场中注入动量,使边界层内流体被加速,以达到延缓分离的效果。
Sohankar等人通过数值模拟方法研究了雷诺数在100~200下通过吹气和吸气控制穿孔在不同入射角(在0~45°)处的涡脱落情况,结果表明,在=150和=45°时在方柱的前侧或后侧施加吹气或吸气为最佳控制情况,在该条件下涡旋脱落得到抑制并且阻力系数减小了约39%。
本文主要通过数值模拟的方法研究了在方柱分离点处施加垂直来流速度方向吹气控制下的气动噪声特性,对零度迎角下三维方柱进行了流场和声场特性研究,包括固定吹气速度3 m/s和固定吹气速度比(吹气速度/来流速度=0.1)的控制条件下改变来流速度大小的情况,探究吹气降噪机理和吹气控制效果。
1 基本算例数值计算
1.1 基本算例计算设置
在三维方柱算例验证的数值计算中,参考LIU Xiaowan等人的相关设置,计算模型选用三维方柱体,如图1所示,方柱截面尺寸为D=0.041 m(高),B=0.043 1 m(宽),以及展向尺寸=4D。数值计算网格划分如图2所示,流向(X)计算域大小取为=30D,其中方柱中心距上游入口边界的距离为10D,距下游出口边界的距离为20D;垂直流向(Y)的计算域大小取为=20D,其中方柱中心距上下边界的距离均为10D。Sohankar等人研究了X-Y平面内计算域大小对计算结果的影响,发现=24D且=16D的计算域足以获得合理的结果。Trias等人研究了柱体在=2.2×10时的翼展方向两点相关性,发现相关性值在小于=2D处下降为零,这表明展向计算域大小为4D足以允许应用周期性边界条件。在本次研究中,沿翼展方向选择了=4D的长度,该长度已在以前的大多数数值研究中使用。
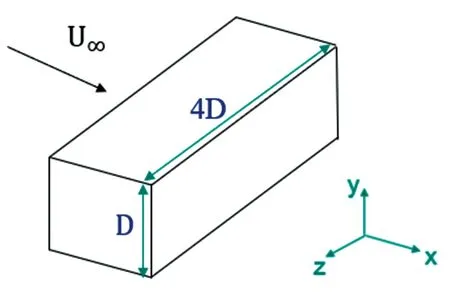
图1 三维方柱计算模型

图2 网格划分
网格划分采用的软件ANSYS ICEM,数值计算采用的软件为ANSYS Fluent version.18,湍流模型选用DDES-SA。方柱表面第一层网格高度严格保证y≤1,近壁面网格增长率为1.1,远场网格增长率为1.2。求解器设置:压力基求解器,非定常数值计算,采用Simple算法对速度-压力耦合项进行求解,时间离散为二阶隐式格式。边界条件设置:1)速度入口;2)压力出口,3)上下面为对称边界条件,4)壁面为无滑移物面。计算参数设置:来流速度30 m/s,雷诺数=8.2×10,气体设置为不可压气体。声场计算:ANSYS Fluent中的FW-H声学计算,声源辐射面为方柱壁面。噪声监测点与LIU Xiaowan等人的实验设置一致,为垂直来流方向在Z=0.082平面与方柱中心距离1.18 m的位置。计算选取的时间步长为5×10s,采样时长为1.05 s,对应大约为100个脱落涡周期。所有设置及参数如图3所示。
对于力系数等计算公式为:

其中,可以为、、,、,、等,为参考面积,和分别为来流密度与来流速度。

图3 计算设置及参数
1.2 网格验证
网格无关验证首先选择展向网格数量进行验证,如图2所示N为展向网格数量,分别取展向网格数量N=32,54,82,108,162。进行流场和声场计算,得到相关流动参数对比,如表1所示,并与相关文献的计算或实验数据进行对比。其中为方柱阻力系数,为脱落涡无量纲频率。从表2中可以看出,当展向网格数量增加到82时,阻力系数收敛,当展向网格数量增加到54时,数收敛,遂认为展向网格在N=82时趋于收敛。

表1 不同展向网格方柱气动参数计算结果
图4和图5为不同展向网格下沿方柱中面(Z=0.082)表面一周的压力系数分布和不同展向网格下方柱尾迹中线时均流向速度分布,可以看出当N=82时计算结果中压力系数分布和方柱尾迹中线相对流向速度与文献[8]计算结果和实验数据较为一致。
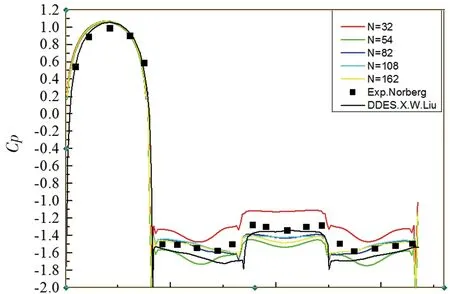
图4 Z=0.082平面不同展向网格沿方柱表面压力系数分布

图5 Z=0.082平面不同展向网格尾迹中线时均流向速度分布
如图6所示为升力脉动的功率谱密度,结果表明,展向网格数量的变化对方柱涡脱落的频率和离散峰强度的影响较小,在N=82时和LIU Xiaowan等人的结果更为接近。
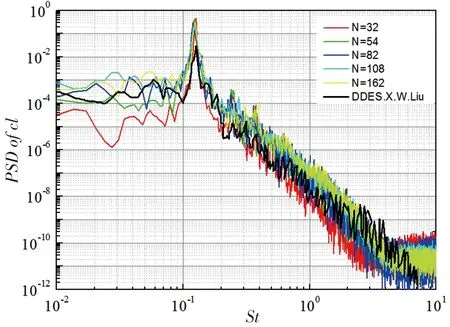
图6 不同展向网格方柱升力脉动PSD
接下来对数值计算中三维方柱的整体网格数量进行收敛性验证,分别取网格数量为2M、4M、6M以及8.5M,进行流场和声场计算,得到相关流动参数对比,如表2所示,并与相关文献的计算或实验数据进行对比。其中为方柱阻力系数,为脱落涡无量纲频率。结果表明,整体网格数量的增加对方柱涡脱落无量纲频率几乎没有影响,但是方柱阻力系数却呈递减的趋势,且网格数量增大到4M后,这个递减的速度减缓了,且与文献[8]中的结果较为一致。
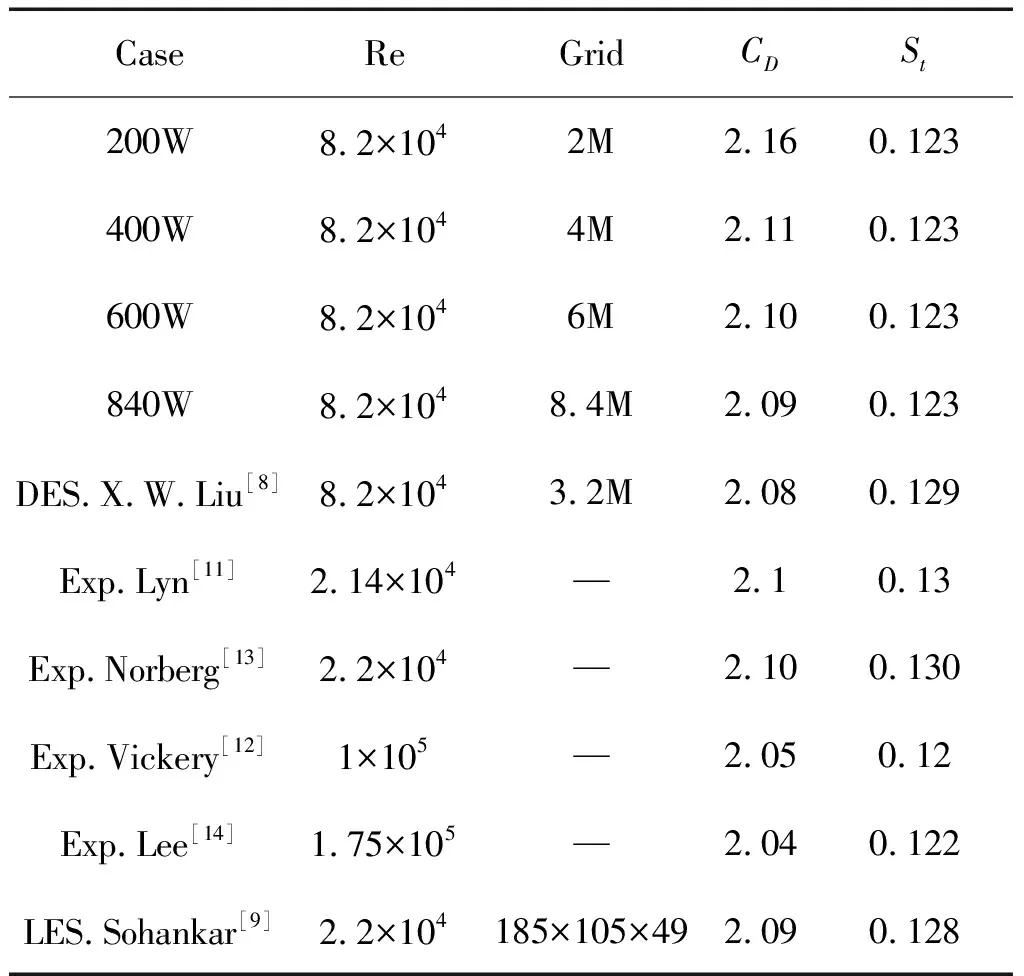
表2 不同网格规模方柱气动参数计算结果
图7展现了不同网格数量下方柱升力脉动功率谱密度,图中不同网格数量对应的功率谱密度的主峰频率和强度几乎一致,表明整体网格的变化对方柱涡脱落的频率和离散峰强度的影响都很小。

图7 不同网格数量下方柱升力脉动PSD
1.3 基本算例验证
对展向网格数量N=82,整体网格数量为6M,湍流模型为DDES S-A的算例进行进一步的验证。表3展示了算例结果气动参数与文献对比结果,可以看出,验证算例计算结果中的阻力系数,升力脉动系数,,阻力脉动系数,和斯特劳哈尔数均与所列文献结果较为一致,说明算例计算结果可以较为正确地反应方柱涡脱落的频率和强度情况。
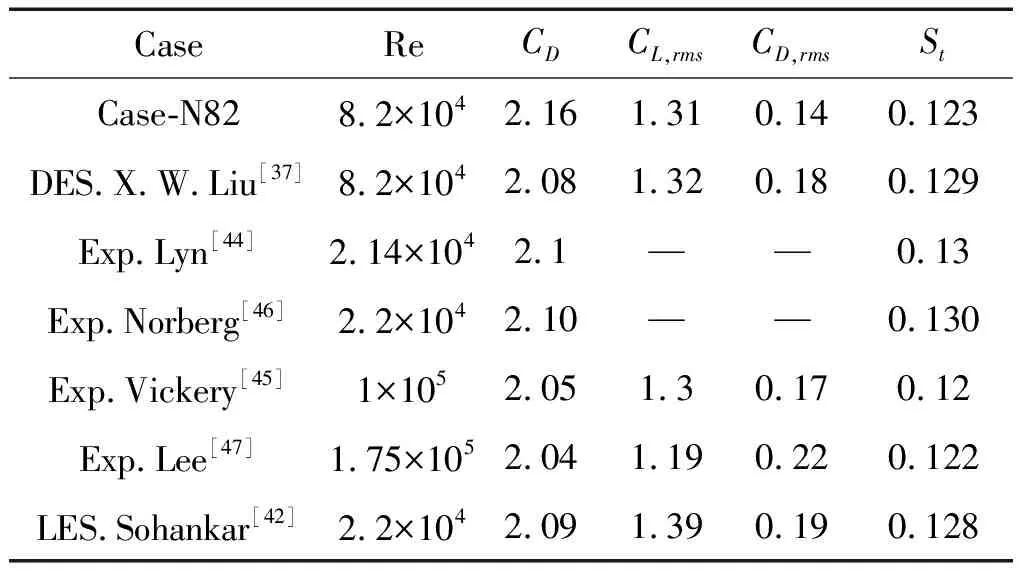
表3 算例气动参数结果
图8展现了-平面内沿方柱表面一周压力系数分布,其中-平面为=0.082处的平面,可以看出沿方柱表面一周压力系数分布计算结果与文献[8]和文献[13]的实验吻合得较好。
图9~图11分别展示了=0082的-平面内方柱尾迹中线时均流向速度、尾迹中线的流向速度脉动和横向速度脉动,通过比较=0的位置可以看出尾迹回流区的大小,结果表明蓝线所示的尾迹回流区大小与黑线所示的结果是一致的。图9中,在=15附近流向速度脉动偏低,横向速度脉动偏高,在2<<5处横向速度脉动结果与实验结果贴合得较好。

图8 Z=0.082平面方柱表面一周压力系数分布

图9 Z=0.082平面尾迹中线时均流向速度分布
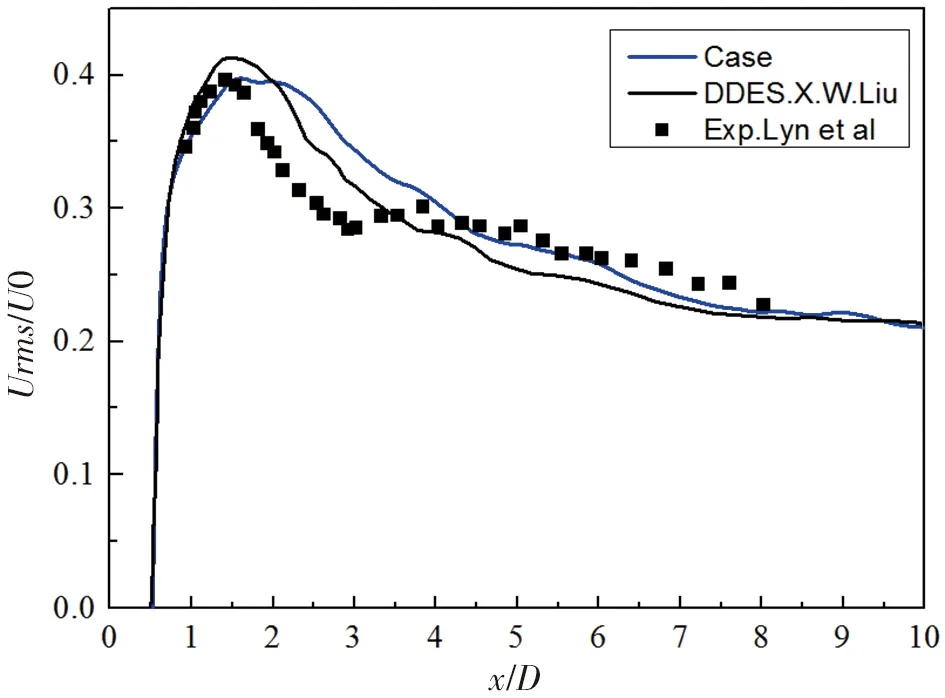
图10 Z=0.082平面尾迹中线流向速度脉动

图11 Z=0.082平面尾迹中线横向速度脉动
图12展现了=0082处-平面内时均流线图对比(图12(a)为计算结果,图12(b)为对比文献[8]的结果),结果表明较为一致。

(a) N=82在Z=0.082平面时均流线

(b) LIU Xiaowan[8]等人计算结果在Z=0.082平面时均流线图12 时均流线对比
图13展现了方柱远场噪声频谱图对比,声学监测点设置在与来流垂直的方向上,与方柱中心距离为1.18 m,黑线为算例计算结果,红线为两端带端板的方柱实验结果,从远场监测的SPL图可以得出,计算结果和实验较为吻合。

图13 Z=0.082平面垂直流向1.18 m处方柱远场噪声频谱图对比
2 三维无限长方柱吹气控制
2.1 吹气方式与计算工况
计算边长为D=0.03 m的三维方柱模型,其展向长度为L=4D,包括来流速度分别为30 m/s、40 m/s、50 m/s和60 m/s下的干净构型、吹气速度为3 m/s的构型和吹气速度为0.1的构型。其中,吹气位置为方柱前缘分离点处,进行垂直来流方向吹气,吹气速度为,吹气口的大小为宽1.5 mm,为方柱直径的1/20,长与展长一致,为4D,如图14所示。展向网格数量N=82,整体网格数量为6M,计算中噪声监测点布置在垂直来流方向,远场噪声监测点与方柱中心距离2.2 m,近场噪声监测点与方柱中心距离0.09 m。图15展示了吹气工况。

图14 三维方柱吹气模型与吹气示意图
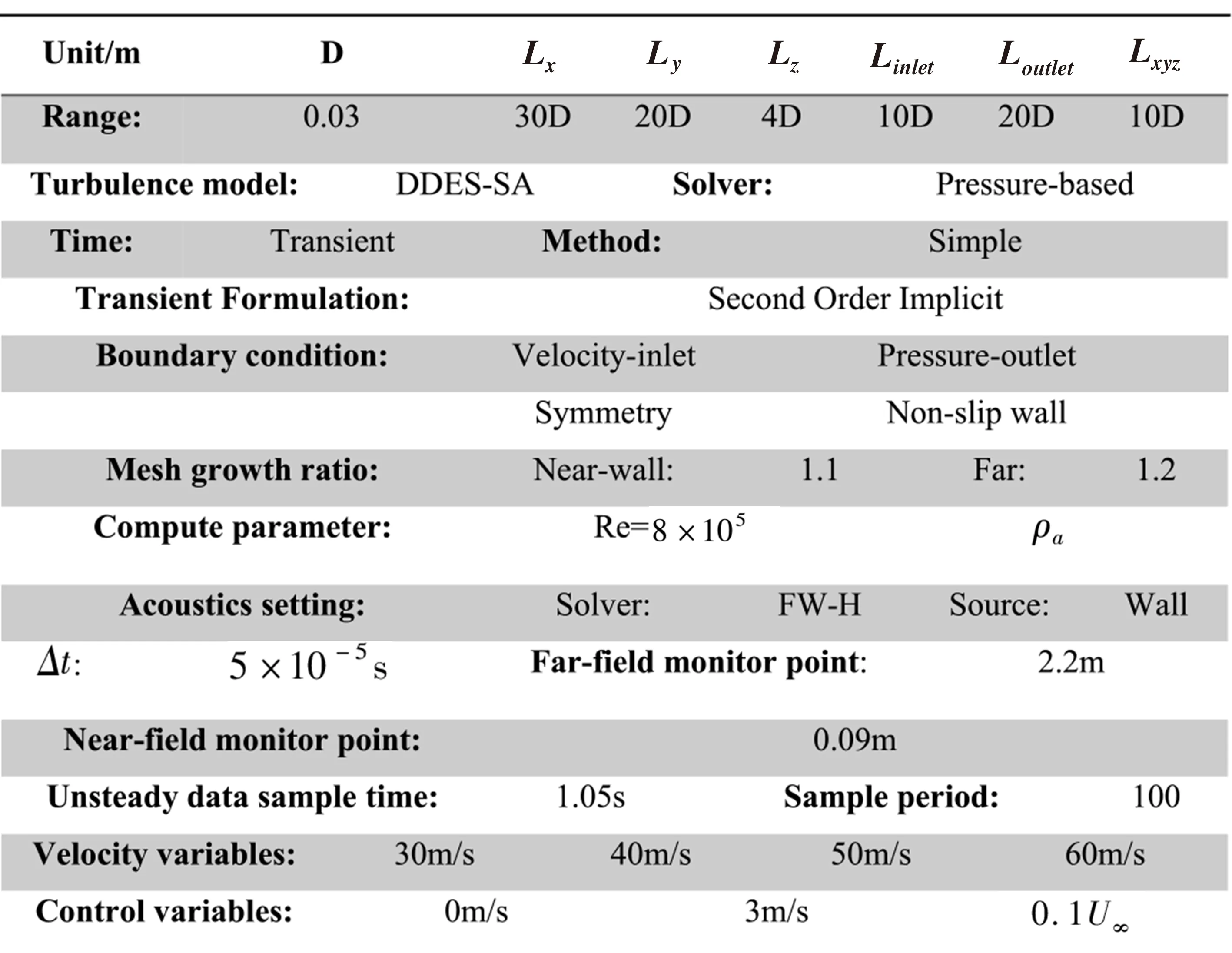
图15 吹气工况设置
2.2 固定吹气速度降噪
针对固定吹气速度的方法对三维方柱进行吹气控制,在方柱前缘分离点处分别向两侧施加3 m/s的吹气控制,向流场注入动量。保持吹气速度不变,来流速度从30 m/s以增长间隔10 m/s增长到60 m/s,对比吹气控制效果的变化。
表4展现了三维方柱在无吹气构型和吹气速度为3 m/s的构型在来流速度分别为30 m/s、40 m/s、50 m/s和60 m/s时的气动参数计算结果,施加吹气和改变来流速度都对脱落涡无量纲频率几乎没有影响,这是由于方柱分离点固定,脱落频率对雷诺数并不敏感。

表4 三维无限长方柱气动参数计算结果
图16展现了方柱在固定吹气速度3 m/s下的升力脉动系数和阻力脉动系数对比图,可以看出施加吹气控制后,升力脉动系数和阻力脉动系数都较明显地降低。在无吹气时方柱升力脉动系数几乎不随来流速度变化,而在来流速度为30 m/s时施加吹气控制后升力脉动几乎下降到了无吹气结果的二分之一处,而随着来流速度的增加,升力脉动呈现出递增的趋势,逐渐接近无吹气状态。
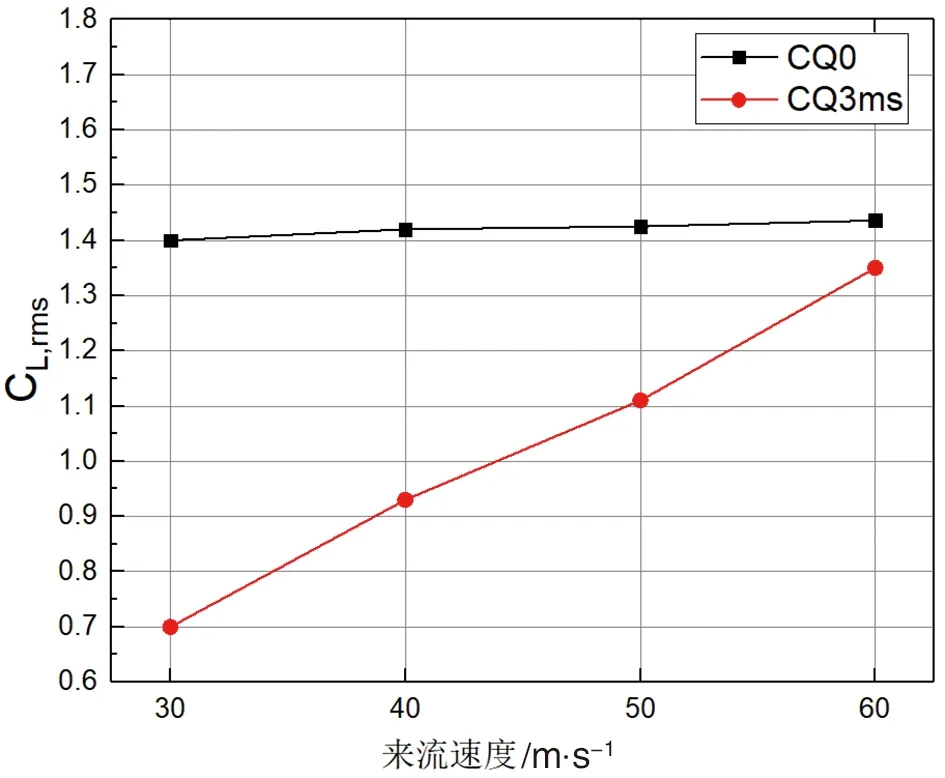
(a) 升力脉动系数
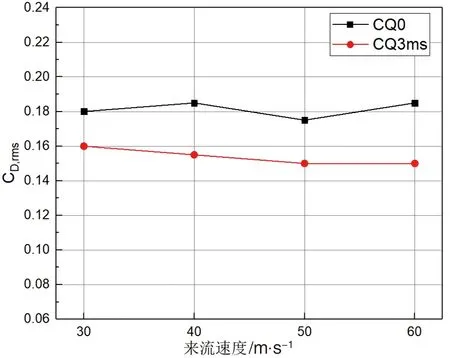
(b) 阻力脉动系数图16 无吹气与固定吹气速度3 m/s控制的方柱绕流升力与阻力脉动系数对比
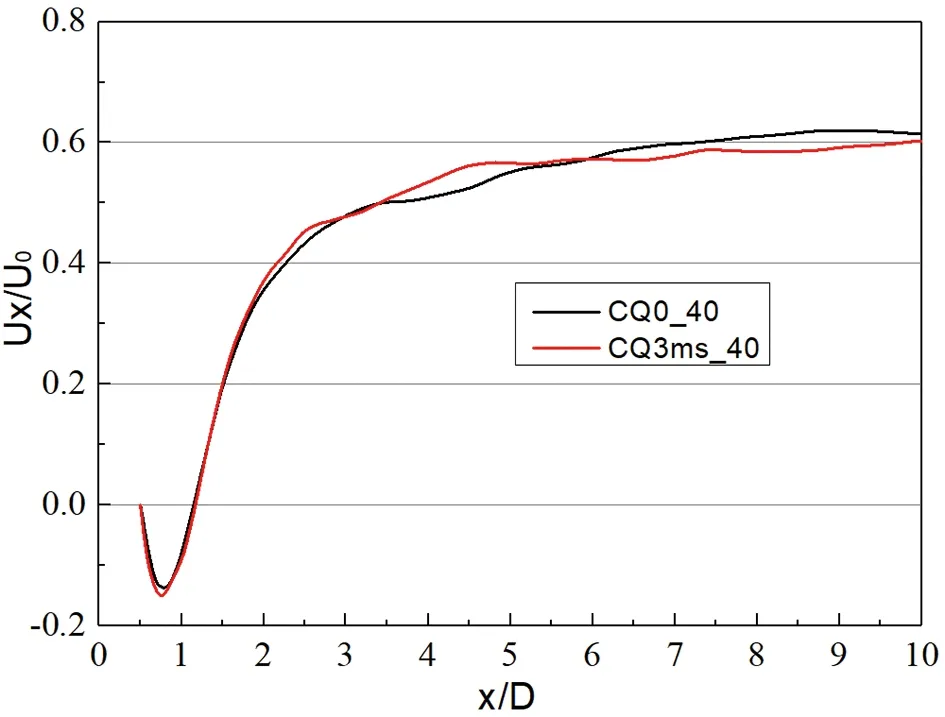
图17展现了不同来流速度下方柱尾迹中线时均流向速度曲线图,其中横坐标为0的位置为方柱几何模型的中心。对比相同来流速度下有无吹气构型的结果,通过流向速度为0的位置可以判断出方柱尾迹回流区的大小:在来流速度为30 m/s时施加3 m/s速度的吹气控制后,方柱尾迹回流区会变小,而来流速度增加后,方柱尾迹回流区的变化减小了,即来流速度增加后吹气控制的效果减弱。

(a) 30 m/s
(b) 40 m/s

(c) 50 m/s
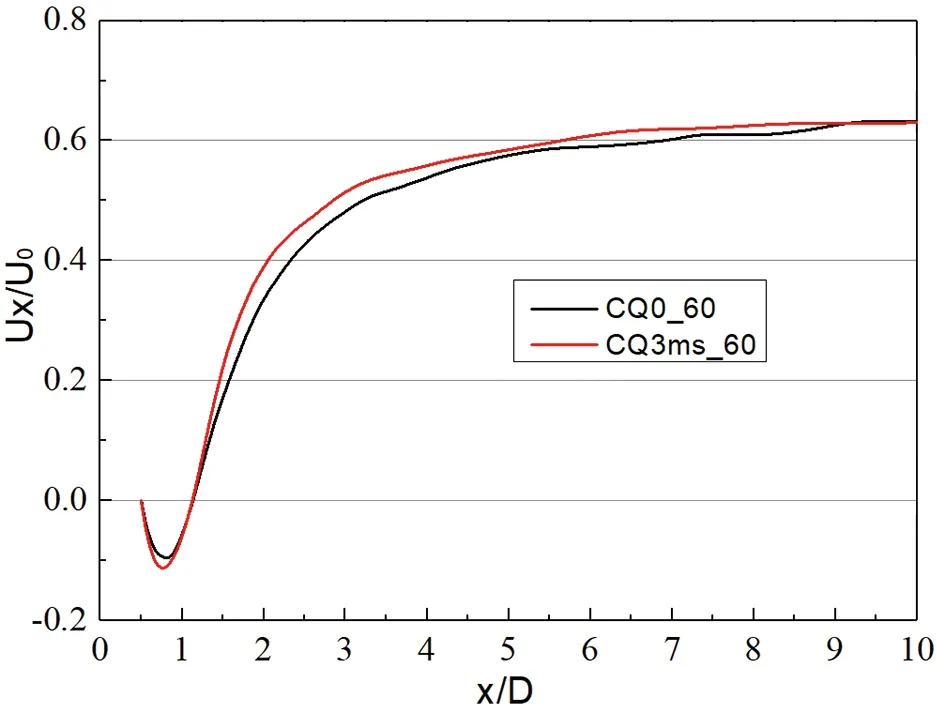
(d) 60 m/s图17 不同来流速度方柱在Z=0.082平面尾迹中线时均流向速度
图18展现了不同来流速度下方柱绕流远场PSD,离散峰出现在=0.12处,对应方柱的卡门涡脱。黑线为无吹气构型计算结果,红线为3 m/s吹气的计算结果,对比相同来流速度下两者的远场噪声PSD可以看出,施加吹气控制后,原本非常强的离散峰得到了一定程度的减弱,主峰处的离散声有4.2 dB~9.5 dB的降低,并且在主峰频率附近区域也有一定程度的降低。对比不同来流速度下的结果可以看出,当来流速度增大后,降噪效果明显减弱。
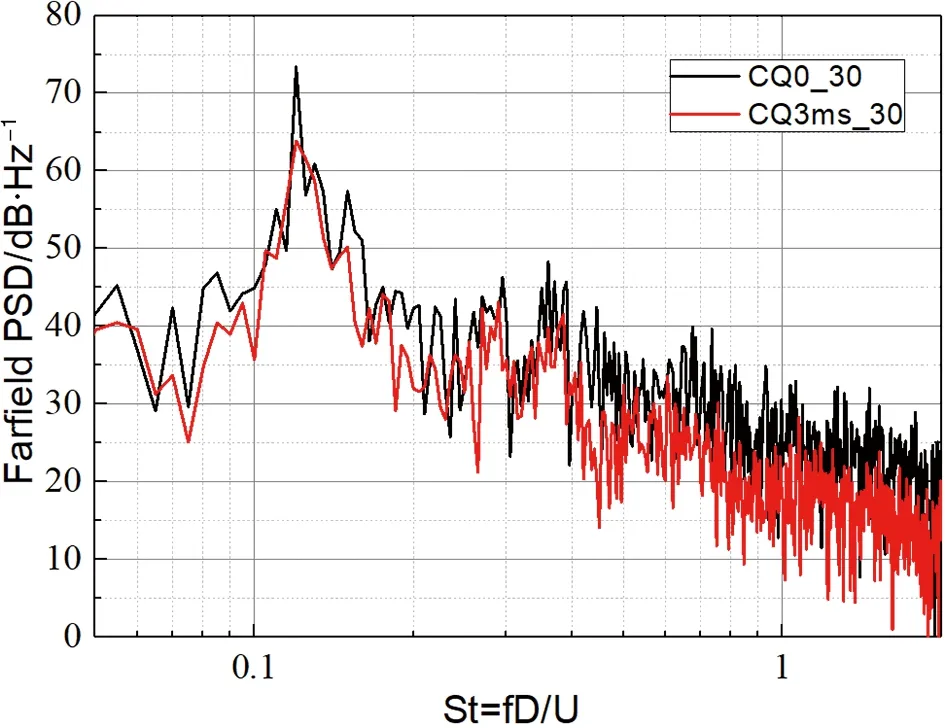
(a) 30 m/s

(b) 40 m/s

(c) 50 m/s
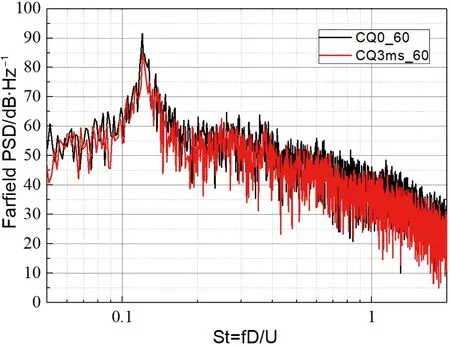
(d) 60 m/s
图19展现了不同来流速度下方柱绕流近场PSD,离散峰出现在=0.12处。黑线为无吹气构型计算结果,红线3 m/s吹气的计算结果,施加吹气控制后,主峰处的离散声有5 dB~12 dB的降低,并且在主峰频率附近区域也有一定程度的降低。但是近场噪声所展现出来的降噪效果随着来流速度的改变,并没有在频谱图中有较为直观的改变。

(a) 30 m/s

(b) 40 m/s
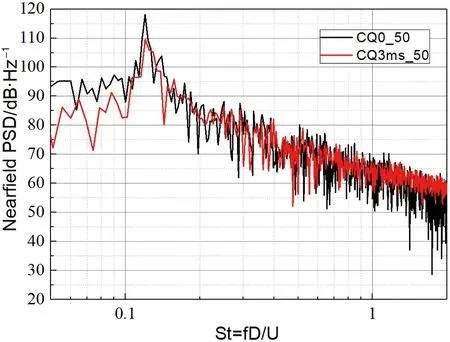
(c) 50 m/s

(d) 60 m/s

(a) 远场总声压级
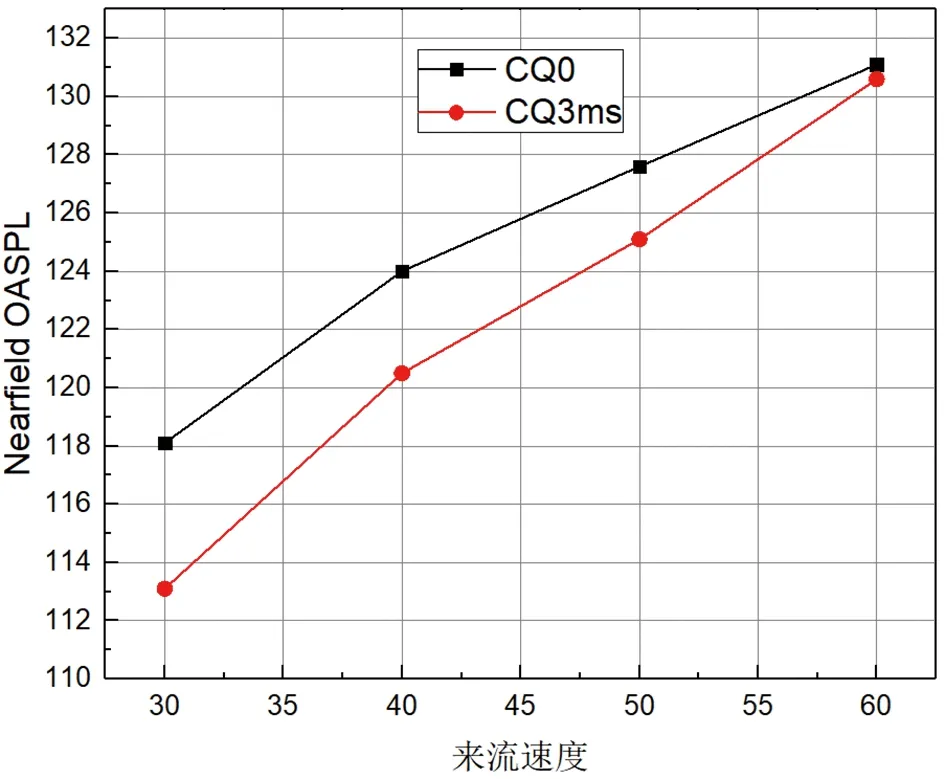
(b) 近场总声压级
图20展现了方柱远场噪声和近场噪声的总声压级,可以看出随着来流速度的增加,总声压级呈现出递增的趋势。对比图中无吹气结果和吹气3 m/s结果,在来流速度为30 m/s时总声压级有6 dB左右的降低,随着来流速度的增加,降噪效果逐渐减弱,当来流速度增大到60 m/s时,降噪效果几乎为零。
2.2 固定吹气比降噪
用固定吹气速度比的方法对三维方柱进行吹气控制,在方柱前缘分离点处分别向两侧施加0.1倍来流速度的吹气控制,向流场注入动量。保持吹气速度比不变,即吹气速度为来流速度的十分之一,并在来流速度从30 m/s以增长间隔10 m/s增长到60 m/s下,对比吹气控制效果的变化。
表5展现了三维方柱在无吹气构型和吹气速度为0.1的构型在来流速度分别为30 m/s、40 m/s、50 m/s和60 m/s时的气动参数计算结果。
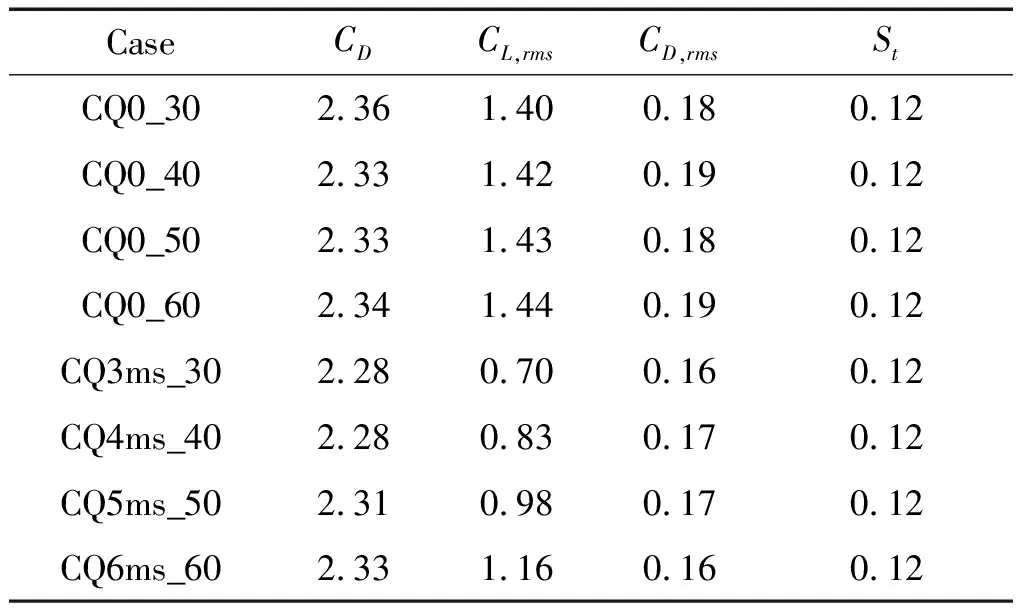
表5 固定吹气比三维方柱气动参数计算结果
图21展现了方柱升力和阻力脉动系数对比图,可以看出施加吹气控制后,升力和阻力脉动系数都较明显地降低。与固定3 m/s吹气速度的结果相比,施加0.1倍来流速度大小的吹气速度后的升力脉动系数随来流速度增长的幅度要小很多,说明在相同来流速度下,增加吹气速度是可以增大控制效果的。

(a) 升力脉动系数

(b) 阻力脉动系数图21 无吹气与固定吹气比控制的方柱绕流升力与阻力脉动系数对比
图22展现了不同来流速度下方柱在=0.082平面尾迹中线时均流向速度曲线图,其中横坐标为0的位置为方柱几何模型的中心。对比相同来流速度下有无吹气构型的结果,通过速度为0的位置可以判断出方柱尾迹回流区的大小,可以明显看出,在方柱前缘分离点处施加十分之一来流速度大小的吹气控制后,方柱尾迹回流区会变小,在来流速度为30 m/s时最明显,而来流速度增加后,方柱尾迹回流区的变化减小了,说明来流速度增加后吹气控制的效果减弱了。

(a) 30 m/s

(b) 40 m/s
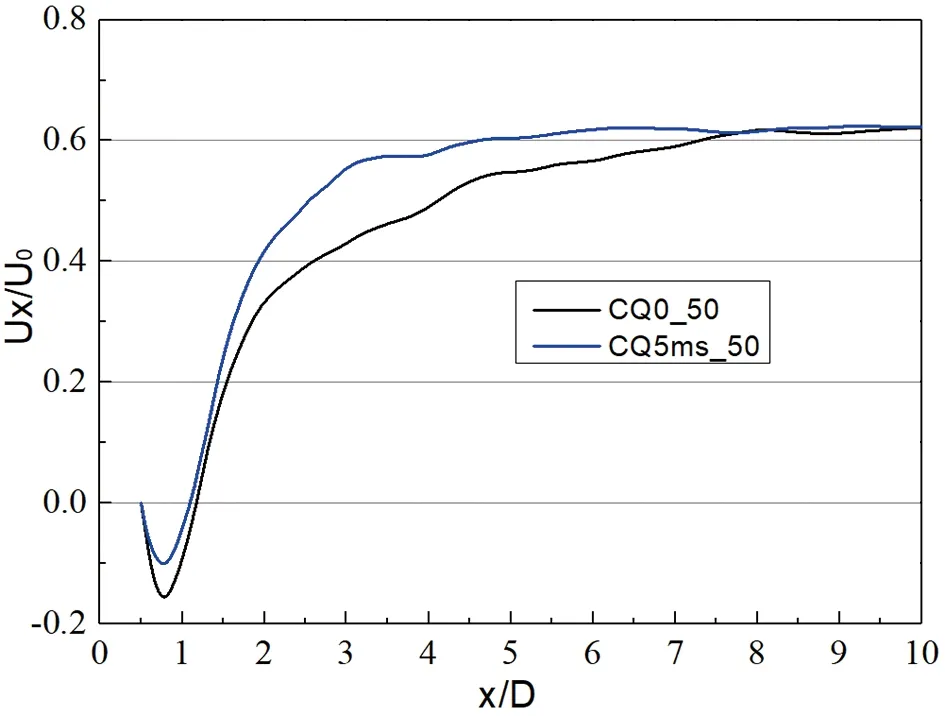
(c) 50 m/s
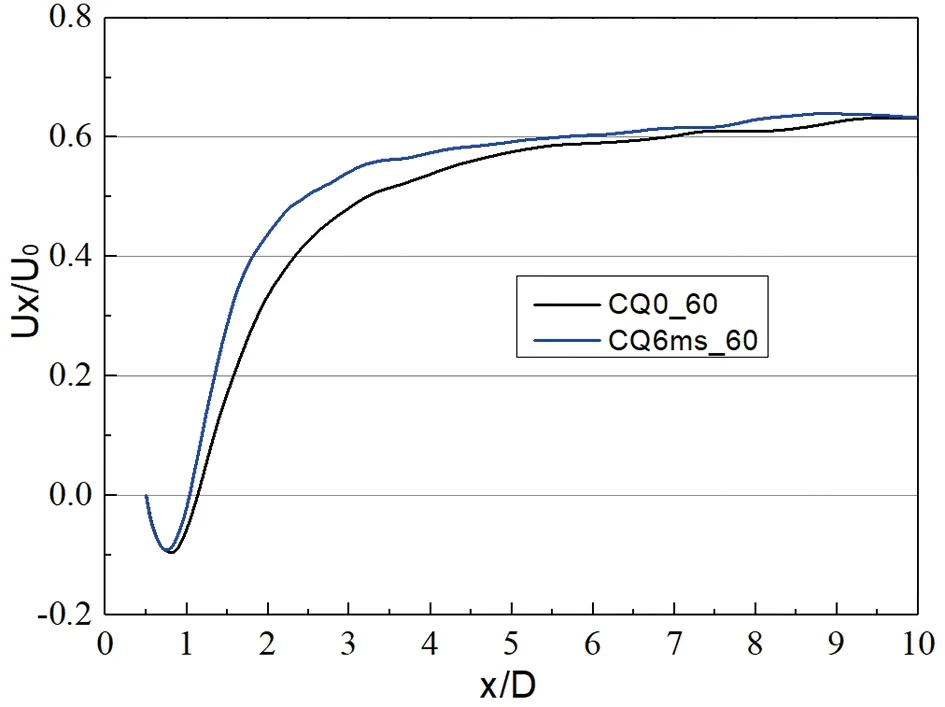
(d) 60 m/s图22 不同来流速度下方柱在Z=0.082平面尾迹中线时均流向速度
图23展现了不同来流速度下方柱绕流远场PSD,离散峰出现在=0.12处。黑线为无吹气构型计算结果,蓝线为施加0.1吹气速度的计算结果,对比相同来流速度下两者的远场PSD可以看出,施加吹气控制后,主峰处的离散声有5 dB~9.5 dB的降低,并且在主峰频率附近区域也有一定程度的降低。对比不同来流速度下的结果可以看出,当来流速度增大后,降噪效果明显减弱。

(a) 30 m/s

(b) 40 m/s

(c) 50 m/s

(d) 60 m/s图23 不同来流速度下方柱绕流远场PSD
图24展现了不同来流速度下方柱绕流近场气动噪声频谱图,离散峰出现在=0.12处。黑线为无吹气构型计算结果,蓝线为施加0.1吹气速度的计算结果,对比相同来流速度下两者的近场噪声频谱图可以看出,施加吹气控制后,主峰处的离散声有8.2 dB左右的降低,并且在主峰频率附近区域也有一定程度的降低。但是近场噪声所展现出来的降噪效果随着来流速度的改变,并没有在频谱图中有较为直观的改变。

(a) 30 m/s
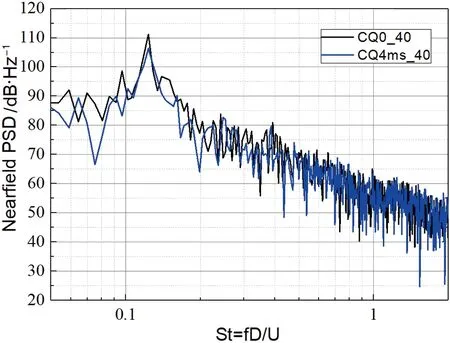
(b) 40 m/s

(c) 50 m/s
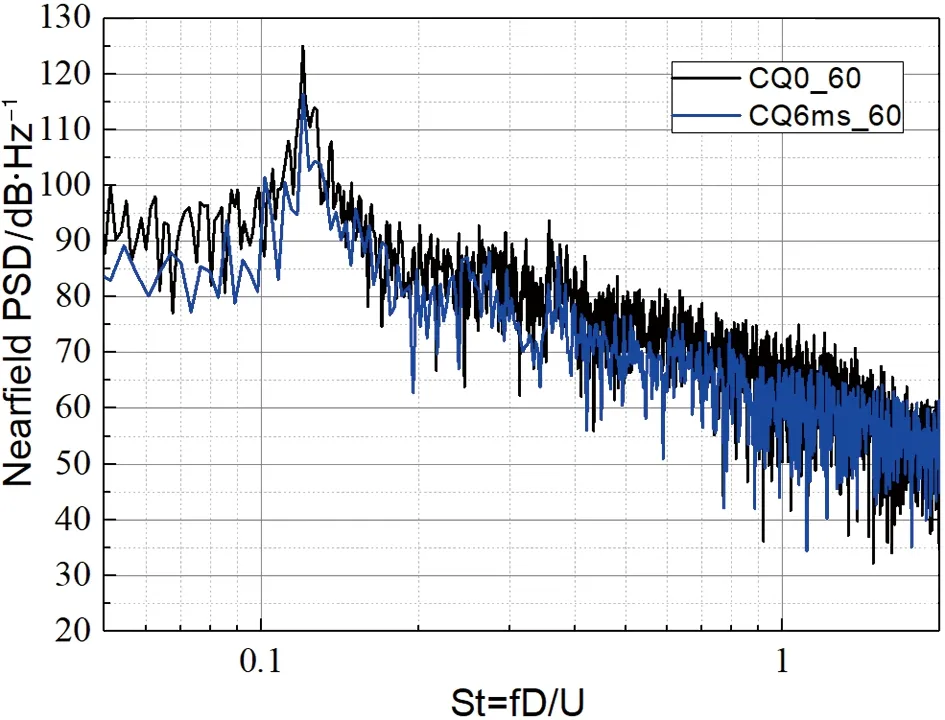
(d) 60 m/s图24 不同来流速度下方柱绕流近场PSD
图25展现了方柱远场噪声和近场噪声的总声压级,可以看出随着来流速度的增加,总声压级呈现出递增的趋势,对比图中无吹气结果和吹气0.1的结果可以发现,在来流速度为30 m/s时总声压级有6 dB左右的降低。与吹气3 m/s的结果相比,吹气0.1倍来流速度所展现的降噪效果更好,在来流速度为60 m/s时仍然有接近2 dB的降噪效果,如图26所示。

(a) 远场总声压级
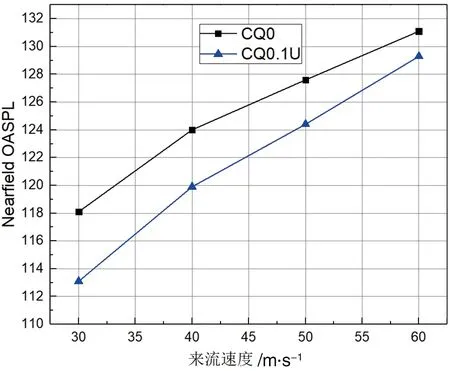
(b) 近场总声压级图25 无吹气与固定吹气比近远场总声压级对比
3 结论
吹气控制对方柱绕流的柱体噪声有一定的控制效果。
1) 吹气控制可使方柱阻力系数减小,升力脉动系数,降低,脱落涡频率几乎不改变,尾迹回流区减小;
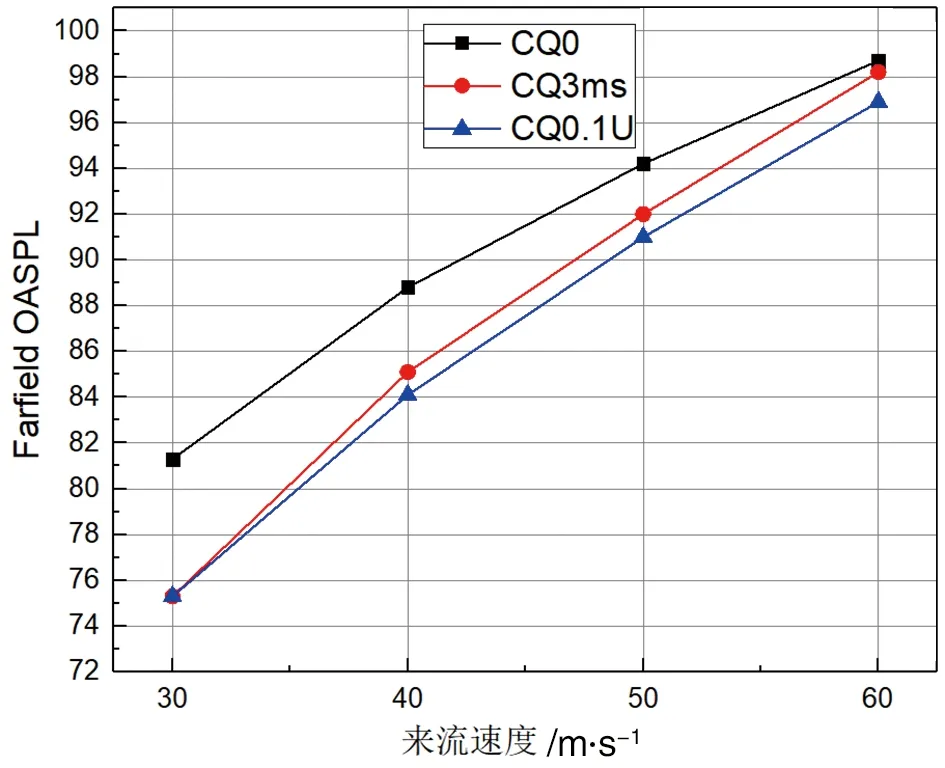
(a) 远场总声压级
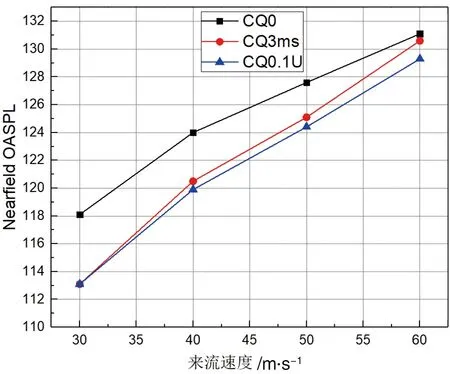
(b) 近场总声压级图26 无吹气、固定吹气速度与固定吹气比近远场总声压级对比
2) 吹气控制对小速度情况(30 m/s)的降噪更有效果,升力脉动系数,降低为无吹气控制的一半;
3) 通过在固定吹气速度和固定吹气速度比控制效果对比,可以知道越大的吹气速度对柱体绕流噪声降噪更有效果。

