管箱结构对挠性管板一次应力影响的研究
高欢,唐辉永,徐儒庸,岳国印,李小梅,孟令冰
(中国寰球工程有限公司北京分公司,北京 100012)
挠性管板结构早期主要应用在甲醇、合成氨、制氢和硫回收等石油化工装置中的余热锅炉上[1],近年来随着国内乙烯装置的不断增多,挠性管板结构也被应用在乙烯装置中的换热器上,克服了常规刚性厚管板因刚性过大热膨胀后变形不协调导致换热管与管板焊接接头容易泄漏的问题,主要是因为挠性管板厚度较薄,具有一定的柔性,能够吸收管壳程之间的热膨胀差,减小热应力[2]。除此之外,挠性管板结构还具有能提高传热效率、节省材料等优点。
常规的挠性管板设计方法已经被列入国标GB/T 151—2014《热交换器》附录中,但对适用范围作了严格限制[3],已有案例的设计条件往往都超出该范围,需要采用较复杂的有限元分析设计方法。这说明挠性管板结构虽然已经成功应用在一些设备上,但依然不够成熟,距离能够全面普及和推广还有很长一段路要走,也从侧面反映出目前对挠性管板的研究还不够彻底。近年来,国内学者针对挠性管板的结构设计和强度计算做了一些研究工作,但研究内容往往着眼于管板的厚度或者挠性过渡段半径Rs[4-8]等方面,尚未有学者研究过管箱结构对挠性管板一次应力的影响。本文采用有限元分析方法,以某挠性管板为基本结构,研究不同管箱结构对挠性管板一次应力的影响,总结规律,为挠性管板结构的进一步优化和推广应用打下基础。
1 挠性管板基本参数
挠性管板的基本参数如表1 所示。
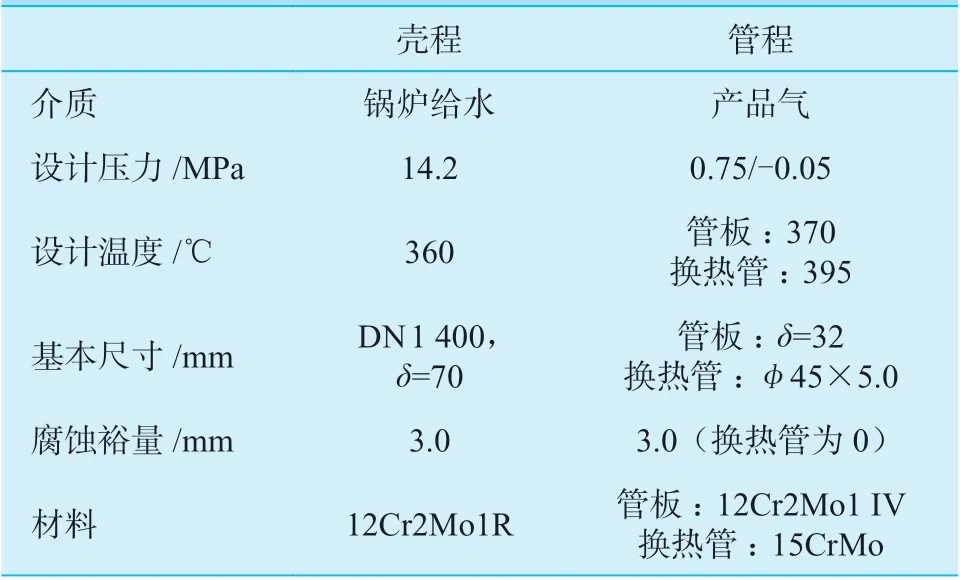
表1 挠性管板基本参数Table 1 Basic parameters of the flexible tubesheet
2 计算方法
一次应力,在分析设计标准JB 4732—1995(2005年确认版)中的定义为:“为平衡压力与其他机械载荷所必须的法向应力或剪应力”[9]。一次应力对容器失效影响最大,是维持结构各部分平衡直接需要的,无此应力结构就会发生破坏[10]。一次应力的特点是没有自限性,所以挠性管板在压力作用下产生的一次应力必须小于其许用值,如不满足则会引起管板过量的总体塑性变形而造成结构破坏。
实际结构中,挠性管板不是独立存在的,而是与壳程筒体、管箱及换热管等直接相连,在压力作用下挠性管板会与这些结构产生变形协调,从而产生二次应力。如果有限元分析模型包括壳程筒体、管箱和换热管等结构,则最终的应力结果会同时包含一次应力和二次应力。二次应力会增大或减小挠性管板的总应力强度,通过应力分类的方法区分出一次应力也是不可能的。因此,为了计算得到挠性管板的一次应力,有限元分析模型需要将壳程筒体、管箱和换热管等结构去除,但为了施加挠性管板壳程侧的边界约束条件,壳程筒体和换热管仍然需要保留一小段,施加压力载荷时只施加在管板两个侧面上,如此一来,最大程度上将二次应力所占的比重减小,使得管板的应力成分主要为一次应力。
3 初始研究
3.1 模型简介
根据结构的对称特点,取挠性管板垂直对称面一侧的1/2 进行分析。为了研究管箱结构对挠性管板一次应力的影响,首先分三种模型进行对比:(1)模型A,包括挠性管板、部分壳程筒体和换热管,其中挠性管板的管程侧齐平,无多余结构;(2)模型B,包括挠性管板、部分壳程筒体和换热管,其中挠性管板带有一个法兰环结构;(3)模型C,同样包括挠性管板、部分壳程筒体和换热管,其中挠性管板管程侧有厚度为30 mm,长度为50 mm 的翻边结构。三种初始模型具体的尺寸及几何模型如图1 ~ 6 所示。模型A 的这种挠性管板结构在实际中是不存在的,因为其无法与管箱进行连接,在此仅为了与其他两个模型作对比用;模型B 的挠性管板带法兰环,可以通过螺栓与管箱法兰连接;模型C 的挠性管板则通过管程侧翻边与管箱筒体直接焊接相连。
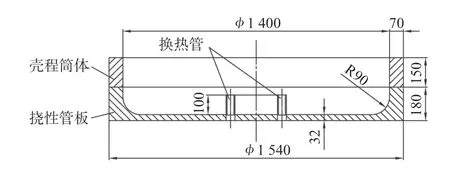
图1 模型A 尺寸示意图Fig.1 Schematic plot of dimensions of model A
模型划分网格时均采用8 节点Solid185 实体单元,管板平板部分沿厚度方向划分为四层网格,模型有足够高的网格密度以保证计算结果的准确性。三种模型的网格密度相同,其分析结果具有可对比性,由于篇幅限制,在此以模型C 为例进行说明,如图7 所示。模型的载荷加载及边界条件设置方面:(1)挠性管板两侧面施加压力载荷,壳程侧表面为14.2 MPa,管程侧表面为-0.05 MPa,其他结构不施加压力载荷;(2)壳程筒体端面和换热管端面施加轴向约束,模型对称面施加对称约束。三种模型的加载和约束方式相同,在此也以模型C 为例进行说明,如图8 所示。
图2 模型A 几何模型Fig.2 Geometric model of model A
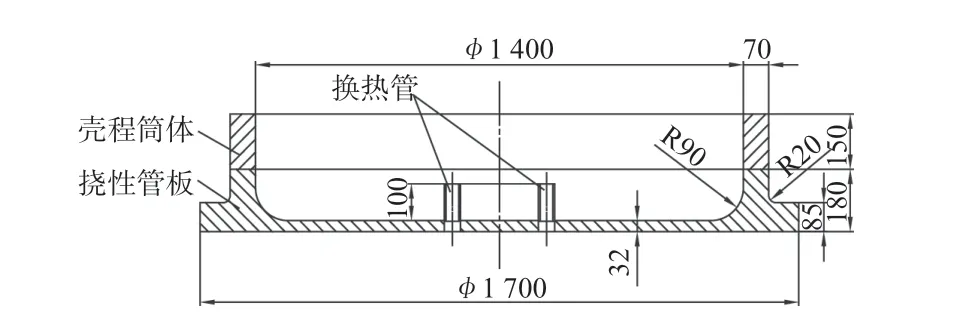
图3 模型B 尺寸示意图Fig.3 Schematic plot of dimensions of model B
图4 模型B 几何模型Fig.4 Geometric model of model B

图7 模型C 有限元模型Fig.7 Finite element model of model C

图8 模型C 加载及边界条件设置Fig.8 Loading and boundary condition setting of model C
3.2 应力结果及对比分析
经过有限元计算,得到三种模型的应力强度云图,如图9 ~ 11 所示。由图可知,三种挠性管板的管箱结构虽有不同,但应力强度最大点位置相同,均位于布管区周边某一管孔的边缘(壳程侧),且管板上的应力分布情况是一致的:管板布管区部分和挠性过渡段部分的应力强度较低,而过渡段以内的非布管区部分则应力强度较高,说明管箱结构的不同并没有对管板上的应力分布造成太大影响。

图9 模型A 应力强度云图Fig.9 Stress intensity contour of model A
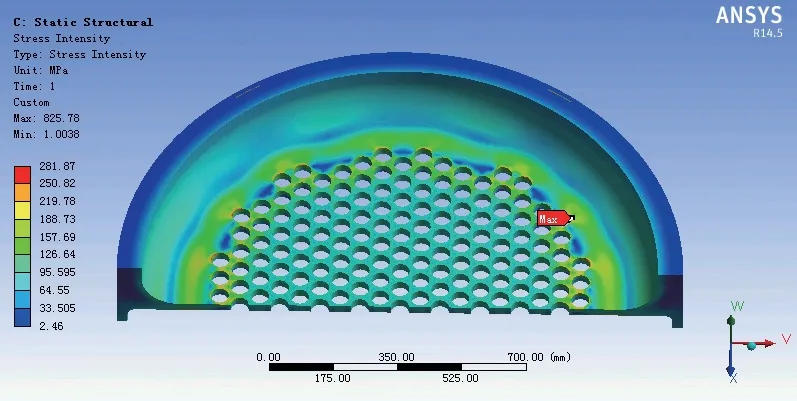
图11 模型C 应力强度云图Fig.11 Stress intensity contour of model C
挠性管板的高应力区往往同时含有一次应力、二次应力和峰值应力等成分,各种应力成分混杂在一起,想要从中区分出一次应力比较困难,而低应力区(即应力强度云图中蓝色部位)则几乎以一次应力成分为主,因此需要在这些低应力区选取路径后,通过应力线性化得到一次应力。按照此原则,在管板的低应力区选取三条路径,如图12 ~ 15 所示,其中路径S-1 通过管板中心部位三根换热管的管桥中心点处,路径S-2 通过布管区周边的最低应力处,路径S-3 通过管板过渡段的最低应力处。三条路径上的应力线性化结果列于表2 中,由于各路径所通过区域的应力以一次应力成分为主,所以应力线性化得到的薄膜应力为一次总体薄膜应力Pm,薄膜加弯曲应力为一次局部薄膜应力加一次弯曲应力PL+Pb。
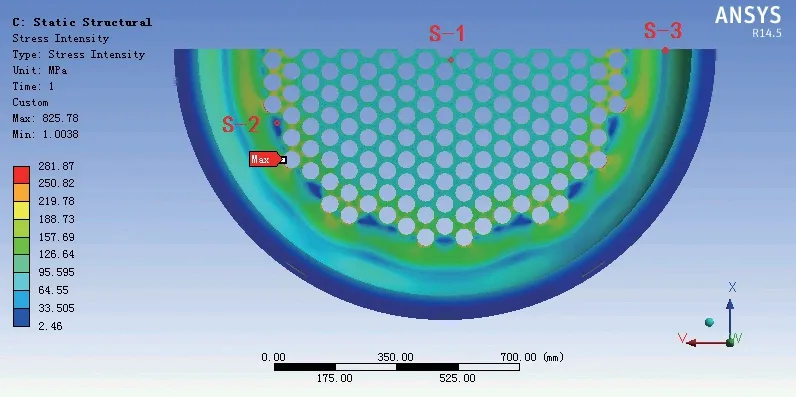
图12 应力线性化路径Fig.12 Stress linearization paths

图13 路径S-1 位置Fig.13 Location of path S-1
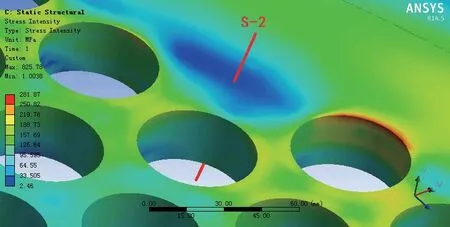
图14 路径S-2 位置Fig.14 Location of path S-2

图15 路径S-3 位置Fig.15 Location of path S-3
由表2 中三个模型的应力结果对比可知,挠性管板在管箱侧增加法兰环或者翻边结构之后,管板上一次应力水平有所降低,尤其以路径S-3 上的PL+Pb应力值降低最为明显,模型B 路径S-3 上的PL+Pb应力值比模型A 降低了17.3%,模型C 路径S-3 上的PL+Pb应力值比模型A 降低了8.1%。法兰环和翻边结构均对管板起到了加强作用,尤其对路径S-3 所在位置即管板挠性过渡段处的加强作用最为明显,且模型B 和模型C 对比可知,法兰环的加强作用稍好,使管板承受壳程内压的能力更强。
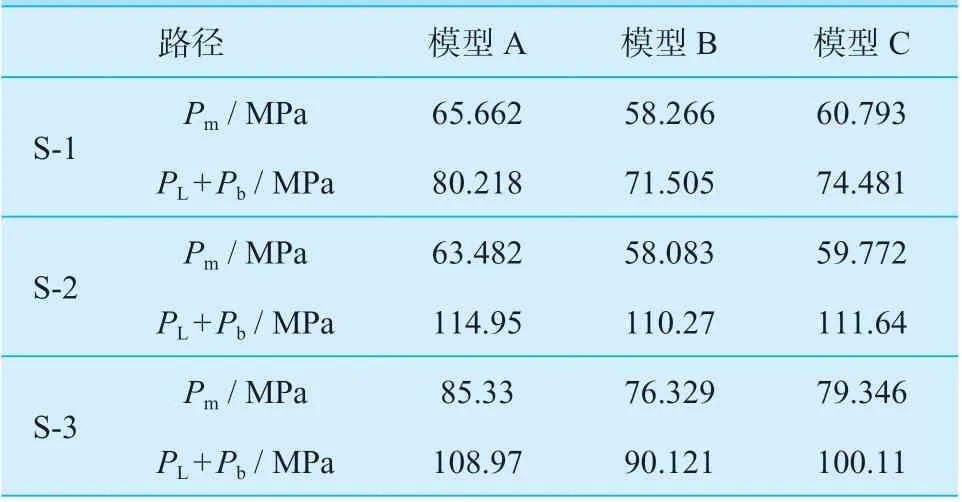
表2 模型A ~ 模型C 的应力线性化结果Table 2 Stress linearization results of model A to model C
模型B 的结构形式类似于GB/T151 标准中“管板延长部分兼做法兰”的结构,管板的法兰环与管箱法兰通过螺栓相连,产生的法兰力矩会传递到管板上,所以该管板除了要承受管、壳两侧的压力、温度载荷、换热管的支撑作用外,还要受到管箱法兰附加力矩的作用,而模型C 则直接通过翻边与管箱焊接相连,没有此附加力矩的作用。对于挠性管板这种复杂的、关键的结构来说,受力越简单越好,因此笔者认为,虽然模型B的法兰环对管板加强作用稍好一些,但模型C 的综合性能更均衡,且节省材料,实用性更强。下文将以模型C 为基础做进一步研究。
4 基于初始模型的进一步研究
4.1 模型简介
首先,为了研究翻边厚度对挠性管板一次应力的影响,在模型C(翻边结构外径与壳程筒体外径对齐,外径均为φ1 540 mm)的基础上继续增加翻边厚度50%、100%,即翻边厚度分别增加到45 mm、60 mm,此二模型分别定义为模型C1 和模型C2;其次,为了研究翻边内径对挠性管板一次应力的影响,增加三个翻边内径与壳程筒体内径对齐的模型(内径φ1 400 mm),其翻边厚度分别为30 mm、45 mm 和60 mm,依次定义为模型C3、模型C4 和模型C5。模型C1 和模型C2 的外形与模型C 相似,可参考图5 和图6,由于篇幅限制不再赘述;模型C3 的尺寸和几何模型如图16 和图17 所示,模型C4 和模型C5 的外形与之相似,也不再赘述。

图5 模型C 尺寸示意图Fig.5 Schematic plot of dimensions of model C

图6 模型C 几何模型Fig.6 Geometric model of model C
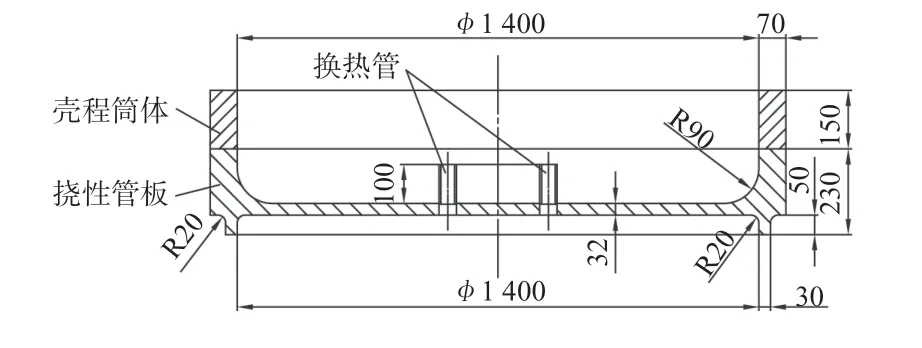
图16 模型C3 尺寸示意图Fig.16 Schematic plot of dimensions of model C3
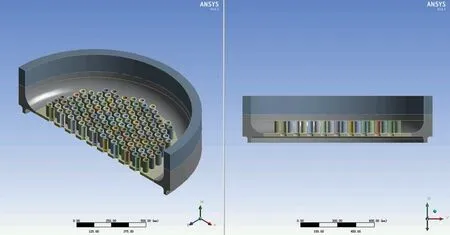
图17 模型C3 几何模型Fig.17 Geometric model of model C3
4.2 应力结果及对比分析
模型C1 ~ 模型C5 的加载和约束方式与上文相同,即挠性管板两侧施加压力,模型上相应位置施加轴向约束和对称约束,经过有限元计算得到五个模型的应力结果,如图18 ~ 22 所示。
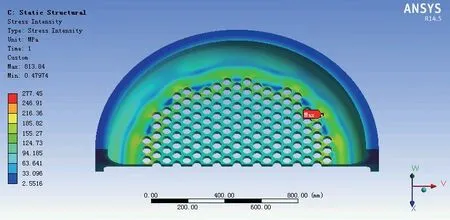
图18 模型C1 应力强度云图Fig.18 Stress intensity contour of model C1
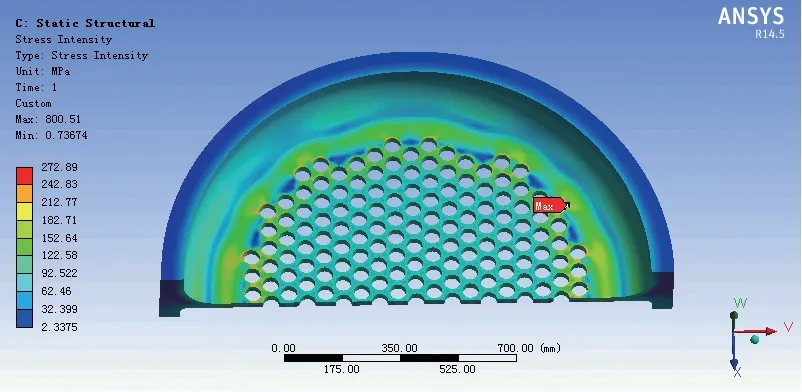
图19 模型C2 应力强度云图Fig.19 Stress intensity contour of model C2
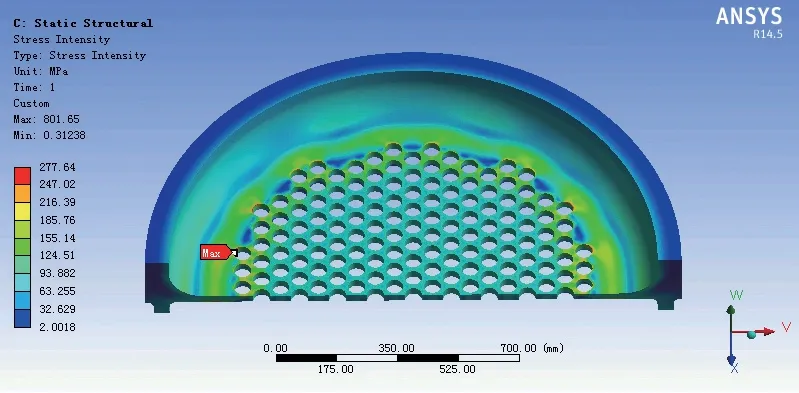
图21 模型C4 应力强度云图Fig.21 Stress intensity contour of model C4
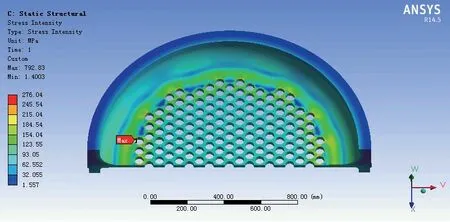
图22 模型C5 应力强度云图Fig.22 Stress intensity contour of model C5
由应力强度云图可知,翻边结构的厚度或者位置变化时,管板上的应力分布情况几乎不受影响,但翻边位置的变化会导致管板的应力强度最大点位置发生变化。同样的,在管板的低应力区取三条应力线性化路径S-1 ~ S-3,其结果列于表3 中。
表3 中,由模型C ~ C2、模型C3 ~ C5 的应力结果对比可知,当管板翻边的外径或者内径保持不变时,翻边厚度由30 mm 依次增加到45 mm、60 mm,管板的一次应力随着翻边厚度的增加而降低;由模型C 与模型C3、模型C1 与模型C4、模型C2 与模型C5 的应力结果两两对比可知,当管板翻边厚度相同时,翻边内径较小时,管板的一次应力也较低。通过上述分析对比可以发现,翻边结构相当于管板的一个加强环,加强环的厚度越大,刚度也越大,对管板的加强作用也就越强,并且厚度相同的加强环内径较小时其加强作用更好。
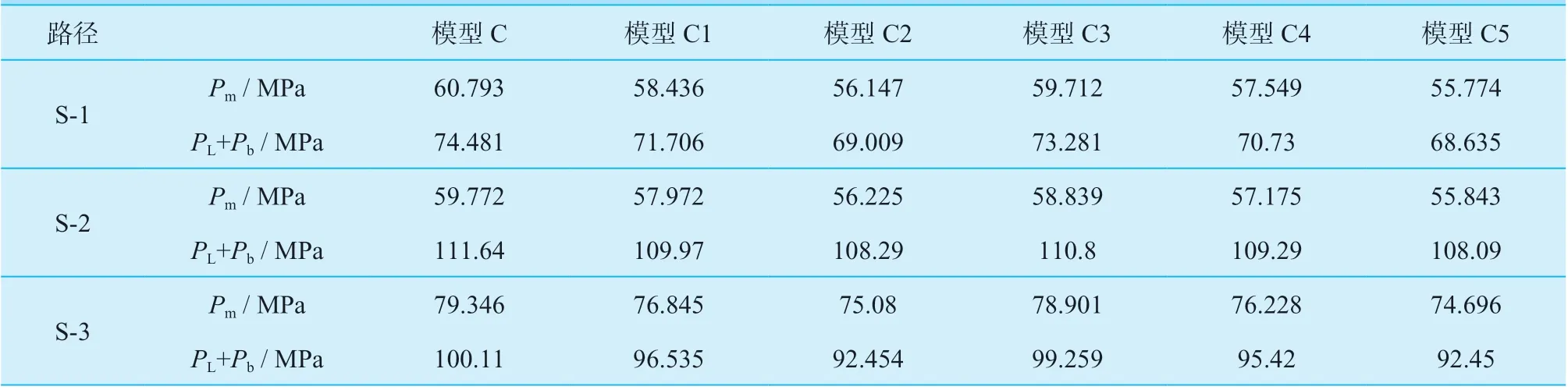
表3 模型C ~ 模型C5 的应力线性化结果Table 3 Stress linearization results of model C to model C5
5 结论
(1)本文采用有限元分析设计方法,通过建立不同管箱结构的挠性管板有限元模型,计算了各个模型的一次应力,对比分析了管箱结构对挠性管板一次应力的影响规律,对挠性管板结构的进一步优化和推广应用有一定指导性意义。
(2)挠性管板的法兰环(模型B)和翻边结构(模型C)均能降低管板的一次应力,对管板起到加强作用,且法兰环加强效果稍好,笔者认为带有法兰环的挠性管板(模型B)受力较复杂,推荐受力简单、综合性能更均衡的翻边结构(模型C)。
(3)以模型C 为基础,调整翻边结构的厚度和内径以作对比,经分析后得知:翻边结构外径或内径保持不变时,增加翻边厚度能降低管板的一次应力;翻边厚度保持不变时,减小翻边内径能降低管板的一次应力。

