基于分层人工鱼群的相干极化-DOA联合估计
曹丙霞,刘 威,李 享,闫锋刚,金 铭
(哈尔滨工业大学(威海)信息科学与工程学院 威海 264209)
引言
近年来,极化敏感阵列广泛应用于无源定位、雷达目标检测、天文观测等领域。相较于传统的标量传感器阵列,极化敏感阵列在获取入射电磁信号空间时延信息的同时还能完整地获得极化信息,以进一步提高系统测向性能[1]。在极化敏感阵列下进行信号估计时,若信号源中存在相干信号,传统基于非相干信号的估计方法性能会大幅下降。因此,相干辐射源下的极化-DOA 联合估计成为当前信号处理领域中亟须解决的热点问题。
标量阵列中求解相干信号的空间平滑(Spatial Smoothing,SS)算法可拓展到极化敏感阵列[2,3],算法通过划分相同阵型的子阵,然后求各子阵协方差矩阵的均值来恢复阵列协方差矩阵的秩。但该算法需要阵列存在多个空间平移不变匹配子阵才能实现,且平滑过程会损失部分阵列空间孔径。极化平滑(Polarization Smoothing,PS)算法[4−6]将相同极化方式的电/磁极子作为一组子阵,对阵型空间结构没有特殊要求,但会破坏信号的矢量结构,平滑后无法估计极化参数。子空间拟合算法[7,8]能在不损失阵列孔径和极化信息的同时,应用于相干信号,并适用于任意不存在流型模糊的阵型,但该方法需要多维搜索,计算复杂度较高。广义子空间拟合算法[9]在子空间拟合算法的基础上进一步利用信号极化导向矢量和空间相位矩阵存在的线性关系,实现空间参数和极化参数解耦的目的,降低了部分复杂度,但该方法在信号个数较多时仍需要多维搜索,计算复杂度较高。因此,对多维搜索进行优化以降低计算复杂度成为问题的关键。
现有的多维优化算法主要分为两类:解析类算法和智能优化类算法。其中,解析类算法是通过对多维搜索进行降维来降低计算复杂度。笔者对几种经典的解析类优化算法进行了研究,对比分析了各算法的原理思想及特点,分析结果如表1所示。其中交替投影(Alternating Projection,AP)算法[10]基于交替优化和投影矩阵分解,在迭代的每一步只对一个参数进行优化,但在低信噪比情况下性能较差。多项式参数化(Method of Direction Estimation,MODE)算法[11]是一种基于多项式求根思想的加权子空间拟合算法,该算法可以在二维空间谱中,利用相互耦合的不同轴向的阵列流型对投影矩阵进行参数表示,将二维空间搜索降维成两个一维搜索,但该算法要求阵型必须为方阵。修正变量投影(Modified Variable Projection,MVP)算法[12,13]是高斯牛顿迭代法的一种改进,它是针对信号子空间算法提出的,同样适用于多维非线性最大化问题,但信号相关系数较高时算法性能会发生恶化。

表1 解析类算法原理及存在的问题Table 1 Analytical algorithms principles and existing problems
智能优化类算法则是通过对搜索过程进行优化来降低复杂度,相较于解析类算法,其适应性更强、对目标函数要求更低。智能算法种类丰富,如经典的遗传算法(Genetic Algorithm,GA)、粒子群(Particle Swarm Optimization,PSO)算 法[14],以及近年新提出的人工鱼群算法[15](Artificial Fish Swarms Algorithm,AFSA)、萤火虫算法(Firefly Algorithm,FA)、蝗虫优化算法(Grasshopper Optimization Algorithm,GOA)、麻雀搜索算法[16](Sparrow Search Algorithm,SSA)等。其中的遗传算法、粒子群算法、萤火虫算法、蝗虫优化算法普遍存在搜索过程中易陷入到局部最优解的问题,通过对算法中个体采用柯西变异、混沌映射[17,18]等方法能在一定程度上增强算法跳出局部解的能力,但有较大的随机性。而人工鱼群算法中拥挤度因子的设置能有效限制个体聚群的规模,避免粒子全部陷入局部点。另外,算法的觅食行为也能增加算法的随机性,但该算法收敛速度慢,寻优能力不足。
本文基于人工鱼群算法,针对其收敛速度慢、收敛精度低的缺点,提出改进的分层人工鱼群算法(Hierarchical Artificial Fish Swarms Algorithm,HAFSA)。本算法采取预先设定的层次结构,将人工鱼群中的粒子作为底层,种群中的非最优粒子独立地进化,最优粒子则构成顶层在小范围内进行粒子群搜索,将得到的最优粒子传递回底层作为引导加快收敛速度。底层粒子负责全局搜索,顶层粒子负责局部搜索,能较好地保持探索与开发能力间的平衡,避免后期搜索盲目性较大的缺点。
1 数据模型及相关算法
1.1 数据模型
考虑N个波长为λ的远场窄带信号入射到阵元数为M的任意阵列上,信号快拍数为L,阵元采用正交偶极子天线,两通道对应相互垂直的x方向、y方向,可以输出两个垂直方向的电场信息。二维阵列的结构如图1所示。
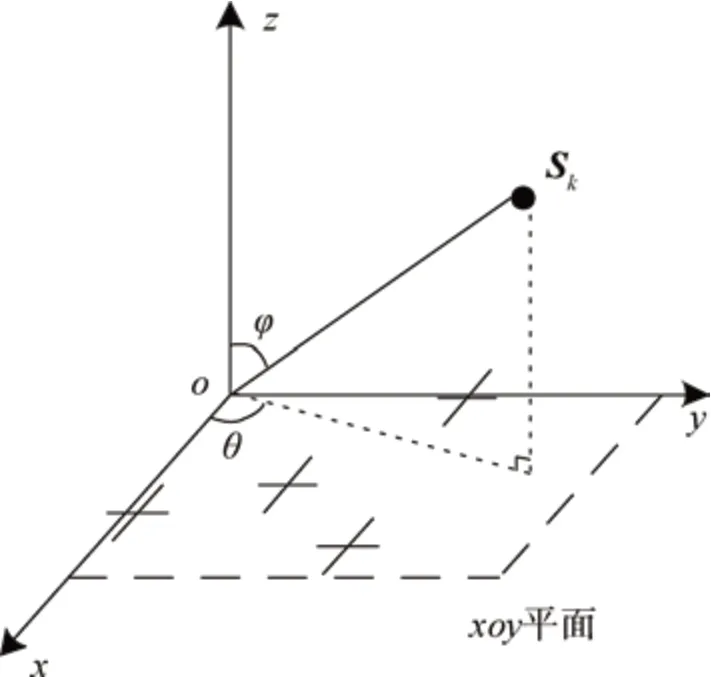
图1 二维阵列结构Fig.1 Structure of two-dimensional array
阵元接收数据为
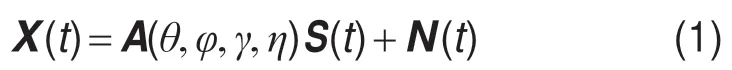
其中,X(t)是2M×L维快拍数据矢量,S(t)是N×L维信号矢量,N(t)是2M×L维高斯白噪声数据矢量,A(θ,φ,γ,η)是2M×N维导向矢量矩阵,且
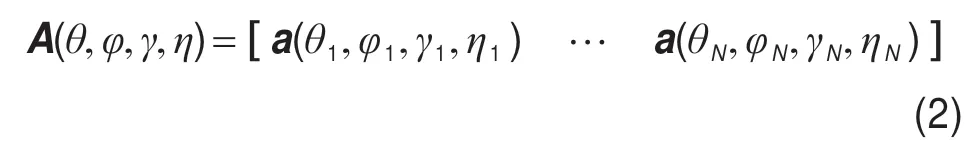
第n个信号的导向矢量a(θn,φn,γn,ηn)定义为:

其中"⊗"表示Kronecker积。
as为M×N维的空间导向矢量,第n个信号的空间导向矢量可表示为:
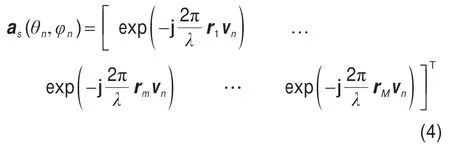
其中,rm为第m个阵元的位置,vn为第n个信号的方向矢量,可分别表示为
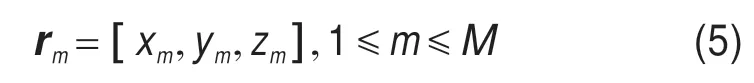
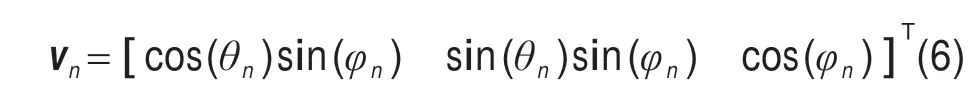
ap为2×N维的极化导向矢量,阵列第n个信号的极化导向矢量为:
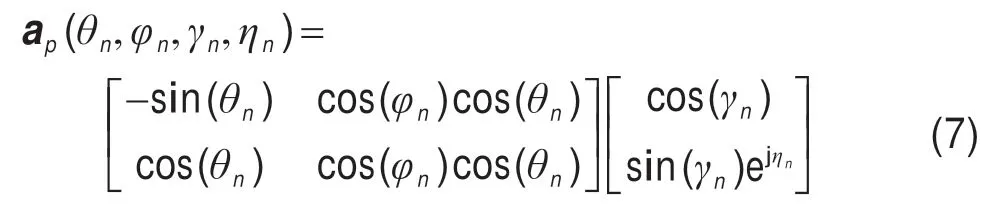
1.2 广义子空间拟合算法
将极化导向矢量ap构成的矩阵定义为:

信号模型进一步可表示为:
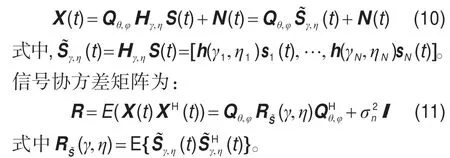
若N个信号中有N'个为相干信号,则的秩为(N-N'+1),即R特征分解后存在(N-N'+1)个大特征值。提取(N-N'+1)个大特征值对应特征向量,其张成的空间构成了协方差矩阵的信号子空间Us,而其余(2M-(N-N'+1))个小特征值对应的特征向量张成的空间对应了协方差矩阵的噪声子空间。信号子空间是阵列流型张成空间的一个线性子空间,即信号子空间和阵列流型之间存在线性关系,此时必定存在一个满秩矩阵T1使得

有噪声存在时,信号子空间与阵列流型张成的空间不相等,可构造拟合函数式(13)。通过式(13)中的最小二乘问题,得到信号空间参数的估计值:

因此,式(13)中的估计值可退化为:

同理,可得极化参数估计值:

广义子空间拟合算法角度搜索的过程为遍历搜索,若θ,φ,γ,η轴划分的网格数分别为G1,G2,G3,G4,则算法计算复杂度可表示为O((G1G2)N+(G3G4)N),可以看出算法复杂度与信号个数和参数维度呈指数关系,计算复杂度较大,在工程中难以实现。而智能优化算法可在多维问题中基于概率选取,通过求解部分目标函数值确定问题最优解。将广义子空间拟合算法中,对空间参数和极化参数进行谱峰搜索的谱估计函数,即式(15)和式(16)分别作为智能优化算法中的目标函数,从而在确定的空间和极化角范围内进行快速搜索,显著降低角度搜索的次数,可降低计算复杂度。
2 基于分层人工鱼群算法的极化-DOA联合估计
2.1 人工鱼群算法
人工鱼群算法通过模拟鱼群的觅食行为实现寻优。算法主要利用鱼的聚群、追尾、觅食三大基本行为特征,采取自下而上的寻优模式,从构造个体的底层行为开始,通过鱼群中各个体的局部寻优,达到全局最优点在群体中凸显出来的目的。
假设需要进行K维搜索,人工鱼的数量为D,则第i个人工鱼的位置可表示为Xi={x1,x2,…,xK},1 ≤i≤D;当前位置的食物浓度通过目标函数值Y=f(X)来表示。在极化-DOA 联合估计中,人工鱼的位置对应了可行的空间或极化角度,当前位置的食物浓度对应了角度对应的谱估计函数值;两人工鱼之间的距离为dij=;θvisual表示视野范围,对应了角度搜索范围;δ表示拥挤度因子;ntrynumber表示人工鱼觅食最大试探次数,即当前位置下寻找更大谱峰的尝试次数;λstep表示每次可移动的最大步长。图2为人工鱼视野和移动步长示意图。当人工鱼视野范围内XV处食物浓度高于当前位置X时,人工鱼前进一步到达Xnext位置:
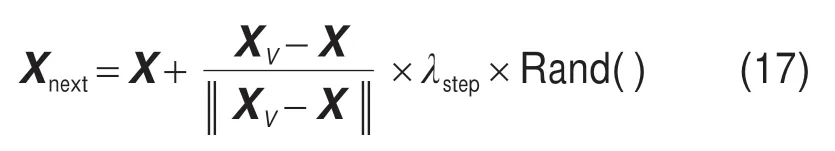
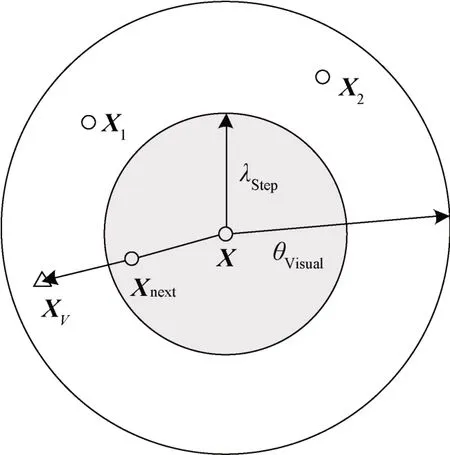
图2 人工鱼视野和移动步长示意图Fig.2 Schematic diagram of the field of view and moving step length of artificial fish
由于广义子空间拟合为组合优化类问题,对应的离散型鱼群算法模型原理如下。
2.1.1 觅食行为
人工鱼Xi在其视野θvisual内随机选取新位置Xj

在求极大值问题中(本文均以求极大值问题为背景),判断两位置的食物浓度,即两个角度下的谱峰高度,若Yj>Yi则证明新位置食物浓度更高,即谱峰值更大,人工鱼根据式(17)向Xj方向移动一步;否则重新选取Xj继续判断食物浓度,反复尝试ntrynumber次后,如果仍未找到满足的状态,则人工鱼随机前进。
2.1.2 聚群行为
探索人工鱼Xi视野范围内(即dij≤θvisual)鱼的数目nf及视野内鱼群的中心位置Xc,若Yc/nf>δYi,则说明中心位置食物浓度更高并且不太拥挤,即此处谱峰更高且区域内搜索谱峰的粒子数目较少,人工鱼根据式(17)向Xc方向移动一步。反之,算法执行觅食行为。

2.1.2 追尾行为
探索人工鱼Xi视野范围内(即dij≤θvisual)所处位置食物浓度最大的鱼的位置Xmax,若Yc/nf>δYi,则说明中心位置食物浓度更高且不太拥挤,人工鱼根据式(17)向Xmax方向移动一步;反之,算法执行觅食行为。

人工鱼群算法流程如图3所示。
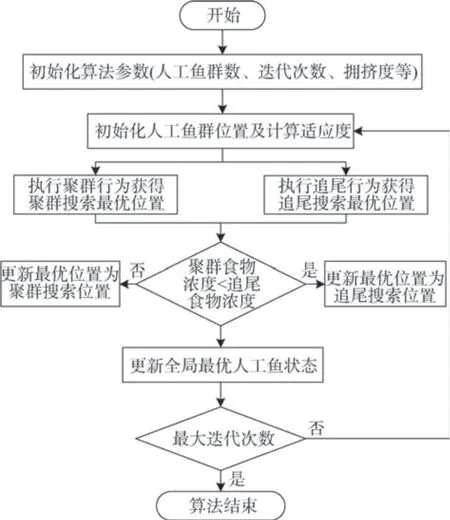
图3 人工鱼群算法流程图Fig.3 Artificial fish swarm algorithm flow chart
人工鱼群的三种基本行为特征以及拥挤度因子的作用使得其具有较好的鲁棒性,全局寻优能力强,且能及时跳出局部极值点。但算法的收敛速度慢,主要是由以下因素导致:
①在解决最优化问题时,鱼群的追尾行为起到非常重要的作用,人工鱼视野中的最优点将为鱼群的移动方向提供引导。但传统人工鱼群算法中,当人工鱼个体距最优点较近时,仍采用随机寻找的方法较为盲目,若加大ntrynumber次数则会大大增加算法复杂度,导致收敛速度变慢。
②鱼群在执行觅食行为时,若没有发现食物浓度更高的位置则会进行随机选择。该方法能一定程度扩展搜索范围,但也会出现算法退化的情况(如鱼群中最优点进行随机选择大概率会获得更差的点),没有充分利用已经获得的先验有利信息。这种情况下,算法过于注重探索能力而削弱了开发能力,导致算法收敛速度变慢,甚至无法收敛。
仅是人工鱼群算法仍不能完全解决极化-DOA联合估计对空间和极化角快速搜索的要求,需要改进其收敛速度以适应工程需求,而粒子群算法结构简单,收敛速度快,适合解决该问题。
2.2 粒子群算法
粒子群算法通过设计一种无质量的粒子来模拟鸟群中的鸟,并赋予粒子速度和位置两个属性。速度代表粒子移动的方向和距离,位置代表粒子在多维空间中所处的状态。每个粒子在搜索空间中独立进行搜索,将搜索到的最优点作为个体极值,并将个体极值与群体中其他粒子进行分享,找到全部粒子中最优的个体作为全局极值点。粒子会根据自身最优极值点和群体中共享的全局最优解极值点来调节自身的速度,再由当前位置和速度确定粒子下一次的位置。由于粒子信息是单向流动的,粒子受已搜索到的最优点影响较大,适合局部最优点的搜索。粒子群算法流程如图4所示。
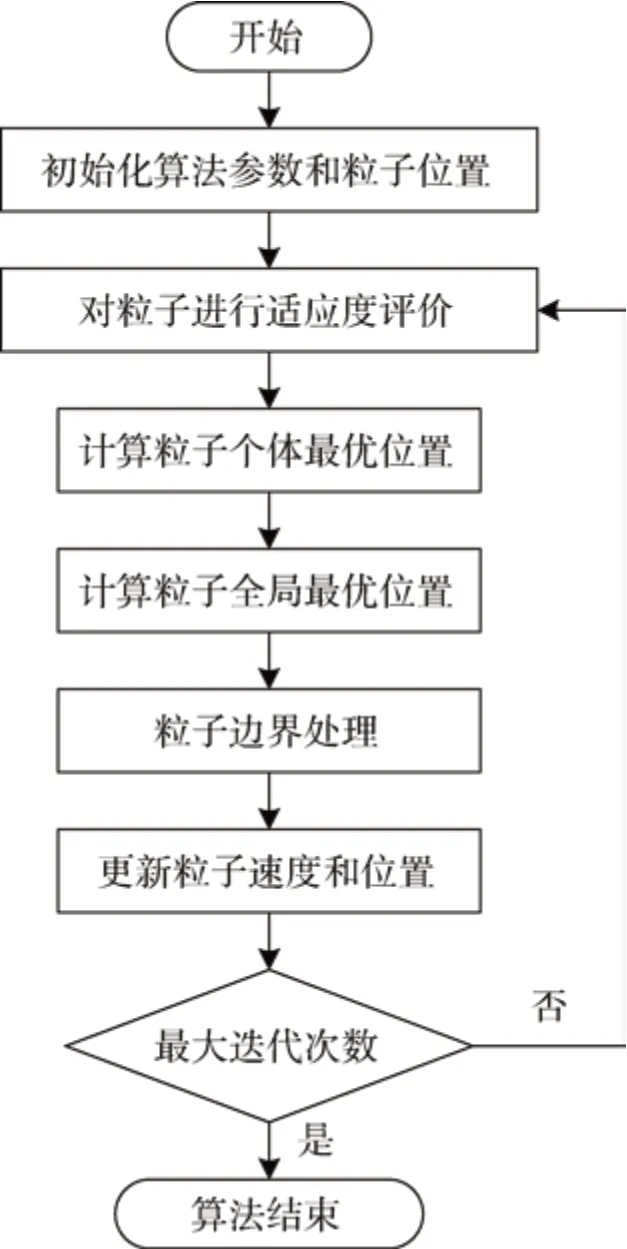
图4 粒子群算法流程图Fig.4 Particle swarm algorithm flow chart
极化-DOA 联合估计中,粒子的位置对应了可行的空间或极化角度,粒子的速度对应去往下一个位置的方向和距离,适应度值对应了当前角度对应的谱估计函数值即谱峰值。设有D个粒子L={L1,L2,…,LD}组成的群体对K维空间进行搜索。第i个粒子的位置为Li={l1,l2,…,lK},i=1,2,…,D,粒子对应的速度表示为Vi={vi1,vi2,…,viK},不同粒子之间通过适应度值来对比优劣。粒子在搜索时还需考虑两个因素:粒子本身搜索到的个体历史最优点Ti={ti1,ti2,…tiK}和全部粒子搜索到的最优值Tg={tg1,tg2,…tgK}。其中历史最优点Tg只有一个。
算法位置和速度更新公式为:
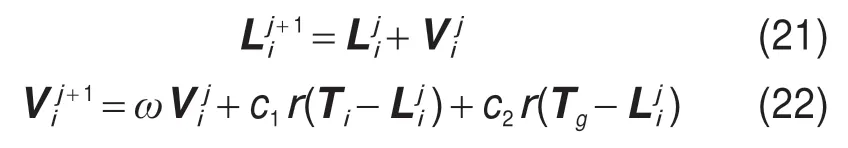
其中,j为搜索次数,ω为惯性因子,c1和c2分别为针对自身和群体的学习因子,r为0~1 之间均匀分布的随机变量。
2.3 分层人工鱼群算法
人工鱼群算法为解决最优化问题提出,并在路径规划、资源调度、聚类问题等一系列优化问题方面取得了较好的效果,但存在收敛速度慢的问题。在解决广义子空间拟合多维搜索复杂度高的问题上,为实现信号波达方向估计快速寻优,结合粒子群算法收敛速度快、适合局部寻优的特点,本文基于以下思想,对智能寻优算法进行改进:
①将算法分为底层和顶层。底层采用人工鱼群算法,负责主要的全局搜索;顶层采用粒子群算法,负责局部搜索。人工鱼群算法迭代一定次数后,将鱼群中现有的最优点传递到顶层;顶层利用粒子群算法收敛速度快的优点,在现有最优点附近小范围寻找极值点,小范围搜索可保证粒子群不易收敛到局部极值点;之后,将搜索到的极值点传回底层。通过分层来快速寻找极值点,加速算法收敛效率。二维搜索情况下分层人工鱼群算法结构示意图如图5所示。
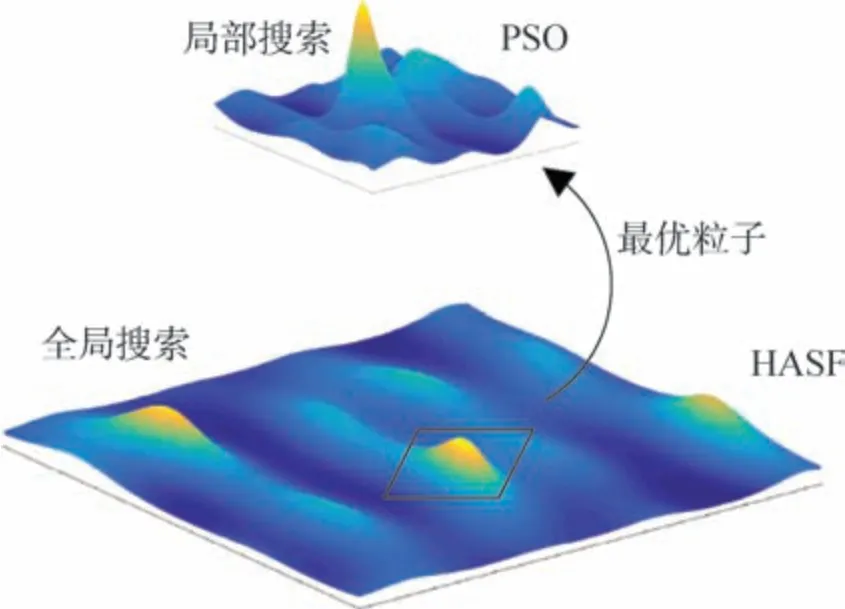
图5 分层人工鱼群算法结构示意图Fig.5 Structure diagram of HAFSA
②每次迭代后,若鱼群中最优个体没有改善,则保持其不变,除最优个体外的其余个体可以通过随机选择行为更新位置状态。这样可以在较好地保留有利信息的同时,继续探索新的空间,有利于保持两者间的平衡,避免出现最优个体进行随机的觅食行为反而导致算法退化的情况。
表2 给出了极化-DOA 联合估计与分层人工鱼群算法关键参数的映射关系。

表2 极化-DOA联合估计与分层人工鱼群算法关键参数映射关系Table 2 The mapping relationship between HAFSA and Polarized DOA joint estimation problem
用于相干极化-DOA 联合估计的分层人工鱼群算法具体步骤如下。
步骤1:构造阵列接收信号X(t)通过式(11)获得数据协方差矩阵,特征值分解后得到信号子空间。
步骤2:确定信号搜索范围和搜索步长,通过编码完成角度到个体鱼或粒子的映射。
步骤3:公式(15)是估计信号空间参数的适应度函数,先初始化人工鱼群算法参数,并进行全局搜索,迭代一定次数后将其中的最优粒子传递给顶层,在顶层中初始化粒子群算法参数,在该粒子附近进行小范围搜索,获得极值点,传回底层人工鱼群算法,达到收敛条件后停止迭代。
步骤4:估计信号的极化参数,采用式(16)作为适应度函数,其余流程与步骤2相同。
步骤5:对得到的搜索结果解码,获得估计的角度参数。
整体算法和分层人工鱼群算法对应流程图如图6所示。

图6 整体算法和分层人工鱼群算法流程图Fig.6 Overall algorithm and HAFSA flow chart
3 仿真实验
为证明本文算法的可实施性和有效性,将本文提出的分层人工鱼群算法与其他智能算法进行计算机仿真实验对比,对比算法包括传统人工鱼群算法、自适应视野人工鱼群算法、麻雀算法和蝗虫优化算法。
3.1 仿真实验1——算法有效性分析
阵型采用8 阵元均匀圆阵,圆阵半径为λ,阵元为共点式正交的双偶极子天线。相干信号源数目设置为2 个,信号频率为6 GHz,快拍数为200,
图7 给出100 次蒙特卡洛仿真的空间参数和极信噪比为20 dB,信号相对复增益为1、e-j(π/6)。入射的空间角分别为(θ1,φ1=1°,2°),(θ2,φ2=7°,8°),极化角为(γ1,η1=15°,15°)和(γ2,η2=32°,25°)。各算法的空间角搜索范围为(-30°,30°),极化角搜索范围为(-10°,50°),搜索间隔为0.17°。
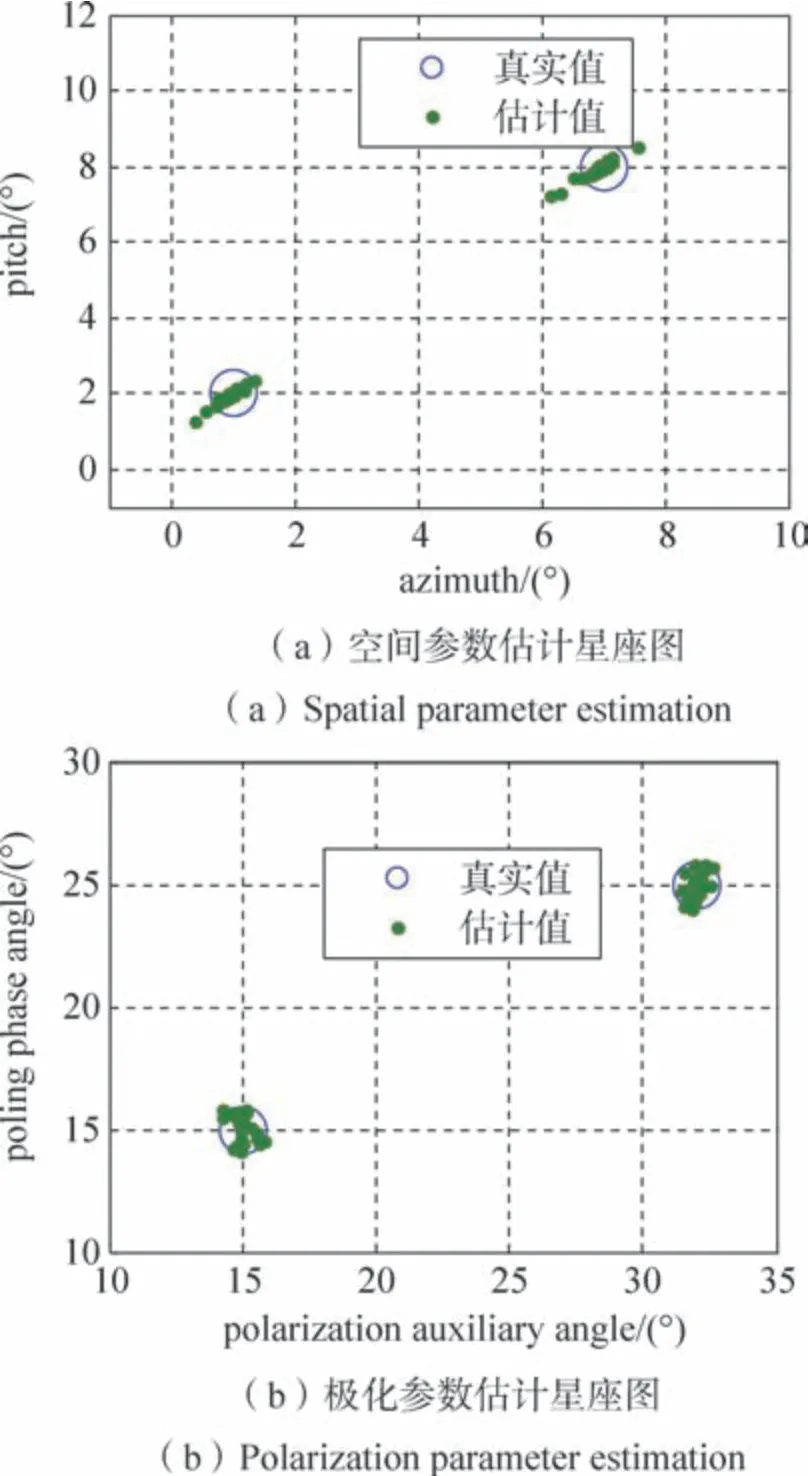
图7 信号估计星座图Fig.7 Signal estimation constellation
分层人工鱼群算法中底层空间角搜索范围为(-30°,30°),极化角搜索范围为(-10°,50°)。底层搜索后将搜索到的最优点传递给算法顶层,之后顶层在最优点5°范围内进行粒子群搜索。之后将新得到的最优点传递回底层,如此迭代直到算法满足收敛条件。算法参数设置如表3、表4所示。化参数的估计星座图,从图中可以看出分层人工鱼群算法能正确估计出目标方位角、俯仰角、极化辅助角、极化相位差四维参量且角度匹配正确。

表3 底层搜索算法参数设置Table 3 Low-level search algorithm parameter settings

表4 顶层搜索算法参数设置Table 4 Top-level search algorithm parameter settings
3.2 仿真实验2——算法精度分析
设置范围为0~30 dB、间隔为5 dB 的信噪比区间,每个信噪比下进行独立500 次蒙特卡洛实验。其余仿真条件与仿真实验1 相同。定义均方根误差为:
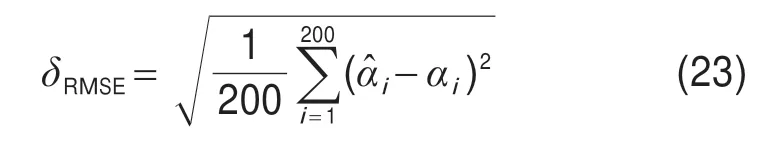
考察AP和MVP两种解析算法在不同信噪比下的测角性能如图8(a)和图8(b)所示,可以看出两种算法的参数估计均方根在此时条件下,性能均不理想。智能算法中迭代次数和种群规模越大,算法复杂度越高。为保证仿真实验中算法对比的合理性,将三种人工鱼群及其改进算法(AFSA、AVAFSA、HAFSA)中的各项参数设置为相同数值,并将五种算法种群规模统一设置为30,迭代次数不固定。
为实现固定时间对比各算法精度,此处通过调整算法的迭代次数将算法运行时间调整到3秒附近,入射信号1中各参数估计均方根误差曲线如图8(c)~图8(f)所示。根据仿真图可以看出:随着信噪比的增加,各算法空间和极化估计参数的均方根误差都会减小;根据图8(c)~图8(f)可以看出:相同信噪比下极化角均方根误差大于空间角均方根误差;当信噪比小于10 dB 时,五种算法各角度均方根误差相近,信噪比大于10 dB时,HAFSA算法测角精度与GOA算法相近,两者测角精度优于其他算法。

图8 算法角度均方根误差曲线图Fig.8 Algorithms angle RMSE curve
广义子空间拟合求解角度为多维非线性最优化问题,多个维度同时进行求解,单个角度均方根误差曲线图无法体现出整体估计情况,目标函数值可反映所有信号空间或极化角的估计情况。为更精确体现出算法的精度,图9给出了仿真实验2 条件下各算法目标函数值随信噪比变化曲线图。从图中可以看出,相同信噪比下分层人工鱼群算法搜索到的目标函数值最大,可以体现出分层人工鱼群算法在各信号参数的综合估计精度优于其他四种算法。
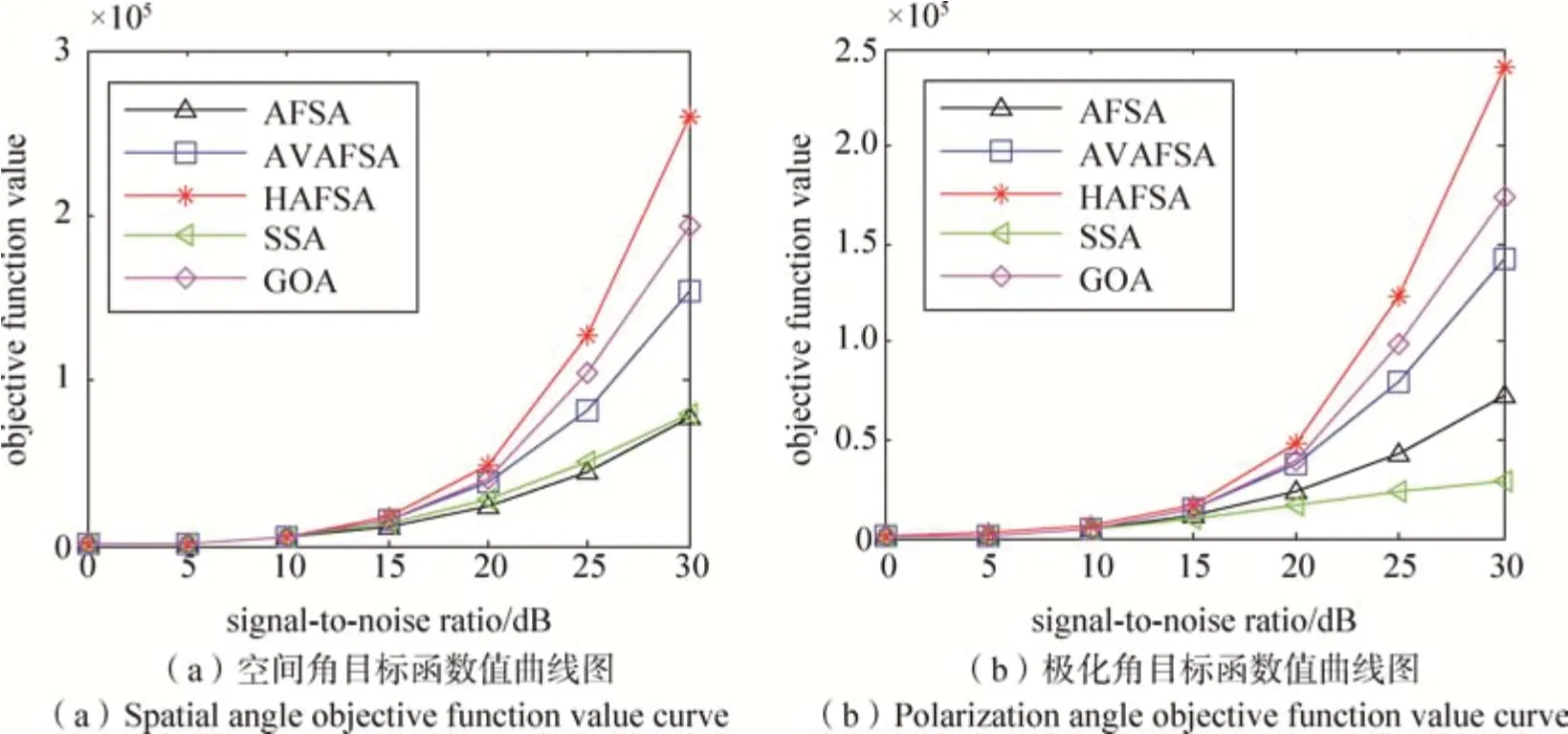
图9 算法角度目标函数值图Fig.9 Algorithms objective function value curve
3.3 仿真实验3——算法收敛性分析
由于智能优化算法内有大量的随机因素,算法收敛情况会在一定范围内波动。为更清晰地体现各算法收敛性,此处同样设置信噪比范围为0 dB~30 dB,每间隔5 dB 进行200 次独立的蒙特卡洛实验,若算法在6秒内估计出的信号空间角与原始信号空间角度误差绝对值小于0.5°,极化角和原始极化角度误差绝对值小于1°,则判定算法收敛成功,记录算法运行时间;反之,则判定算法无法收敛。其余仿真条件与仿真实验1相同。
图10 给出各算法收敛成功概率及收敛时间。由图可以看出信噪比较低时,各算法收敛概率和收敛时间接近。当信噪比变大,相同信噪比下,GOA 算法收敛概率高,但收敛所需时间长,HAFSA 算法收敛概率最高,收敛所需时间最短。基于概率搜索的智能优化算法可通过优化搜索过程来降低计算复杂度,其复杂度没有具体的解析表达,本文仿真以收敛时间来说明不同智能算法的计算复杂度,图10 可以证明:HAFSA 算法能大幅降低广义子空间拟合算法的计算复杂度。
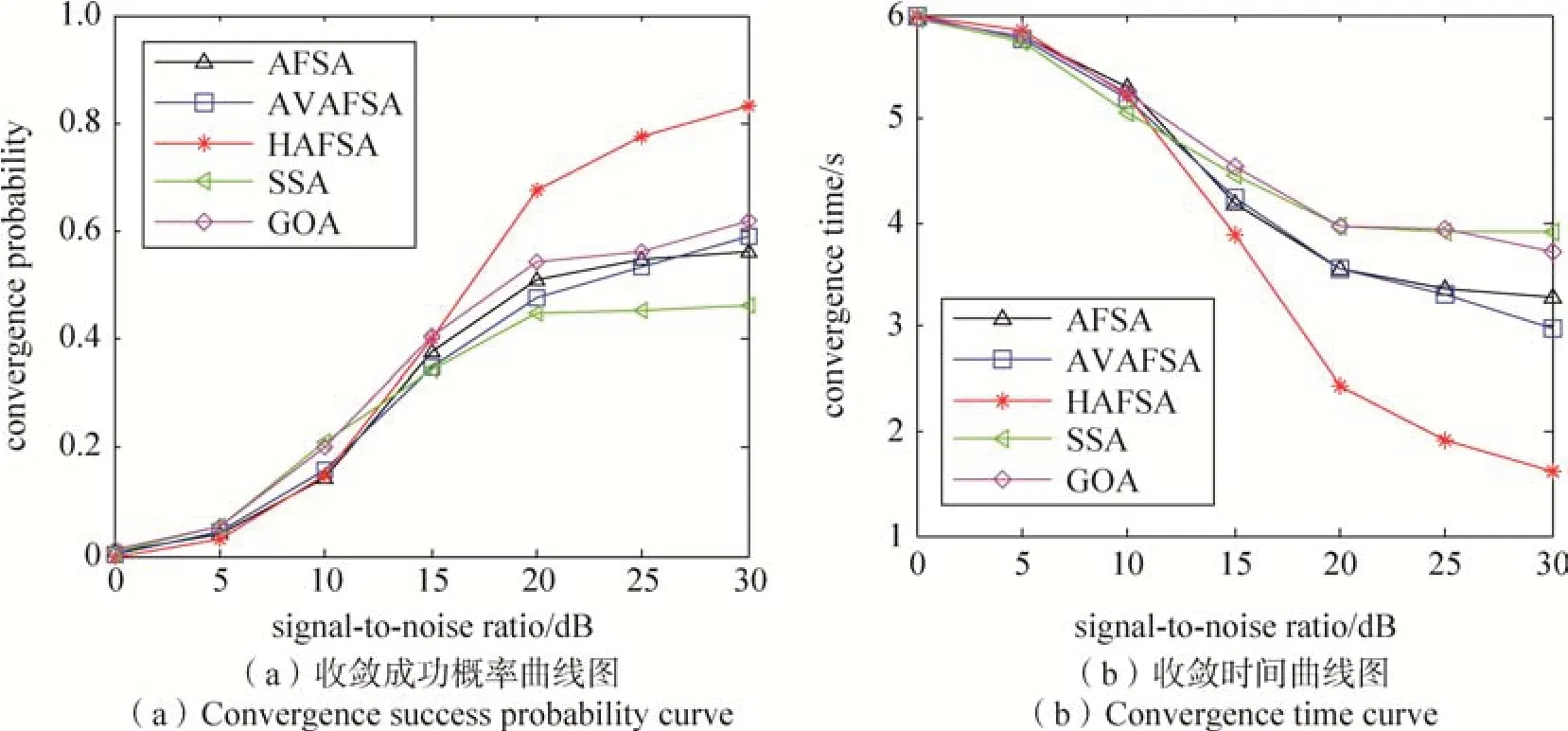
图10 三种算法收敛概率和收敛时间曲线图Fig.10 Convergence probability and convergence time curves of three algorithms
4 结束语
本文基于降低广义子空间拟合算法多维搜索复杂度的思想,提出一种融合粒子群的分层人工鱼群算法。针对人工鱼群算法收敛速度慢的问题,构造顶层结构并使用结构简单的粒子群算法在局部范围快速搜索最优点,优化了搜索过程,减少了计算次数,有效降低了计算复杂度。仿真实验表明:分层人工鱼群算法测角性能优于常见的智能优化算法,并且该算法在收敛速度方面有较大的提升,更能适应实时计算的环境要求。

