长江上游径流对气象要素变化的敏感性分析
沈嘉聚,杨汉波,刘志武,杨大文
(1.中国长江三峡集团有限公司科学技术研究院,北京 100038; 2.清华大学水利水电工程系,北京 100084;3.清华大学水沙科学与水利水电工程国家重点实验室,北京 100084)
由于气候变化、社会经济发展以及长江上游水资源开发利用的影响,近年来长江上游径流发生了较大变化[1-5]。开展长江上游径流对气候变化的响应研究可以为长江上游水电开发、梯级水库优化调度运行提供依据,对流域水资源规划、开发利用与保护具有重要意义。目前,径流变化的分析方法可归纳为3类:水文模型情景模拟法[6-10]、统计模型相关分析方法[11-14]和基于Budyko框架的弹性系数法[15-17]。水文模型情景模拟法采用的模型通常具有良好的物理基础,但模型结构与模型参数存在一定的不确定性,且对输入数据要求较高[18-20];统计模型运算简单,但自变量之间的相关性往往会影响归因结果;基于Budyko框架的弹性系数法,因其物理意义清楚、所需资料易于获得而被广泛应用,但长时间序列中的噪声通常会对归因结果产生影响[21-22],因此在归因分析时通常采用多种分析方法进行对比验证[7]。根据水文模型情景模拟法中采用模型的建模原理可以分为过程驱动模型和数据驱动模型,过程驱动模型在不同区域参数需要分别率定,可能产生较大不确定性,且应用较为复杂;随着数据科学与高性能计算的快速发展,基于机器学习方法的数据驱动模型能快速从大量数据中训练学习得到有效信息,并用于未来变化情景的预测,因而受到广泛关注[23]。BP神经网络是机器学习中较为成熟的一种算法,通过反向传播算法训练由输入层、输出层及若干隐藏层的节点相互连接而成的多层前馈网络,具有很强的非线性映射能力,但其初始权值与阈值为随机选取,容易在网络训练过程中陷入局部最小值[24];而遗传算法则是模仿生物演替过程中的选择、交叉、变异和优胜劣汰的筛选过程,具有很好的全局搜索性,能够为神经网络中不确定的初始权值与阈值寻找全局最优解[25],从而提高模型准确性。
在全球变暖的大背景下,气候变化对长江上游径流产生了重要影响[26]。以往对于长江上游气象要素对径流影响的研究主要通过统计方法[13-14,26-27]进行定性分析,以及利用传统水文模型情景模拟法[7-8,10]进行定量归因,而运用机器学习算法通过情景模拟进行敏感性分析的研究较少。因此,本文运用遗传算法优化的BP神经网络(genetic algorithm optimize BP neural network,GA-BP)算法替代传统水文模型,分析长江上游径流对降水与气温变化的敏感性,并与多元线性回归法及基于Budyko框架法的结果进行对比,探究近年来长江上游年径流量变化趋势及其气象驱动因子。
1 研究区概况与研究数据
1.1 研究区概况
长江上游是指宜昌水文站控制的流域,包括金沙江、岷江、乌江、嘉陵江等水系的流域区域(图1),流域面积约100万km2。长江上游区域地形复杂,包括青藏高原、四川盆地,涉及青海、云南、甘肃、四川、贵州等多个省份,气候受青藏高原、东南季风以及西南季风的综合影响,区域内空间差异较大。长江上游年均气温10~15℃,呈自西向东递增的分布规律;年平均降水量800~1 200 mm,呈自西北向东南递增的分布规律。除源区、高山区域多降雪,长江上游径流以降水补给为主,径流主要集中在夏季,雨热同期,洪水具有洪峰高、洪量大、持续时间长等特点。
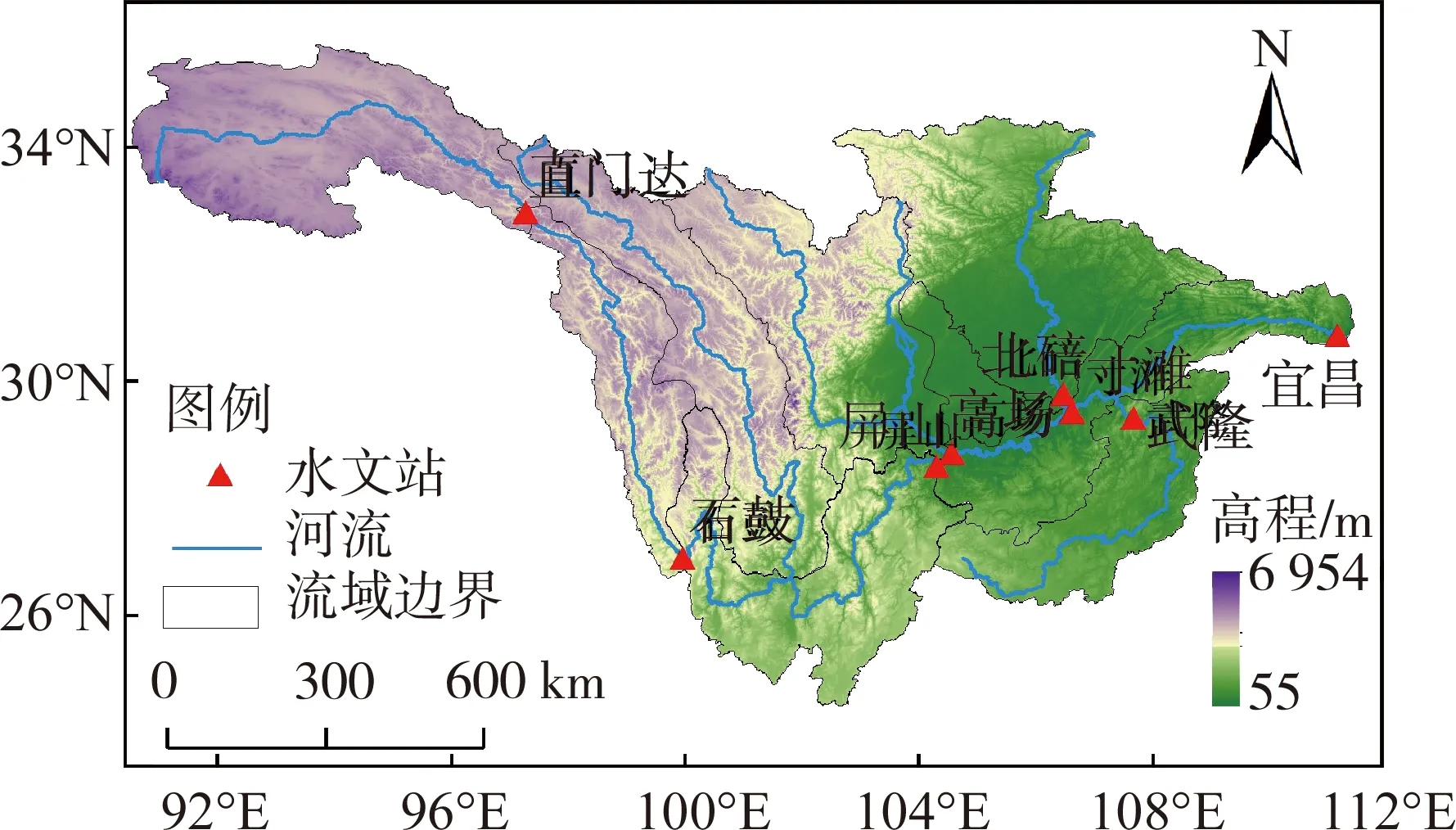
图1 研究区域及水文站点分布Fig.1 Study area and distribution of hydrological stations
1.2 研究数据
收集了长江上游8个水文站(直门达、石鼓、屏山、高场、北碚、武隆、寸滩和宜昌)1979—2015年逐日径流数据。同时期的气象数据来源于国家青藏高原科学数据中心(National Tibetan Plateau Third Pole Environment Data Center, TPDC)的中国区域地面气象要素驱动数据集(China Meteorological Forcing Dataset, CMFD)[28-29],包括近地面气温、地面向下短波辐射与降水强度,时间分辨率为1 d,水平空间分辨率为0.1°。潜在蒸散发量ET0采用国际粮农组织(FAO)推荐的潜在蒸散发计算方法[30]简化参数推导得到的Irmak-Allen公式[31](式(1))进行估算,该公式在Penman-Monteith公式基础上根据美国湿润地区的数据进行线性简化得到[31],在长江流域有较好的适用性[32-33]。
ET0=-0.611+0.149RS+0.079T
(1)
式中:RS为太阳辐射量,MJ/m2;T为日平均气温,℃。
2 研究方法
2.1 GA-BP算法
GA-BP算法的具体流程如图2所示。神经网络输入变量为当日降水量、前6 d降水量和日平均气温,输出变量为日径流量,神经网络由输入层、隐藏层和输出层构成,各层神经元数量分别为8、16、1。与水文模型情景模拟法类似,前80%的数据为训练集,剩余20%数据为测试集。采用纳什效率系数(NSE)、相关系数(R2)和均方根误差(RMSE)评估GA-BP算法的模拟效果。计算径流对气象要素变化敏感性时,对测试集输入变量施加一微小变化量,考虑实际降水与气温的变化,取该气象要素的3%进行扰动,得到新的输出。敏感性系数为输出变量的变化量与输入变量的变化量的比值。
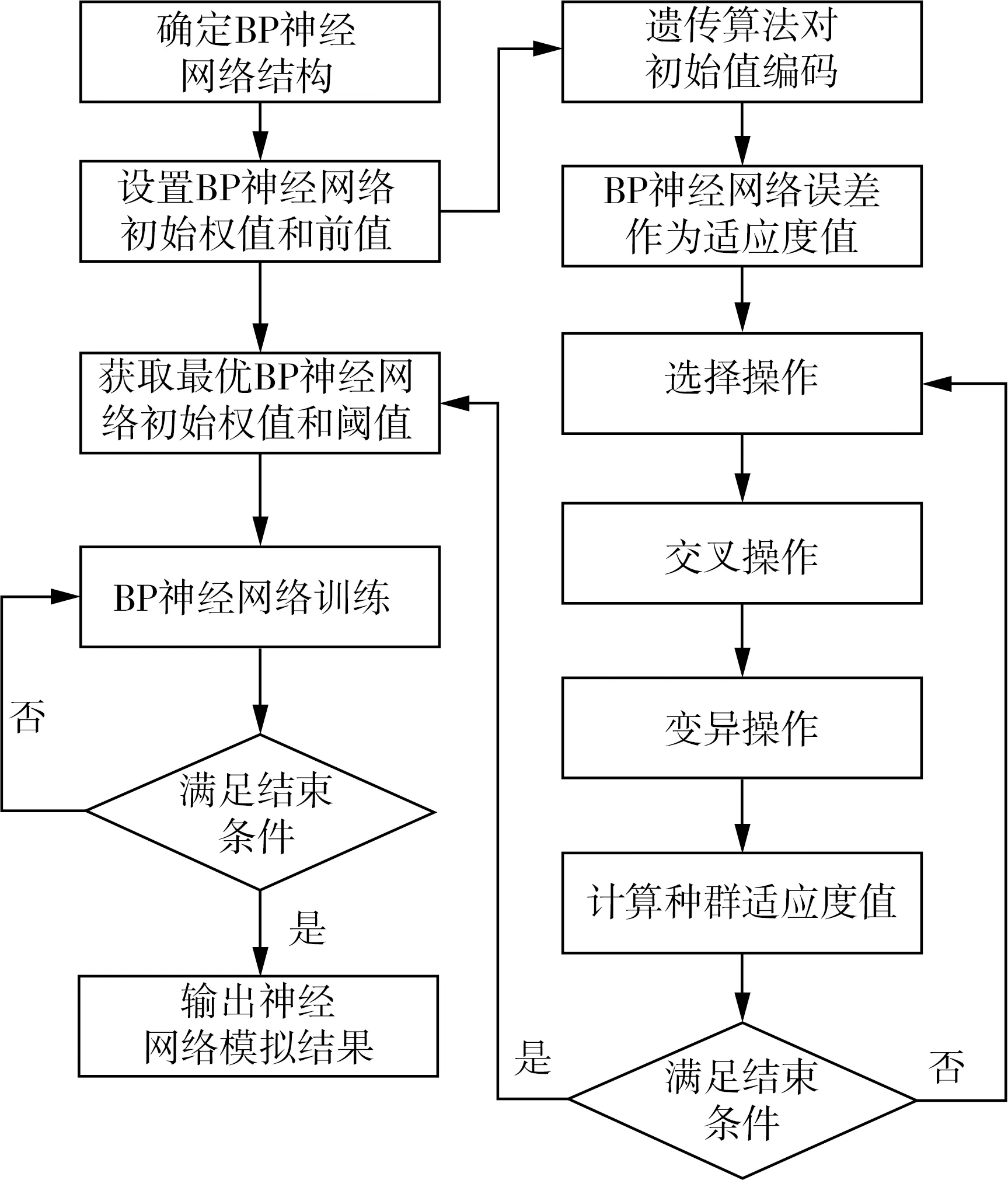
图2 GA-BP算法流程Fig.2 GA-BP algorithm flowchart
2.2 多元线性回归法
趋势分析采用多元线性回归法,显著性水平p取0.01,该方法通过多个自变量进行线性组合共同预估因变量。假设年径流R与年降水P、年气温Ty之间存在线性相关关系:
R=β0+βPP+βTTy+ε
(2)
式中:β0为回归常数;βP、βT分别为径流对降水和气温变化的敏感性系数;ε为回归残差。
2.3 Budyko框架法
Budyko框架法假设流域实际蒸散发量可以表示为流域降水量和潜在蒸散发量的函数[34],据此Choudhury等[35-36]提出了Choudhury-Yang公式:
(3)
式中:ET为实际蒸散发量,mm/a;n为下垫面参数,综合反映了地形、土壤、植被等因素影响。结合多年流域水量平衡方程:
R=P-ET
(4)
n可根据R、P、ET0的多年平均值反算求得,并假定在研究期间不变。将年径流量R的变化趋势表示为全微分形式:
(5)
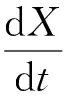
3 结果与分析
3.1 径流、降水及气温的变化趋势
表1为长江上游各水文站1979—2015年径流、降水量及气温的变化趋势。可见,径流增加趋势最大的为直门达站,达0.69 mm/a;减少趋势最大的为高场站,为2.81 mm/a。沿长江干流从上向下,径流变化由直门达站、石鼓站、屏山站的增加趋势,逐渐转变为高场站、北碚站、寸滩站、武隆站和宜昌站的下降趋势;值得注意的是,在p=0.01的显著性下,除高场站外其余站点变化趋势均不显著。降水量方面,直门达站和石鼓站控制流域显著增加(p<0.01),分别为4.28 mm/a和3.13 mm/a;屏山、寸滩和宜昌站点控制流域呈不显著增加,其余站点控制流域呈不显著减少。气温方面,各站点控制流域内气温均呈现显著上升趋势(p<0.01),变化范围从武隆站的0.021℃/a到直门达站的0.062℃/a。

表1 长江上游各水文站控制流域1979—2015年径流、降水及气温的变化趋势Table 1 Trends in runoff, precipitation and air temperature at hydrological stations in upper reaches of the Yangtze River from 1979 to 2015
3.2 GA-BP算法径流模拟
表2为GA-BP算法径流模拟结果。8个水文站训练集的NSE均值为0.71,R2均值为0.71,RMSE均值为0.59 mm/d;测试集NSE均值为0.61,R2均值为0.64,RMSE均值为0.55 mm/d,整体模拟效果良好。直门达站、石鼓站以及宜昌站模拟效果最好,训练集NSE值均高于0.7,测试集NSE值均高于0.6;北碚站和武隆站的模拟效果相对较差,主要是因为日径流数据波动较大,GA-BP算法对洪峰模拟效果较差,从而拉低整体模拟效果。
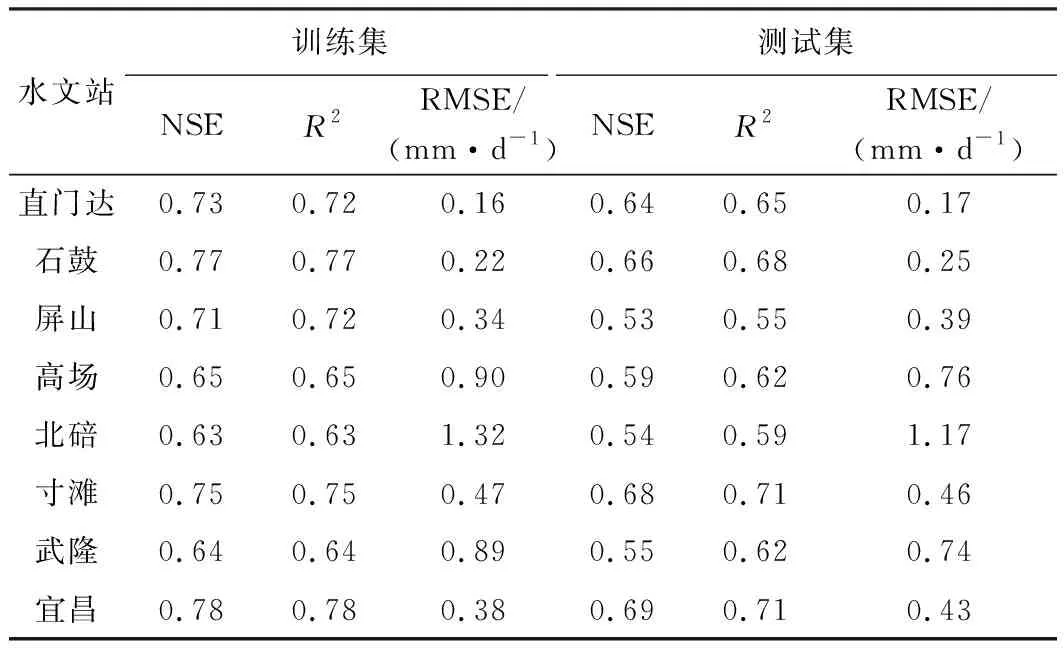
表2 GA-BP算法径流模拟结果Table 2 Results of GA-BP algorithm runoff simulation
3.3 径流对气象要素变化的敏感性
表3为3种方法得到的长江上游各水文站径流对降水、气温变化的敏感性系数。对于径流对降水的敏感性,多元线性回归法得到的各站点敏感性系数均值为0.65 mm/mm,GA-BP算法和Budyko框架法得到的结果分别为0.52 mm/mm和0.72 mm/mm;对于径流对气温的敏感性,多元线性回归法、GA-BP算法以及Budyko框架法的各站点敏感性系数均值分别为-20.94 mm/℃、-17.99 mm/℃和-18.96 mm/℃。3种方法计算径流对降水的敏感性均值最小的是直门达站,为0.37 mm/mm,最大的是高场站,为0.76 mm/mm;对气温的敏感性均值最小的时直门达站,为-4.77 mm/℃,最大的是高场站,为-33.53 mm/℃。沿长江干流从上向下,各水文站径流对降水的敏感性总体呈现增加趋势,即下游区域径流对降水的变化更为敏感,径流对气温的敏感性同样呈现增加趋势。

表3 长江上游各水文站径流对降水和气温的敏感性系数Table 3 Sensitivity coefficient of runoff of hydrological stations in upper reaches of the Yangtze River to precipitation and temperature
3.4 气象要素对径流变化的贡献量
表4为长江上游各水文站降水和气温对径流变化的贡献量,可见,多元线性回归法、GA-BP算法和Budyko框架法得到的降水导致径流变化的范围分别为-0.89~1.19 mm/a、-0.55~1.54 mm/a和-0.85~2.10 mm/a;气温导致径流变化的范围分别为-1.51~0.02 mm/a、-1.26~-0.01 mm/a和-1.11~-0.65 mm/a。与多元线性回归法相比,GA-BP算法得到的降水和气温变化导致径流的变化,在径流增加的石门达站和石鼓站结果偏大,在径流减少的高场站、北碚站、寸滩站、武隆站和宜昌站结果偏小。3种方法得到的降水对径流变化的贡献量均值的绝对值最小的是宜昌站,为0.15 mm/a,最大的是直门达站,为1.58 mm/a;气温对径流变化的贡献量均值的绝对值最小的直门达站,为-0.30 mm/a,最大的时北碚站,为-1.17 mm/a。沿长江干流从上到下各水文站降水对径流变化的贡献量整体上呈现减少趋势,气温对径流变化的贡献量呈现增加趋势。对于降水和气温对径流变化的贡献量,定义绝对值大者为主导因素。可以发现,直门达站、石鼓站、屏山站降水对径流变化的贡献量大于气温对径流变化的贡献量,而高场站、北碚站、寸滩站、武隆站以及宜昌站气温对径流变化的贡献量逐渐超过降水的贡献量,成为径流变化趋势的主导因素。

表4 长江上游各水文站降水和气温对径流变化的贡献量Table 4 Contribution of precipitation and temperature at hydrologic stations in upper reaches of the Yangtze River to runoff change
4 讨 论
4.1 GA-BP算法的敏感性
采用GA-BP算法进行径流对气象要素变化的敏感性分析时,输入变量的微小扰动都会影响敏感性系数的计算结果。为探究GA-BP算法计算径流对气象要素变化的敏感性结果的稳定性,降水扰动分别取测试集降水量均值的1%、2%、3%、5%和10%,气温扰动分别取测试集气温均值的1%、2%、3%、5%和10%,计算不同扰动得到的径流对气象要素变化的敏感性,结果见表5。可以看出,随着扰动程度的增加,GA-BP算法得到的径流对降水与气温的敏感性系数逐渐变小,且变化幅度同样变小并趋于稳定。考虑到采用较小扰动时计算误差对于敏感性结果影响较大,并且气象要素在1979—2015年的实际变化程度平均约3%,而且扰动在3%时其机器学习敏感性结果的波动幅度较小且趋于稳定,因此在利用GA-BP算法计算敏感性时,选择3%的扰动进行分析。

表5 不同程度扰动GA-BP算法敏感性计算结果Table 5 Sensitivity calculation results of GA-BP algorithm with different disturbances
为研究GA-BP算法利用不同时间尺度数据进行敏感性分析的适用性,分别采用日尺度和月尺度数据进行计算,结果见表6。可见,日尺度与月尺度计算结果中个别站点有所差异,但总体相差不大,计算结果稳定,所有站点的敏感性系数均值近乎相等。这意味着GA-BP算法不仅可以利用日尺度数据计算径流对降水与气温变化的敏感性,也可利用月尺度数据进行计算,从而可以在缺少日数据的流域进行应用。

表6 不同时间尺度数据GA-BP算法敏感性计算结果Table 6 Sensitivity calculation results of GA-BP algorithm using data of different time scales
4.2 长江上游径流敏感性与干旱指数的关系
沿长江干流从上向下,各水文站径流对降水与气温的敏感性总体呈增加趋势,高场站径流对气温的敏感性偏高,以下进一步探究这种分布形成的原因。直门达站、石鼓站、屏山站、高场站、北碚站、寸滩站、武隆站、宜昌站的干旱指数(ET0/P)分别为1.75、1.60、1.28、0.82、0.92、1.08、0.73和1.00,可见,高场站控制的流域干旱指数明显低于除武隆外的其他流域。图3为长江上游各水文站径流敏感性与干旱指数的关系。如图3(a)所示,径流对降水的敏感性与干旱指数间存在很强的线性关系,敏感性系数随着干旱指数的增大而减小;如图3(b)所示,径流对气温的敏感性随着干旱指数的增大而减小。对于气象要素的贡献量,如图3(c)所示,降水对径流变化的贡献量与干旱指数之间也存在显著的线性关系,敏感性系数随着干旱指数的增大而增大;如图3(d)所示,气温对径流变化的贡献量随着干旱指数的增大而减小。即降水对径流变化的影响在越干旱的区域影响越大,而气温对径流变化的影响在越湿润的区域越大,这与之前研究结果一致[37]。

(a) 径流对降水的敏感性

(b) 径流对气温的敏感性

(c) 降水对径流变化贡献量
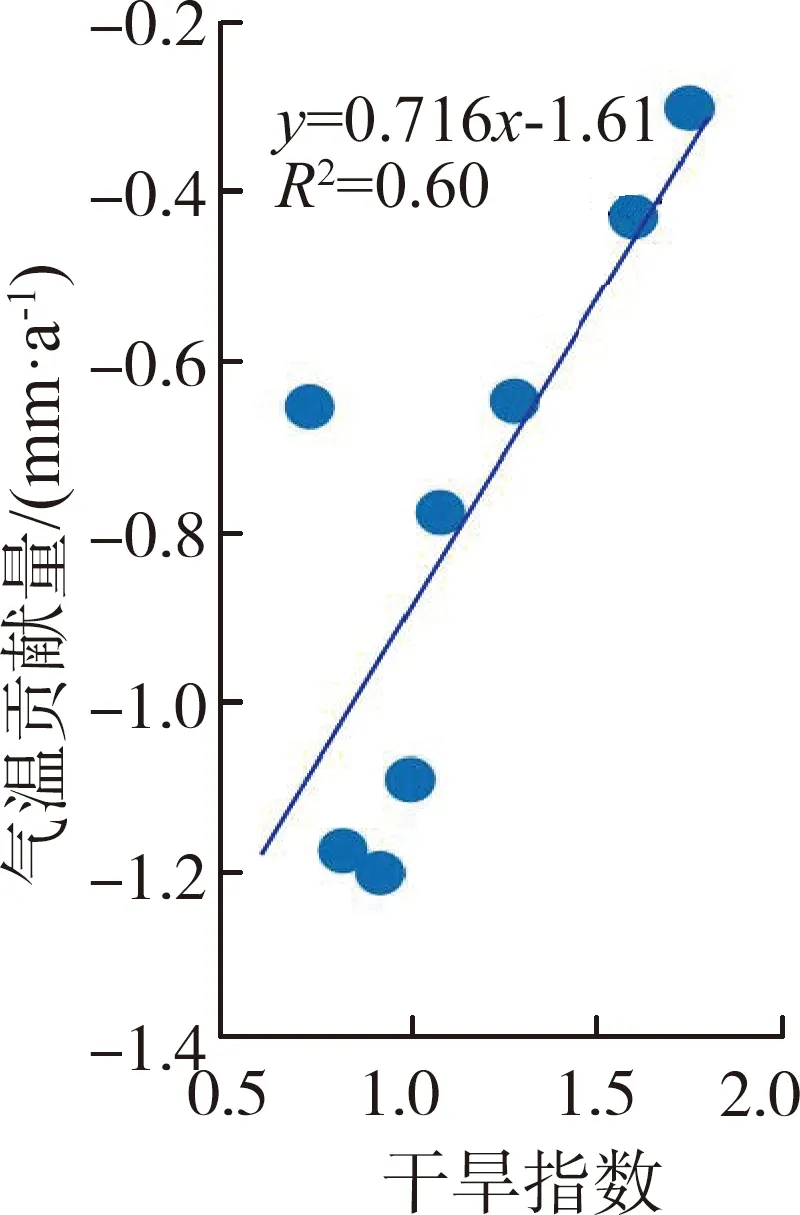
(d) 气温对径流变化贡献量图3 长江上游各水文站径流敏感性与干旱指数的关系Fig.3 Relationship between runoff sensitivity of hydrologic stations and drought index in upper reaches of the Yangtze River
4.3 不确定性分析
GA-BP算法对径流过程模拟效果较好,但对洪峰的模拟效果较差,NSE指标表现一般。以往研究运用机器学习法对长江上游进行径流模拟时,NSE值一般为0.6~0.8,如熊一橙等[38]利用LSTM算法模拟北碚站、高场站径流的NSE值分别为0.77、0.62;Zhu等[39]利用ANN算法模拟北碚站、高场站日径流NSE值为0.78、0.74;黄钰瀚[40]利用VIC模型对寸滩站日径流进行模拟,NSE值为0.80。对比以往研究,本文GA-BP算法对长江上游日径流模拟的结果相差不大。除此之外,在计算年径流量对年降水量与年均气温的敏感性系数时,日径流或洪峰的模拟效果不佳对于年径流量的计算结果影响不大,因此可以认为该方法尽管存在一定的不确定性,但得出的长江上游流域径流变化的敏感性总体是可信的。

本文计算得到的降水与气温对径流变化的贡献量,与实测值之间存在一定差异。导致这一差异的可能原因是只考虑了降水与气温对径流变化的影响,对其他气象要素、下垫面植被的变化以及人类活动的影响并未加以考虑。从结果来看,径流增加的直门达站和石鼓站,实测的增加值小于估计值;径流减少的高场站、北碚站、寸滩站、武隆站和宜昌站,实测的减少值大于估计值,可能原因是人类活动及植被变化导致耗水的增加、径流减少。
5 结 论
a.基于GA-BP算法的敏感性分析,利用日径流数据得到的结果整体较好,与多元线性回归法以及Budyko框架法的结果总体一致;对于缺少日径流数据的流域,该方法也可利用月数据进行计算。
b.年径流量方面,高场站显著减少(p<0.01),趋势为-2.81 mm/a,其余站点无显著变化;年降水量方面,直门达站和石鼓站显著增加(p<0.01),趋势分别为4.28 mm/a和3.13 mm/a,其余站点无显著变化;年气温方面,各站点均显著上升,幅度为0.021~0.062℃/a。
c.沿长江干流自上而下,径流变化对降水的敏感性系数由直门达站的0.37 mm/mm逐渐增大至宜昌站的0.74 mm/mm,最高为高场站的0.76 mm/mm;而径流变化对气温的敏感性也呈现增大趋势,范围从-4.77~-33.53 mm/℃;敏感性与干旱指数相关,随着干旱指数的增加,径流变化对降水和气温的敏感性减小。
d.从对径流变化的贡献量来看,降水的贡献量沿干流自上而下逐渐变小,气温的贡献量无明显规律。其中直门达站、石鼓站、屏山站径流的变化主要由降水主导;向下至高场站、北碚站、寸滩站、武隆站、宜昌站,气温的贡献量超过了降水,居于主导地位。呈现出随着干旱指数增加降水对径流变化的影响增大、气温对径流变化的影响减小的规律。

