受限空间欠采样条件下航空发动机关键截面流场重构方法研究进展

徐笳森 ，郑培英 ，张 轲 ，娄方远

（1.南京航空航天大学航天学院，南京 211106；2.中国航发沈阳发动机研究所，沈阳 110015；3.清华大学航空发动机研究院，北京 100084）

0 引言

航空发动机及燃气轮机的性能评估需要测量关键截面的流体热力参数，针对航空发动机内部复杂、非定常、强不均匀流场，探针的测点布局及基于离散测点的数据分析方法对发动机性能评估有较大影响[1]。当前国内外针对探针沿周向和径向布局（包括探针数目，位置等）缺乏系统的理论指导，还没有一套通用的周向探针优化方法；针对离散探针数据的处理方法及误差机理尚未明确；基于离散数据对发动机关键截面流场实现重构的研究还处在初期阶段。

王振华等[1]强调探针布局对航空发动机及燃气轮机性能评估非常重要，然而当前国内外针对探针沿周向布局（包括探针数目，位置等）依然广泛采用基于工程经验的探针布局方案。在航空发动机的研究工作中，Saravanamuttoo[2]和Pianko 等[3]分别采用沿周向等距、等节距的探针布局，对发动机部件性能以及气动性能进行了探究。此外，针对离散探针数据的处理方法，当前国内外通常基于均值计算。然而，Livesey等[4]、Pianko 等[3]以及Greitzer 等[5]的研究表明，面积平均、质量平均、总焓平均都不能完全代表所有非均匀流场的气动参数或热力参数；其后，Prasad[6]和Cumpsty 等[7]的研究表明，功平均以及推力平均同样无法完全代表所有非均匀流场参数。综上所述，基于传统的探针布局方案及均值处理方法，无法精确评估航空发动机关键截面0 维流场参数。而通过李红丽等[8]、Stummann 等[9]以 及Chilla 等[10-11]等 诸 多 学 者 的 研 究 发现，关键截面流场参数的模糊估计对航空发动机整机及部件性能评估会造成较大误差；Methel 等[12]、白磊等[13]、Seshadri 等[14-15]在进行优化探针位置的研究中，发现提高关键截面流场参数的采样精度可使整机及部件性能评估的准确性有较大提升。例如近期由英国剑桥大学惠特实验室开展的试验研究[10]显示：当采用传统周向均布的探针布局方案及面积均值计算方法评估多级压气机等熵效率时，会造成高达2.8 个点的不确定性和2.8个点的误差。

为解决这一难题，针对航空发动机内强3 维、强不均匀流场，本文采用公开试验数据与高精度仿真相结合的方式系统研究航空发动机关键截面复杂流场关键特征及演变规律；在此基础上通过解析航空发动机内复杂流场的主导特征，探索在受限空间欠采样条件下航空发动机内流复杂流场重构技术及其应用。

1 发动机关键截面典型流场特征

在航空发动机及燃气轮机中，由于受进气畸变、多级压气机级间相互作用、燃烧室热斑的影响，使发动机进口、压气机出口、燃烧室出口、涡轮出口截面的流场具有非定常、强不均匀特性，沿着周向、径向变化。为探明航空发动机及燃气轮机内流动特征，首先基于公开文献，开展系统的管流（进排气系统[16]）与环流（压气机[17-19]、燃烧室[20]、涡轮[21]）气动特征研究，在此基础上，采用高保真度仿真方法对进排气系统、多级轴流压气机、燃烧室、涡轮开展仿真分析。

1.1 典型进气道出口截面流场特征

对于大涵道比民用航空发动机的进气系统而言，在进气道或短舱长度小、无进气畸变的情况下，航空发动机进口流场不均匀度较低。对于军用发动机而言，常采用S 弯进气道，进气道较长，在发动机进口截面会产生总压及预旋畸变，沿周向具有同轴系固有频率相同的分布特征。在此基础上，通过高保真度仿真开展S 型进气道内流场特征研究。仿真分析结果表明，在S 型进气道靠近出口的下壁面存在逆压梯度，原本吸入的附面层加上壁面的粘性作用使得越靠近壁面的气流速度越低。在逆压力梯度与下壁面外扩曲线的双重作用下，流体的冲击力无法抵抗逆压力，将会在下壁面某一处产生回流，回流的流体在分离点处与气流的冲击力达到平衡，又会向壁面法向方向卷起而再次顺流，因而形成大片分离区。靠近上壁面的气流在上下壁面的压差作用下沿着侧壁偏转，而靠近下壁面的回流区为上壁面发展的二次流提供了空间，二次流又会反过来抬起回流区，二次互相加强。所以在进气道出口截面表现为带有“对涡”形式的总压畸变与旋流畸变，沿流向进气道总压、流线分布图谱的发展历程如图1所示。

图1 沿流向进气道总压、流线分布图谱的发展历程

1.2 典型多级轴流压气机出口截面流场特征

对于主要由多级轴流压气机组成的航空发动机压缩系统而言，压气机内流动具有非定常、强3 维、强不均匀特征。公开研究结果[11-12]表明，决定压气机周向流场均匀特征的因素主要为上下游静子尾迹的叠加及相互作用。此外，压气机内流道-流道间的流场具有非周期性，因此基于离散探针数据及周期性流场假设的传统压气机性能评估方法具有较大误差。近期，Chilla 等[11]针对RR 公司8 级核心机压气机内部流场进行了研究，50%叶高截面总压场分布如图2 所示。为了精确模拟多级轴流压气机级与级之间的相互作用，采用半周非定常RANS仿真分析方法。由于级间相互作用包括上下游静子尾迹叠加及势场的相互作用，多级轴流压气机末级出口截面的总压场沿着周向是强不均匀的。尽管如此，压气机流场沿周向不均匀分布特征却有据可循，而且通常由少数几个波数主导。其中，压气机前部和中部的主导波数主要是上游静子叶片数，而压气机后部的主要波数受到出口支板数的影响。以第6 级静子S6 出口50%叶高截面总压场分布为例（如图3 所示），总压力场的周向不均匀分布特征主要由第5级静子S5，第6级静子S6以及之间的相互作用主导。主导波数包括S5、S6，以及S6-S5。

图2 RR公司8级轴流压气机50%叶高截面总压场分布

图3 RR公司多级压气机S6出口截面50%叶高总压分布

此外，基于历史试验数据研究了3 级轴流压气机中第1 级和中间级出口总压场的周向不均匀度[17]。例如，第1、2 级静子S1、S2 出口截面88%叶高处不同流道的总压沿着周向的分布以及相对应的空间频谱分别如图4、5 所示。显而易见的是，S1 和S2 出口总压场沿周向存在显著的不均匀性。不同流道出口的总压分布不尽相同。因此无论是采用单一流道试验测量结果还是基于单一流道及周期性边界条件假设的仿真结果，都会造成较大的压气机性能评估误差。整体而言，由于多级轴流压气机级间相互作用，尤其是静子尾迹的相互叠加及同势场的相互作用，不同流道出口的总压分布不尽相同且分散度较大。然而在试验测量中，通常是基于不同流道内流动一致的假设，沿不同流道不同节距位置布置探针，因此会造成较大的试验性能评估误差，以本研究中的3 级轴流压气机为例，由于流场不均匀及离散探针数据造成的压气机等熵效率评估误差可达到2.3 个百分点，出口总压不均匀度对压气机等熵效率评估影响如图6所示。

图4 第1级静子S1下游88%叶高截面总压场分布

图5 第2级静子S2下游88%叶高截面总压场分布

图6 出口总压不均匀度对压气机等熵效率评估影响

1.3 典型燃烧室出口截面流场特征

燃烧室出口温度分布的不均匀性是影响航空发动机涡轮工作状态的重要参数之一，对涡轮的效率和寿命有着重要的影响。由于受燃烧喷嘴的离散特性和掺混气体的影响，燃烧室出口平面的温度测量显示出大的径向和圆周温度变化，流动具有强不均匀性。通常认为：

（1）燃烧室径向温度不均匀由衬里冷却气流主导。

（2）燃烧室周向不均匀由喷嘴及冷却气流及主流掺混主导。

通常采用温度分布因子（Temperature Distribution Factor，TDF）量化燃烧室出口处的温度不均匀性程度。2 个广泛采用的参数包括径向TDF（RTDF）和整体TDF（OTDF）。RTDF是测量周向平均温度场不均匀性的参数，而OTDF是测量最热斑与平均温度的差异的模式因子。定义为

式中：T3为燃烧室进口温度；T4为燃烧室出口温度，上标area代表区域平均，cir代表周向平均。

Qinetiq 公司测试的军用航空发动机全环形燃烧室出口温度分布如图7 所示[20]。该燃烧室出口平均温度为2072 K，且沿着径向、周向具有强不均匀、非周期特征。基于公开文献[21-23]数据的典型燃烧室出口径向温度分布如图8 所示。从图中可见，燃烧室径向温度分布同燃烧室设计及内衬冷气流量高度相关。不同燃烧室的出口径向温度分布因子形状分散度较大[24]。

图7 军用发动机全环形燃烧室出口温度分布

图8 航空发动机燃烧室典型出口径向温度分布

1.4 典型涡轮出口截面流场特征

对于航空发动机及燃气轮机中的涡轮部件而言，由于燃烧室喷嘴以及冷却射流的离散性，涡轮入口或燃烧器出口温度场本质上有着强烈的不均匀性。涡轮内流场不均匀主要由以下3种因素造成：

（1）燃烧室出口不均匀温度场，即热斑在涡轮中的迁移。

（2）涡轮叶排之间的相互作用，包括静子尾迹的叠加及相互作用。

（3）高压涡轮冷却气流同主流路的掺混。

本文基于高保真仿真方法对1 个典型双级高压涡轮开展了半周非定常仿真分析[25]。涡轮为GE 公司设计的E3-双级高压涡轮。研究内容包括：

（1）燃烧室出口温度场及热斑对涡轮内流场特征的影响。

（2）涡轮内叶排相互作用对涡轮内流场特征的影响。

（3）高压涡轮冷却气流掺混对涡轮内流场特征的影响。

数值模拟所采用的湍流模型为k-ε模型。涡轮的流体域离散化后，在所有端壁/叶片表面上都实现了10~50范围内的y+值。高压涡轮计算域、网格划分及冷却气流孔位置如图9 所示。涡轮冷却采用源项进行模拟。

图9 高压涡轮计算域、网格划分及冷却气流孔位置

高压涡轮进口完美周期性热斑总温分布及真实整机环境总温分布如图10 所示。通过对比具有完美进口周期温度场（图10（a））及具有非周期性进口温度场（图10（b））的2个仿真结果展开分析。高压涡轮进口完美周期性热斑总温分布及真实整机环境总温分布如图11所示。从图中可见，在进口为完美周期性热斑情况下，在高压涡轮入口观察到的交替熵的重复模式对应于周期性入口温度分布；相比之下，当燃烧室出口温度具有非周期特征时，高压涡轮入口处的熵分布周期性较低。随着热斑在高压涡轮叶片行中迁移，熵模式在这2 种情况下都变得更加复杂，这主要是由于叶片行相互作用。对于这2 种情况，在高压涡轮出口处仍然可以看到热斑的足迹，这与公开文献中报告的情况一致。

腰椎管狭窄症作为脊柱外科临床工作的重要组成部分，往往表现出行走间歇性跛行，其诊断往往需要借助于临床影像学（CT、MRI等）检查。Amundsen T等[1]通过临床症状与影像学相关指标分析发现，腰椎管狭窄的程度与患者实际临床症状并没有显著的相关关系。相对于腰椎管狭窄症患者长期存有的腰部疼痛，基于临床症状诊断显得意义不足。

图10 高压涡轮进口完美周期性热斑总温分布及真实整机环境总温分布

图11 高压涡轮进口完美周期性热斑总温分布及真实整机环境总温分布

此外，进口完美周期性热斑情况下50%叶高截面总温按空间和频域的分布如图12 所示。从图12（a）中可见，在高压涡轮入口处具有完美周期性热斑的基线情况下①~⑤的中跨时间平均总温度分布：①位于高压涡轮入口处，沿圆周方向的温度变化为61.5 K，相当于沿周向平均总温度的7.9%。热斑在第1 排叶片中几乎没有衰减，只有约12.3°的轻微相移。与定子排相比，热斑在转子叶排迁移过程中衰减得更多。

图12 进口完美周期性热斑情况下50%叶高截面总温按空间和频域的分布

总体而言，热斑在接近高压涡轮出口时明显衰减，环向温度变化的绝对值降至39.6 K，占当地平均总温度的8.7%。此外，当入口热斑穿过高压涡轮时，圆周温度不均匀性的驱动机制也在演变。在高压涡轮入口（截面①），中跨处的周向不均匀性主要由波数为18 的热斑主导，从而形成极佳的正弦形状。然而，在高压涡轮出口处，更多影响因素包括高压涡轮叶排间相互作用对圆周温度不均匀性作出了贡献。

为了研究圆周温度不均匀性的驱动机制，进行了空间快速傅立叶变换（Fast Fourier Transform，FFT），进口非周期性热斑情况下50%叶高截面总温按空间和频域的分布如图13所示。从图13（b）中可见，正如预期的那样，热斑（波数Wn=18）压倒性地控制了高压涡轮入口温度圆周不均匀性。在S1 的出口（截面②），可以观察到S1 的影响，由1 个波数为46 的小峰表示。在1 级转子R1 的出口（截面③），也可以观察到S2 的势场，由Wn=48 的小峰表示。值得注意的是，频谱图没有任何与转子叶片排相关的波数。

图13 进口非周期性热斑情况下50%叶高截面总温按空间和频域的分布

这是因为流场是时间平均结果，所以通过平均消除了转子小波数的存在，模拟了使用稳态探头测量总温度的场景。

从图13 中可见在高压涡轮入口处具有非周期性热斑的Qinetiq 情况下截面①～⑤的时间平均总温度分布。燃烧器与燃烧器之间不对称的存在不会影响热斑迁移的总体趋势，例如热斑的幅度在转子上比在叶片排或定子上衰减得更多。然而，燃烧器到燃烧器的不对称性会在空间域中产生更分散的能量分布（图13（b））。尽管热斑分量（Wn=12）是高压涡轮入口温度圆周不均匀性的主要贡献者，但是当入口热斑在高压涡轮上迁移时，定子排的尾流和电势会导致温度圆周不均匀（图13（b））。此外，在高压涡轮出口处有1个很强的低阶分量（Wn=2），这很可能是由所选的半环模拟策略引起的混叠分量。

2 基于多波束的流场重构方法

理论上空间周期为2π 的半径为R的任意截面处的稳态流场可以用不同波数的无限序列来描述

式中：x(θ)为沿圆周方向的流动特性；co为信号的直流分量；Wn,i为第ith个波数；Ai和φi为信号的幅度和相位。

此外，定义ai=Aicosφi和bi=Aisinφi，式（3）可以转换为

2.1 多波束近似方法

因此，压气机中的圆周流动可以用N个主导波数来近似

这是重建圆周流场的重要一步，因为式（3）中未知系数的数量从无穷大减少到了2N+1个。

为了求解包含2N+1 个未知数的方程，需要在不同圆周位置测量的最少相同数量的数据点，θ=(θ1,θ2,θ3,…θm)。该系统可以描述为

式中：A为设计矩阵，维度为m×(2N+1)；F为包含2N+1个未知系数的向量；x为包含来自不同圆周位置的所有m个测量数据点的向量。

A、F和x的数学表达式为

求解式（4）中描述的N个感兴趣的波数。向量x中数据点的个数必须大于未知系数的个数，或者m≥2N+1。然而，在实践中，由于x(θ)的不确定性，重建信号显得至关重要，它包含误差，评估重建信号的置信度。这些都需要x(θ)中的额外数据点。因此，至少需要2N+2个测量点来表征N个感兴趣的波数。然而，这会产生1 个方程多于未知数的超定系统。在本研究中，最小二乘拟合方法用于求解式（6）中的未知系数。

有了所有主导波数的幅度和相位，可以使用式（5）来重构圆周流场。使用多波束近似方法利用空间欠采样数据重构航空发动机典型部件关键截面流场的技术路线如图14所示。

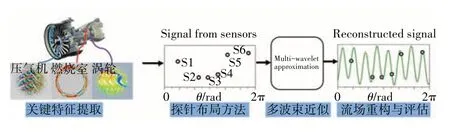
图14 基于多波束方法航空发动机内复杂流场重构技术路线

2.2 条件数

采用多波束近似方法重建的流场容易因探头测量或探头定位的不确定性而导致x(θ)误差。在式（6）描述的线性系统中，重构信号中的误差受设计矩阵A的条件数k的影响。设计矩阵的条件数定义了F中相对误差相对于x中的相对误差的上限，即

设计矩阵条件数的变化范围可以为1~∞。具有大条件数的系统会导致重构信号中的过大误差。矩阵条件数的计算公式有多种，本文采用二范数进行向量和矩阵范数计算。条件数的计算公式为

式中：A+为方阵A的Moore-Penrose伪逆。

在本研究中，设计矩阵A的条件数由探头位置θ和感兴趣的波数Wn确定。知道感兴趣的波数后，设计矩阵的条件数描述了探针在捕获感兴趣波数方面的分布情况。这是选择探头位置的最重要参数，是下一节讨论的重点。因此，以确保条件数较小的方式选择圆周位置θ，这是利用遗传算法来实现的。选择200 的种群大小和200 的迭代次数，优化的执行将在几秒钟内完成。值得注意的是，由于遗传算法的随机性，每次优化运行都可能导致不同的最小值。虽然这里没有详细说明，但本文将讨论条件数的影响。

为了评估重建信号的置信度，使用皮尔逊相关系数或皮尔逊r，并计算

式中：x（θ）为测量的真实信号；xfit,j(θ)为重建信号；皮尔逊r的范围在0～1 之间，对于重构良好的圆周流场，预测的流动特性应与所有测量位置的实际值一致，并且皮尔逊r的值接近1，反之亦然。

本文主要对方法论进行概述，详细方法论证详见文献[26-27]。

3 试验验证

相关探针布局及流场重构技术在评估航空发动机多级压气机出口截面总压分布、燃烧室出口温度因子、高压涡轮出口截面总温分布的应用中得到初步试验验证。

3.1 多级轴流压气机总压场重构

该探针布局优化方法及流场重构技术在普渡大学叶轮机械试验室3 级轴流压气机中得到验证[17]。该3 级轴流压气机能够模拟航空发动机核心机末级压气机的流动特征（马赫数及雷诺数）。采用该方法优化的探针布局，仅用<20%的流场信息实现了第1、2 级静子下游总压场的重构，多级轴流压气机出口总压场场重构结果同真实值对比如图15 所示。重构流场计算得到的均值与真实值之间的误差小于0.1%，第1、2 级静子下游不同叶高处基于重构流场计算得均值总压与真实值比较见表1。

表1 第1、2级静子下游不同叶高处基于流场重构的总压值与真实值对比

图15 多级轴流压气机出口总压场场重构结果同真实值对比

3.2 燃烧室出口总温场重构与温度因子评估

该探针布局优化方法及流场重构技术在Qinetiq公司测试的典型军用航空发动机全环形燃烧室上进行了验证[24]。典型全环形燃烧室出口温度试验结果与重构结果之间对比如图16所示。基于公开文献[9]数据，该燃烧室出口平均温度为2072 K，且沿着径向、周向具有强不均匀特征，如图16（a）所示；采用该方法优化的探针布局，仅用沿周向10 个位置的测量数据实现了燃烧室出口温度场的重构，如图16（b）所示。基于重构温度场计算得到的径向温度分布（RTDF）与真实值（由周向144测点计算获得）误差小于0.5%，如图16（c）所示。

图16 典型全环形燃烧室出口温度试验结果同重构结果之间对比

3.3 高压涡轮出口总温场重构

该探针布局优化方法及流场重构技术在美国GE公司设计的E3高压涡轮上进行了验证[20]。E3高压涡轮为2 级带冷却结构。采用该方法优化的探针布局，仅用周向8 支探针的测量数据实现了高压涡轮出口温度场的重构，重构流场计算得到的均值同真实值之间的误差小于0.3%，如图17所示。

图17 E3高压涡轮出口温度场重构结果与真实值对比

4 总结

（1）由于受整机环境下几何特征对探针位置的限制以及整机环境下3 维流动等因素影响，通过有限的测点数据准确获取整机关键测试截面参数非常困难。目前应用比较广泛的航空发动机关键截面探针布局方案针对发动机不同截面流场特性，在进口截面多采用沿周向均匀分布探针布局方案，在级间关键截面采用与上游静子阶梯型布置/等节距方案，但这种布局往往不能体现发动机整机的流场特征。为了解决这一难题，针对航空发动机内强3 维、强不均匀流场，介绍了一种受限空间欠采样条件下航空发动机内流复杂流场重构技术。

（2）依据整机环境下不同部件截面的几何特性，结合文献及数值仿真，开展系统性的管流（进排气系统）与环流（压气机、燃烧室、涡轮）气动特征研究，形成整机环境下各部件关键截面特征提取方法，总结各部件关键截面参数变化规律。

（3）探明了主导航空发动机内流场不均匀特征的内在机理，即航空发动机内流场不均匀特征往往由少数几个波数主导。基于以上发现，介绍了“多波束近似”的方法，该方法在重构多级压气机出口截面总压分布、燃烧室出口热斑分布、高压涡轮出口截面总温分布取得初步试验验证。