考虑卡箍预紧状态的空间管路3维有限元建模
季文豪 ,孙 伟
(1.东北大学机械工程与自动化学院,2.航空动力装备振动及控制教育部重点试验室:沈阳 110819)
0 引言
航空发动机管路系统是流体介质的输送通道,是发动机能量供给系统的重要组成部分[1-2]。除少数管路直接与机匣或其它附件相连外,大多数管路通过卡箍与机匣连接,由发动机转子产生的激振力会通过机匣传递给管路,从而引起管路系统的振动[3]。
为了提高管路系统的稳定性和可靠性,通常要对管路系统的动力学进行分析和设计,而有限元法具有较好的适用性一直是管路系统动力学建模最主要的方法。侯文松等[4]利用管单元创建了L形管的有限元模型,对充液管路进行了固有频率分析;赵伟志等[5]利用管单元创建了空间管路的有限元模型,并对燃油管路进行了固有特性和振动模态分析;Gao等[6-7]使用梁单元创建了平面管路的有限元模型,对单管和并联管路进行了模态分析;Chai 等[8]使用梁单元创建了L形管的有限元模型,并进行了模态分析和基础激励条件下的振动响应分析。在上述管路系统动力学建模中,主要用管或者梁单元模拟管路的力学特性,对求解管路系统固有特性或者指定位置的振动响应可行,但是在求解管路动应力时,使用这种简化单元通常不能获得准确的动应力,为此,考虑使用3 维实体单元创建管路的有限元模型并进行动应力求解。在实际的管路系统有限元建模过程中,对卡箍约束的模拟是建模的关键。在大多数研究中采用弹簧单元模拟卡箍的力学特性。Liu 等[9-10]用弹簧组模拟卡箍约束,其中弹簧组的卡箍刚度按照半正弦分布;Li等[11]使用悬臂梁模拟卡箍的力学特性;徐培元等[12]使用2 个沿着管路径向分布的弹簧模拟卡箍的力学特性;黄益民等[13]用等效质量和6 个方向的弹簧单元模拟卡箍支撑;李枫等[14]通过设置接触的方式模拟卡箍和管路的连接;Tang 等[15]使用沿着径向分布的2 个弹簧模拟卡箍支撑。上述对卡箍的模拟研究中,没有将卡箍的预紧方式与建模方法直接关联,具有一定的局限性。
本文基于ANSYS 平台,采用卡箍力学特性的模拟方法构建了管路系统的有限元模型,采用该模型分析了简谐激励条件下管路系统的应力响应,并进行了试验验证。
1 卡箍预紧分析及力学模拟方法
卡箍通过螺栓连接在底座上,如图1 所示。卡箍受到螺栓的预紧力作用,可以通过分析卡箍的受力状态来定性描述模拟卡箍力学特性的弹簧单元刚度分布规律。

图1 卡箍安装
1.1 卡箍预紧分析
选择卡箍支撑处的管路为研究对象,假设卡箍对管路的力是沿着接触面分布的,则管路受到卡箍的力分析如图2所示。

图2 管体受到卡箍的力分析
图中:Fy1和Fy2分别为卡箍上箍带和下箍带受到的预紧力传递给管路产生的竖直方向的均布夹持力;Fx1、Fx2和Fx3为卡箍1,2,3 区箍带给管路的水平方向的夹持力;假定2 区和3 区的管体部分径向变形量相等,均为ΔR;进一步假定管路上任意一点沿着径向的刚度相等,参照图2 中的单点受力,针对2 区和3 区中任意一点有
式中:α、β分别为2 区和3 区上的卡箍与管路的接触点位置角,即过接触点连接管路中心形成的直线与竖直方向的夹角。
另外,针对任意1 根给定的管路,由卡箍螺栓预紧力可以得到Fy1和Fy2
式中:Qp为螺栓的预紧力,与螺栓的公称直径有关,可视为已知量;nu、nd分别为后续有限元建模时卡箍上箍带和下箍带与管路的接触区在圆周方向上划分的节点数,针对具体管路也可视为已知量。
从图2 中可见,卡箍的上箍带接触面积大致为下箍带接触面积的2倍,所以有
结合式(1)、(2)可以得到2 区和3 区上的管路受到的水平方向夹持力Fx2和Fx3
分析1区部分卡箍给管路的x方向的夹持力。因为卡箍结构的特殊性,卡箍下箍带传递给管路的力会产生附加的x方向的夹持力,由管路x方向的受力平衡可得到1区任意接触点处受到的x方向的夹持力Fx1
基于式(5)~(8)获得的水平及竖直方向的夹持力,可确定后续模拟卡箍力学特性的弹簧单元刚度值的分布规律。
1.2 卡箍力学特性的模拟
创建管路的有限元模型后,在卡箍与管路接触区的首末两端分别采用弹簧组模拟卡箍的力学特性(如图3所示),即每个卡箍用2个同面弹簧组来模拟。而每个弹簧组中各弹簧的刚度值分布可借鉴第1.1节的卡箍预紧分析结果。

图3 卡箍力学特性的模拟
可以认为卡箍x方向和y方向的夹持力与模拟卡箍力学特性的弹簧单元刚度成正比,则参照式(5)~(8),有
式中:ky1和ky2分别为模拟卡箍力学特性的y方向上的弹簧单元刚度;kx1、kx2和kx3为模拟卡箍力学特性的x方向上的弹簧单元刚度。
从式(9)~(12)中可见,虽然模拟卡箍的弹簧单元的刚度有5 个待定值(ky1、ky2、kx1、kx2和kx3),但它们之间存在确定的函数关系,因而只需要指定任意一个方向的弹簧刚度,例如ky2,即可确定所有的模拟卡箍力学特性的弹簧刚度。
2 管路系统有限元建模
采用实体单元SOLID186模拟管体,并使用第1.2 节中描述的方法模拟卡箍约束。空间管路CAD模型如图4 所示,图中,Lh1和Lh2分别为卡箍1、2 的安装位置,L1为直线段1-2的长度。
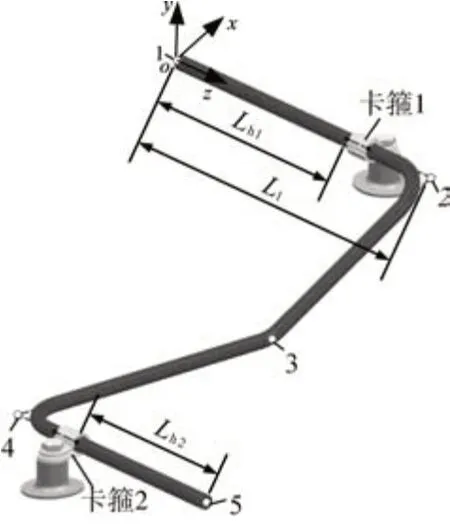
图4 空间管路CAD模型
2.1 构建管路的几何模型
利用管路关键点(图4中的点1~5)的坐标在ANSYS中建立管路关键点,按顺序连接关键点并使用“LFILLT”命令生成折弯圆弧中心线,从而得到管路中心线。绘制管路截面尺寸图,使用“VDRAG”命令扫掠得到管路的几何模型,如图5(a)所示。

图5 实体单元管路系统有限元建模
2.2 对管体进行网格划分
选用SOLID186 实体单元对管路进行网格划分,分别设定直线段和圆弧段的单元长度以及管路截面上的单元数量,使用扫掠分网的方式进行网格划分,得到的结果如图5(b)所示。
2.3 引入卡箍约束
卡箍约束使用第1.2节中描述的卡箍力学特性的模拟方式,在卡箍区左右端2 个作用面相关的节点上创建弹簧单元,指定弹簧刚度即可得到最终的有限元模型,具体结果如图5(c)所示,模拟卡箍力学特性的弹簧组局部放大如图5(d)所示。
3 实例分析
航空发动机管路系统在实际工作过程中承受多种激振力的综合作用,其中冷端风扇机匣的外部管路承受简谐激励作用,为了提高管路系统的稳定性和可靠性,需要分析管路系统在简谐激励作用下的振动响应。这里分别利用第2 章中提出的实体单元有限元建模方法和常规的管单元有限元建模方法对实际管路进行模态分析和谐响应分析,并通过试验加以验证。
3.1 试验装置
以2 根实际的空间管路为研究对象,对应图4 中的关键点坐标见表1。测量管路系统固有频率时的卡箍位置见表2,测量管路系统简谐激励条件下振动响应的卡箍位置见表3。
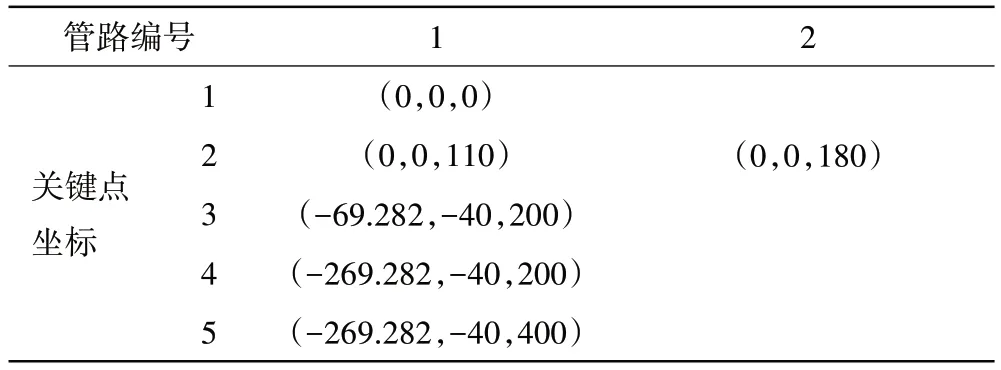
表1 管路的关键点坐标 mm

表2 测试固有频率时的卡箍位置 mm

表3 谐响应分析的卡箍位置 mm
根据表2、3 的卡箍位置,组建对应的固有频率测量装置以及简谐激励条件下的振动应力响应测量装置。其中固有频率测量如图6 所示。根据卡箍安装位置安装管路,使用3 向加速度传感器PCB356A01测量加速度响应,并利用锤击法测量管路系统的固有频率。其中力锤为PCB086C01,数据采集装置为LMS 8 通道便携式数据采集前端。

图6 固有频率测量
对于简谐激励条件下振动应力响应的测量,这里采用电测法,利用应变花和惠斯通电桥测量管路系统的应力响应。简谐激励条件下的应力响应测量现场如图7 所示。在测点A 处贴敷一片BE120-1CAQ30P400应变花,并在1 根不受力的管路上贴敷相同的应变花作为温度补偿片,采用邻边半桥的接线方式,在调节电桥平衡后测量应变片的输出。使用东菱LTT1212 振动台对管路施加简谐激励,并使用LMS 8通道便携式数据采集前端实现数据采集。

图7 简谐激励条件下的应力响应测量现场
3.2 动力学分析
3.2.1 固有频率分析
选定管路外径 ,壁厚1 mm,折弯半径24 mm,管路的材料参数:密度7850 kg/m3,弹性模量2.04×1011Pa,泊松比0.285。卡箍安装处的螺栓拧紧力矩为7 N ⋅m,使用实体单元模拟管体时,通过反推辨识的方式得到模拟卡箍下箍带弹簧刚度为ky2=4280 N/m,由式(9)可以得到模拟卡箍上箍带弹簧刚度为ky1= 2140 N/m,而模拟卡箍力学特性的x方向的弹簧刚度可以通过式(10)、(11)和(12)获得。使用管单元模拟管体时,选择弹簧的线刚度为42000 N/m,扭转刚度为50 N⋅m/rad。利用试验方法(图6)测量2根管的固有频率,与仿真分析结果进行对比,结果见表4。

表4 管路固有频率 Hz
从表中可见,使用实体单元进行固有频率分析得到的前3 阶结果均和试验结果接近,偏差都小于6%。而使用管单元模拟管路系统时,第1 阶固有频率和第3 阶固有频率较为准确,偏差均为6%左右,但是第2阶固有频率相差较大,约为10%。可见,使用本文提出的管路系统3 维有限元建模法进行固有频率分析能够能得到更加准确的结果。
3.2.2 简谐激励条件下的应力响应分析
利用振动台对管路系统施加y方向的基础加速度激励(图4),幅度为1g,测试2 个管路的振动应力。管1 选择的测点远离卡箍,位于管路的直线段3-4 上(图4),距离关键点4 为100 mm,贴片角度为0°、45°和90°。管2 的测点靠近卡箍2(图4),贴片角度为-45°、0°和45°。需要说明的是,应变片的贴片角度是以管路中心线为基准的,即贴片位置和管路中心线平行时,贴片角度为0∘。试验得到的应变测试结果及计算得到的主应力结果见表5,表中的σ1和σ3分别为第1、3 主应力,ε0、ε45、ε-45、ε90分别为0°,45°,-45°,90°应变。
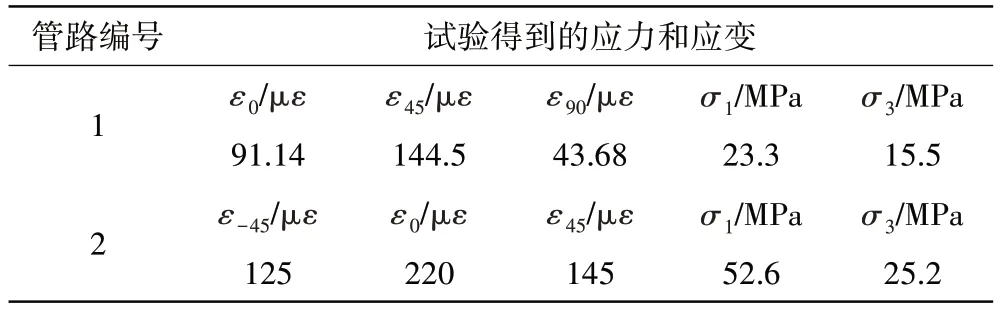
表5 试验得到的应变测试结果及计算得到的主应力结果
基于ANSYS 软件分别使用本文提出的考虑卡箍预紧的3 维实体单元有限元建模方法和常规的管单元有限元建模方法对2 个管路系统进行分析,得到在简谐激励条件下的管路系统的等效应力,如图8 所示。从图中可见,用2 种单元模拟管体时得到的应力分布大致相同,最大应力均位于卡箍2 处。考虑到卡箍安装处为接触区,应力测量的精度较差,因而这里2 号管选择的测点为最大应力点,而1 号管的测点远离最大应力点。将测点处仿真分析得到的等效应力与试验获得的等效应力进行对比,见表6。

表6 仿真分析与测试获得的等效应力对比

图8 用2种单元仿真分析获得的2个管路的应力
从表中可见,使用管单元模拟得到的应力响应结果和试验值相差较大,而使用实体单元模拟管路进行应力响应分析得到的结果更加贴近试验值。另外,测点位置不同时,使用实体单元得到的应力响应结果和试验测试结果的偏差不同,当测点靠近卡箍支撑区时,偏差为19.3%,当测点远离卡箍支撑区时,偏差为18.3%,但是两种情况的响应偏差都小于20%,因而可认为本文提出的考虑卡箍预紧状态的管路系统3 维有限元建模方法能够满足实际的需要。
4 结论
(1)提出一种考虑卡箍预紧状态并用弹簧组来模拟卡箍支撑的建模方法。通过分析上下箍带对管路的夹紧力,确定了模拟卡箍的弹簧单元刚度值分布规律。结果表明,卡箍不同位置处的水平和竖直方向的刚度存在比例关系,且比例关系与位置角和方向有关。
(2)给出了用实体单元并引入上述卡箍约束的有限元建模流程。这种建模方式真实地反映了管路的几何特征和卡箍的约束状态,因而能够适应管路系统动应力求解的需求。
(3)在对2 个管路进行模态分析和谐响应分析时,使用实体单元模拟管体可以得到更加贴近试验值的结果,仿真计算与实测的振动应力偏差小于20%,验证了本文提出的考虑卡箍预紧状态的管路系统3维有限元建模方法的有效性。

