基于K近邻非参数回归的压痕弹性模量估计
金宏平
(湖北汽车工业学院 机械工程学院,湖北 十堰 442002)
传统的拉伸试验作为主要试验手段常用于材料的性能测试,具有试验过程简单、直观的特点,但需要耗费大量的时间制作标准试样来进行破坏性试验,而且易受多种因素的影响导致重复性较差。压痕试验类似于拉伸试验,通过连续采集载荷-位移数据,利用相应的理论对数据进行处理来获取材料的性能。压痕试验不需要制备大尺度的试样,试验过程简单,对零部件表面的损伤较小,能在一定程度上代替现有的拉伸试验,特别是在微小尺度的材料领域和在役设备性能检测上能获取相关材料的力学性能。由于材料与压头的接触变形中呈现大量的非线性过程,根据载荷-位移曲线数据并不能直接获取材料的力学性能。大量学者利用压痕试验、有限元仿真分析和量纲分析等手段和方法进行了材料性能的反演研究[1-3]。Dao 等[4]对76 种弹塑性材料进行了有限元仿真分析,研究表明,采用尖压头能够辨识出材料的力学性能。Yan等[5]采用量纲分析和有限元仿真对尖压头进行了压痕分析,研究结果表明,采用3种不同的尖压头进行压痕试验能获取较高精度的力学性能指标。石文超等[6]利用量纲法确定了铝基复合材料应变强化指数和初始特征应力,采用纳米压痕试验获取铝基体载荷-位移曲线,利用有限元迭代的反演分析法能确定铝基体特征应力和特征应变参数。随着神经网络和机器学习的迅速发展,不少学者也将这些理论和方法应用在压痕试验领域[7-9]。孙明成等[10]采用有限元仿真建立了奥氏体不锈钢的压痕曲线数据库,利用神经网络和优化函数能快速有效获取材料的力学性能指标。通过有限元仿真建立数据集,Weng等[11]采用支持向量回归机建立了代理模型来关联输入(应力-应变函数常数)和输出(预测结果与测量结果之间的平均误差)之间的关系,利用尖压头获取了灰口铸铁的应力-应变曲线。Ghanbari等[12]对铝合金材料进行了大量的仿真模拟并对压痕载荷-位移曲线进行分析,利用神经网络实现了残余应力、屈服强度和硬化指数的有效估计。Huang 等[13]采用迭代有限元模拟和模拟退火群粒子优化方法,通过多重加载-卸载曲线获取了应变硬化指数和应变硬化速率等力学性能。K 近邻回归是根据Cover等[14]提出的K近邻分类方法改进而来,主要思想是对测试样本周围的K个近邻数据进行平均来预测其输出值。由于K 近邻回归的算法简单、鲁棒性好,在回归问题中应用较广泛。球压头在压痕试验过程中,没有尖压头的几何相似性,而且被压材料与球压头在接触变形过程中,材料经历明显的弹性变形、弹塑性变形和塑性变形3个变形阶段,因此采用球压头进行压痕试验具有明显的优势。为此,文中采用球压痕技术和K 近邻算法,拟从大量的压痕试验数据中回归得到材料的压痕弹性模量。
1 球压痕试验的基本原理
在球压痕试验过程中,利用高精度载荷和位移传感器连续采集加载和卸载过程的载荷-位移数据,得到如图1所示的曲线。根据载荷-位移曲线,通过数学计算可得到各种参数,如加载斜率、卸载斜率、最大加载力Fm、最大压入深度hm、残余压痕深度hr等。结合接触力学、弹塑性理论和量纲分析等相关理论与方法,可建立材料力学性能与这些压痕参数之间的关系,从而获取材料的力学性能,如弹性模量E、屈服强度、硬化指数、残余应力等。
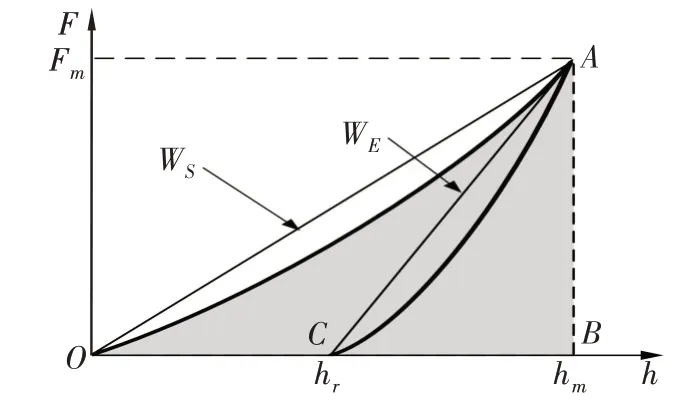
图1 压痕的载荷-位移曲线示意图
在压痕试验的加载过程中,定义外力所施加的能量是压痕加载功Wt,如图1 所示的加载曲线OA与水平位移轴所确定的面积,即
在卸载过程中,被压材料的弹性变形施加在压头上产生弹性恢复功We,如图1 所示的卸载曲线AC与水平位移轴所确定的面积,即
加载曲线OA和卸载曲线AC所围的区域是材料塑性变形所消耗的能量,即压痕塑性功:
在图1中,定义△OAB的面积是绝对加载功WS,即
定义绝对弹性恢复功WE是△ABC的面积,即
同样,△OAC的面积是绝对压痕塑性功:
采用有限元分析软件ABAQUS 进行球压痕的仿真分析。球压头简化为半径是0.794 mm 的刚体,被压材料简化为轴对称结构,最大压痕深度为10 μm。选择弹性模量与屈服强度的比值范围是30~1000,泊松比ν取0.3,硬化指数n分别取0、0.1、0.3和0.5,共60种材料参数模型。
为了提高材料压痕弹性模量的回归精度,利用压痕试验的载荷-位移曲线,通过拟合和积分等数学方法来计算压痕参数。根据对压痕参数的数据进行相关性分析,选择9个无量纲压痕功We/Wt、Wp/Wt、Wp/WS、Wp/WE、Wt/WR、Wt/WE、WR/WS、WR/WE、WE/WS和无量纲压痕弹性模量Eh2m Fm作为样本的特征参数。相关性矩阵如图2所示。从图2中可以看出,虽然Eh2m Fm和Wp/WE、Wt/WE以及WR/WE均呈线性正相关性,但由此并不能唯一确定材料的压痕弹性模量,有可能存在多种材料的Wp/WE、Wt/WE以及WR/WE均相同[5]。其余6个参数均与Eh2m Fm非线性相关。如果建立这些参数之间的映射关系,即可通过压痕试验获取相应材料的压痕弹性模量。有些学者采用多项式拟合的方式来建立压痕参数之间的非线性模型,但该模型易受人为因素的影响,导致其精度和适用范围受到一定的影响。为此,选择上述10个无量纲参数作为K近邻的样本数据以增加样本数据的维度,从而提高非参数回归的准确性。流程如下:首先通过仿真或试验获取球压痕的载荷-位移曲线,计算各压痕参数,建立球压痕参数数据库;然后对数据归一化,并确定K 近邻的K和距离模式,采用K近邻非参数回归得到无量纲压痕弹性模量;最后根据Fm和hm计算压痕弹性模量E。
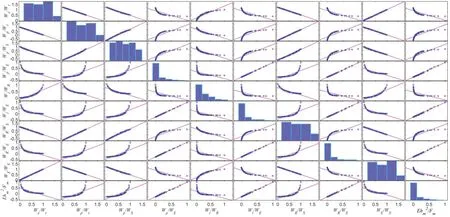
图2 压痕特征参数的相关性矩阵
2 K近邻非参数回归算法原理
常用的回归模型是基于数据分布的假设,而在实际应用中很少有满足这种假设的情况。而K 近邻回归不需要考虑数据分布,仅仅是通过训练数据来进行预测。因此,K近邻回归算法能有效处理线性和非线性问题,尤其在高维空间。
假设训练数据集有N对数据,表示为
式中:Xi为训练样本集的第i个输入样本数据,维度是m维空间为第i个样本的第j个特征参数,对应的输出值为yi。
根据K近邻算法(KNN)的定义,测试样本X与训练样本Xi的相似关系是通过计算特征参数之间的距离来进行判断,通常采用欧式距离:
欧式距离是最常用的用于判断2 个样本相似性的距离测度,但并不是在每个领域都最优。有些学者采用曼哈顿距离来判断2个样本的相似度:
将X与Xi的距离按从小到大排序,找到距离最近的K个样本,并将对应的输出yi进行数值平均,即可回归得到测试样本的输出估计值ŷ:
从式(10)中可以看出,K 近邻回归存在一些问题,如所有近邻具有相同的权重时K如何确定以及距离模式的选择等。一些学者对K 近邻算法进行了改进,如加权K 近邻算法(WKNN)[15],通过改变近邻的权重来提高K 近邻算法的可靠性和准确度。回归得到测试样本的估计值ŷ采用式(11)计算:
式中:wi为第i个近邻训练样本对测试样本影响的权重,与训练样本和测试样本的距离相关。从式(12)中可以看出,距离测试样本越近的训练样本权重越大,对测试样本的影响越大。
Keller 等[16]采用模糊数学理论,通过引入隶属度来处理不确定性的问题,提出了模糊K近邻算法(FKNN)。权重的计算公式为
式中:m为模糊强度系数,一般选择2。
有学者采用高斯K 近邻算法(GKNN)[17]计算训练样本对测试样本的影响权重:
式中:a为高斯峰值,一般选择2;σ为标准方差,一般设定为0.5。
上述4种K近邻算法的权重w与距离d的变化关系如图3所示。从图3可以看出,KNN算法对于K个近邻训练样本的权重相同,均为1。当测试样本和训练样本的距离小于单位长度时,FKNN算法中训练样本对测试样本的影响权重远大于WKNN算法的权重;当训练样本与测试样本距离大于单位长度时,FKNN 算法的权重小于WKNN 算法的权重。从式(12)~(13)也可以看出这种变化关系。而对于GKNN算法,当距离小于0.1时,权重基本不变;当距离大于1后,权重迅速减小。
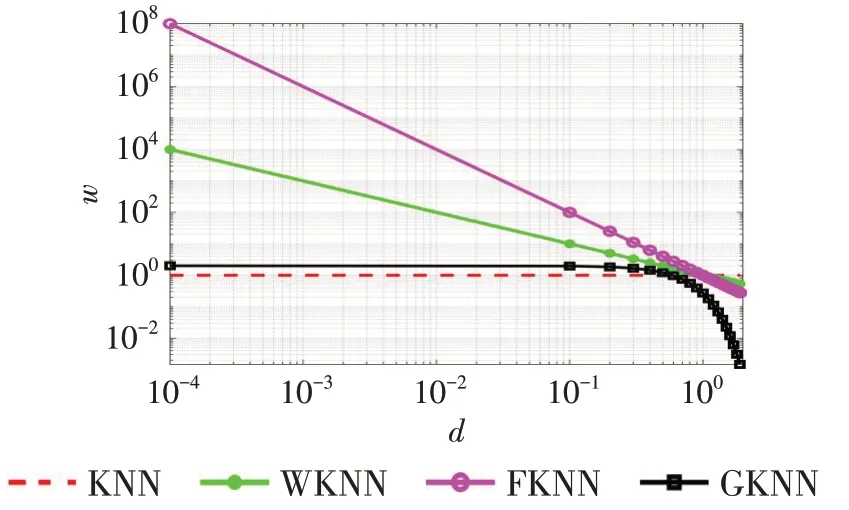
图3 不同K近邻算法的权重与距离关系图
3 结果分析
将60个有限元仿真分析得到的数据样本进行归一化后,再随机分成42个训练样本和18 个测试样本,分别对4种K近邻算法进行测试分析。在使用K近邻非参数回归压痕弹性模量过程中,分别采用曼哈顿距离和欧氏距离模式以及近邻数K的变化范围1~9。为评估回归性能,采用均方根误差(RMSE)作为评价指标:
式中:yi为测试样本真实值;ŷi为测试样本估计值。
分别采用曼哈顿距离和欧氏距离来分析K对回归性能的影响,结果如图4 所示。当K为5 时,4种K 近邻算法的RMSE 均为最小。随着K增加,4种近邻算法的回归效果变差。而KNN 算法的RMSE变化最剧烈,说明近邻点的影响程度对回归精度影响较大。当近邻点选取较多时,较远的近邻点对回归值也有影响,降低了回归精度。当近邻数大于1 时,FKNN 算法的RMSE 变化较小,可见,采用模糊理论的隶属度概念能提高K 近邻算法的回归性能。从图4中也可以看出,采用曼哈顿距离的RMSE 比采用欧氏距离的RMSE 小,即采用曼哈顿距离的K近邻算法的回归性能较好。可见,在估计压痕弹性模量时,采用曼哈顿距离能获得更高的精度。因此文中采用5 近邻和曼哈顿距离的模糊K近邻算法来估计压痕弹性模量。
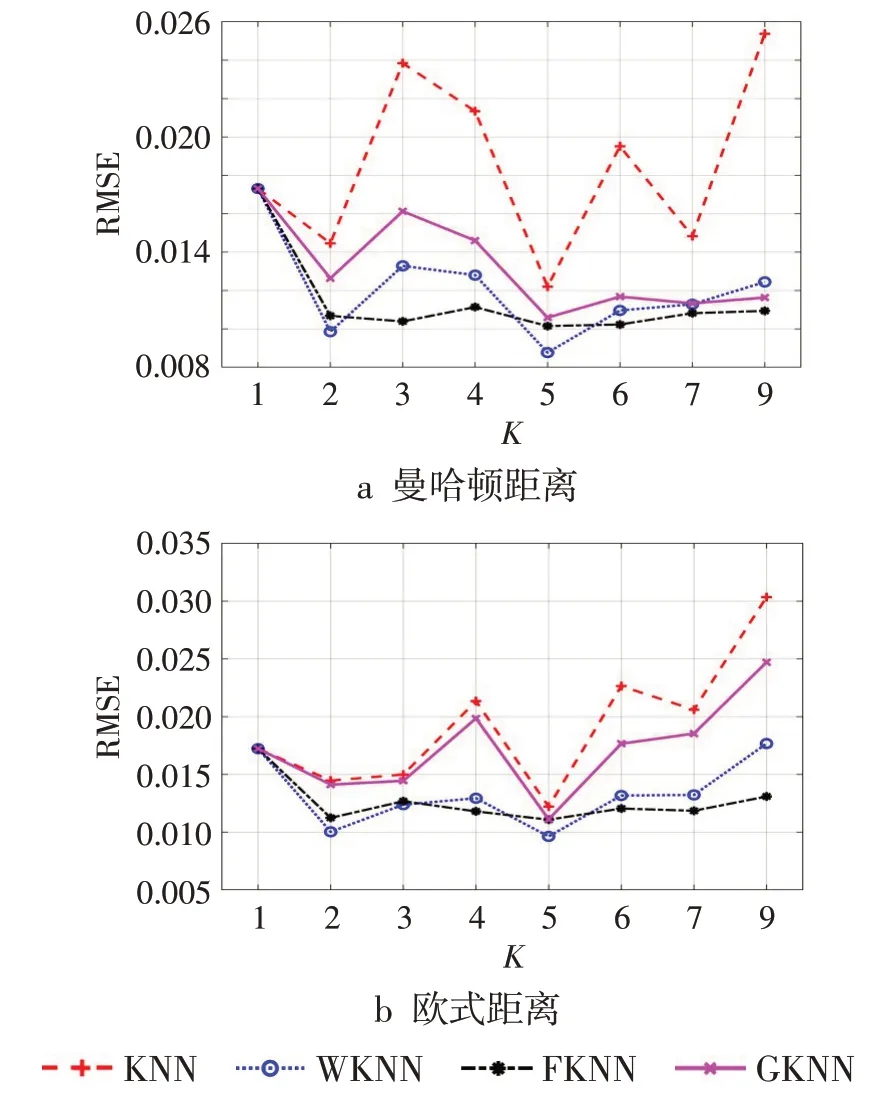
图4 K对回归精度的影响
图5 反映了当K为5 时采用曼哈顿距离的FKNN 算法的效果,可以看出,采用曼哈顿距离的FKNN 算法估计出的无量纲压痕弹性模量参数Eh2m Fm精度较高,只有第9 个的测试样本偏差较大,达到9%,主要原因是该样本的特征与其他样本的特征差异较大,属于离群点。根据压痕试验的参数Fm、hm,利用回归得到的无量纲压痕弹性模量Eh2m Fm,可计算得到压痕弹性模量。
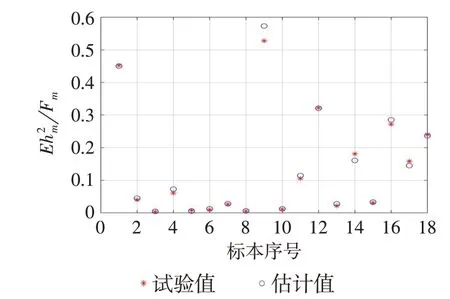
图5 FKNN算法的试验值与估计值对比
4 结论
在球压痕试验过程中,被压材料与球压头存在接触变形、材料弹塑性变形和几何变形等非线性变形。采用拟合的方式来建立压痕参数之间的非线性显式模型,易受人为因素的影响,导致其精度和适用范围受到一定的影响。K 近邻回归通过训练数据来进行预测,能有效处理线性和非线性问题。文中通过有限元仿真分析和相关性分析,建立了无量纲压痕功和无量纲压痕弹性模量的数据集。仿真结果表明,相对于K 近邻算法、加权K 近邻算法和高斯K近邻算法,采用5近邻和曼哈顿距离的模糊K近邻算法来估计压痕弹性模量,能够获得较高精度的压痕弹性模量。后续将通过收集试验数据来进行验证。

