Chaotic opposition initialization and average mutation update-based differential evolution
FU Junhao,LI Ting,GE Hongwei
(1.School of Artificial Intelligence and Computer Science,Jiangnan University,Wuxi 214122,China;2.Jiangsu Provincial Engineering Laboratory of Pattern Recognition and Computational Intelligence,Jiangnan University,Wuxi 214122,China)
Abstract:The diversity of individuals affects the quality of the solution sets and determines the distribution of the solution sets in solving multi-objective optimization problems.In order to expand the search direction of individuals,increase the diversity of the population and avoid individuals from gathering at the boundary during the mutation process,a chaotic opposition initialization and average mutation update-based differential evolution (COI-AMU_DE) is proposed.Firstly,in order to generate a uniformly distributed initial population,random numbers are subjected to tent chaotic map and opposition-based learning in the initialization process to generate uniformly distributed random numbers.Secondly,a mutation operator is processed to avoid individuals from gathering at the boundary to improve the diversity of population.In each iteration,the average mutation update of the individuals is carried out for legalization,and the weighted sum of the rankings based on the Pareto dominance and the constrained dominance principle (CDP) are calculated.Then the next generation of individuals is selected according to the weighted sum sorting,and the process is repeated until the end condition is satisfied to obtain the result sets.Finally,a total of 38 multi-objective optimization problems in three test suites are selected to evaluate the performance of the proposed algorithm,and it is compared with seven algorithms.The simulation results show that COI-AMU_DE has high comprehensive performance in solving constrained multi-objective optimization problems.
Key words:chaotic opposition initialization; multi-objective optimization; differential evolution; mutant operators; average mutation update
0 Introduction
The constraint multi-objective optimization problems (CMOPs) often exist in many engineering applications,such as path planning[1],Web server location[2]and job scheduling[3].CMOPs involve multiple conflicting objective functions and different constraints,which may change the search area and form an infeasible area.Thus,it is more difficult for solving CMOPs[4-5]than unconstrained multi-objective problems.
In recent years,differential evolution (DE)[6]has been increasingly applied to solve multi-objective optimization problems,but it requires optimization among several conflicting objective functions to solve constrained multi-objective optimization problems simultaneously.Thus,how to adjust the trade-off between the objective function and the constraints is crucial.Fan et al.[7]combined the angle information between the solutions and the proportion of feasible solutions to correct the dominance relationship,and further utilized the information of infeasible solutions.Yang et al.[8]designed a multi-objective differential evolution (MODE) algorithm based on the improved constraint method,which could adaptively adjust the parameter values according to the maximum and minimum constraint violations of infeasible individuals.Ozer[9]proposed a chaotic initialization DE algorithm,which had faster convergence speed and better robustness against premature convergence than algorithms using classical random sequence initialization.Wang et al.[10]attempted an adaptive mutation DE algorithm based on particle swarm optimization to solve the slow convergence speed and premature convergence tendency of the original DE.Prabha et al.[11]proposed a mutation strategy based on the biological phenomenon of hemostasis to generate a more promising solution,enhancing diversity through good vectors at early stages,thereby avoiding stagnation at later stages.
DE algorithm often focuses on directly improving the diversity of individuals generated by operators,while less consideration is given to situations where the generation of individuals is illegal,resulting in the concentration of individuals at the boundary and ignoring the distribution of the population.In order to solve multi-objective optimization problems under constraints and balance the diversity and distribution of solutions,a chaotic opposition initialization and average mutation update-based differential evolution(COI-AMU_DE) algorithm is proposed.First,in the initialization process,the tent chaotic map and the opposition-based learning are combined to generate the initial population,the mutation operator is used to generate offspring,and the individual is legalized to return to the decision space.The populations are then ranked for performance according to a weighted sum of Pareto dominance and the constrained dominance principle (CDP),and the weights of the two ranking weighted sums vary dynamically with evolutionary stages.The final selection is based on ranking.
In order to further expand the search direction of individuals,improve the distribution of the initial population and realize efficient search of the solution space,the initial population is generated by using tent chaotic map and opposition-based learning in the initialization process,and all individuals in the population are analyzed according to Pareto advantages and the weighted sum of CDPs is sorted.For individuals who are far from the decision space in the mutation process,a new update operator is designed to legalize it and applied to two mutation operators to further seek the balance among diversity,distribution and convergence.Simulation results on 38 test functions fully demonstrate that COI-AMU_DE has the better or highly competitive performance than other advanced methods.
1 Related work
The ultimate goal of solving a CMOP is to obtain a feasible PF with good diversity and convergence.Therefore,the balance between diversity and convergence is very critical for designing a CMOEA.Yu et al.[12]proposed a dynamic selection preference assisted constrained multi-objective differential evolution (DSPCMDE),which guaranteed diversity and convergence of solutions.The main process of the DSPCMDE algorithm is described as follows.Firstly,Nsolutions are randomly generated in the decision space to form the initial population.Then,during each generation,the mutation and other operations is implemented to produce an offspring population withNsolutionsQt.The dynamic selection preference strategy is applied on the union population to selectNsolutions into the next population.And the above process is repeated until the termination criteria are met.
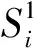
The final ranking is calculated by
(1)
The weightwchanges according tot,and it is calculated by
(2)
Finally,after the individual ranking is calculated,the first better individual with a smaller value is selected to enter the next generation population.
2 COI-AMU_DE
The DE algorithm is a popular evolutionary algorithm for solving complex optimization problems.Furthermore,it exhibits excellent search accuracy,robustness,convergence speed and more ideal low space complexity in challenging optimization problems.The initial population is generated by DSPCMDE using random initialization in the decision space,which cannot be evenly distributed in the decision space.The mutation operation in the algorithm may produce infeasible individuals,and a common patching strategy of modifying directly is according to the maximum and minimum vectors of the decision space.This strategy is simple and straightforward.However,individuals corrected directly in this strategy tend to aggregate on the boundary of the decision space,reducing the distribution of the population,causing individuals to cluster at the boundaries of the decision space,reducing the diversity and distribution of the population.
In order to further improve the quality of PS,two improvements are made to DSPCMDE,and a novel initialization method and mutation update operator is designed.The specific steps of the algorithm are as follows.First,tent chaotic map and opposition-based learning during initialization are used to generate more uniformly distributed random numbers for initial population generation.Then,the mutation update operator is used for the illegal individuals generated by the mutation operator,and the weighted sum of the ranking based on the Pareto dominance and CDP is calculated in each iteration,and the weight changes dynamically with the number of iterations.Finally,the previous individual is selected to enter the next generation according to the ranking of the weighted sum,and the process is repeated until the end condition is met.The approach is called chaotic opposition initialization and average mutation update-based differential evolution (COI-AMU_DE).
2.1 Opposition tent chaotic map
For evolutionary algorithms,the uniform distribution of the initial population in the decision space can improve the solution accuracy and convergence speed of the algorithm,increase the search range of the algorithm,and play a critical role in obtaining the quality of the final solution.In order to obtain a uniformly distributed initial population,the tent chaotic map and opposition-based learning are introduced to generate the initial population.
The tent chaotic map function is
(3)
Tent chaotic map has excellent distribution and randomness.In order to improve the diversity of the population to a greater extent,enhance the global exploration ability of the algorithm and increase the probability of finding the optimal solution,opposition-based learning is introduced to process the mapped population.The opposition-based learning formula is
(4)
where the value ofβis 0.5,andYirepresent theithindividual vector in the population.It can improve the algorithm convergence speed and efficiency,and quickly search for the optimal solution by using tent chaotic map and opposition-based learning.The specific steps for generating the initial population are as follows.First,Nrandom numbers are generated for tent chaotic map generation population.Then,opposition-based learning on the initial population is performed to generate an opposition population of size 2N.As shown in Fig.1,the diversity of the population is improved by opposition-based learning.Finally,Nindividuals selected from the opposition population can be used in the initial population.

Fig.1 Population distribution of opposition tent chaotic map
2.2 Mutation and legalization
Due to the particularity of the problem,the mutated vector individuals may be infeasible because it can not meet the boundary conditions and exceed the range of the solution space.Updating the infeasible solutions is a common operation of evolutionary algorithm[13-14].
A new patch operator is designed to deal with out-of-bounds individuals.Taking DE/rand/2 as an example,the difference vector is generated as
yi=xr1+k[(xr2-xr3)+(xr4-xr5)],
(5)
whereyirepresents the difference vector;r1,r2,r3,r4andr5,are mutually unequal integers;kis the scale factor used to scale the difference vector.
If the difference vectorviexceeds the range of the solution space,then proceed as follows.
First,the average vector is calculated by
(6)
Then,the second mutation is done as
yi,j=xravg,j+k[(xr2,j-xr3,j)+(xr4,j-xr5,j)].
(7)
If the individual is still out of bounds after the second mutation,it is patched as
(8)
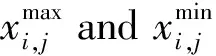
The traditional update method in the mutation process is to update directly according to the upper and lower bounds of the decision space.The update formula is
(9)
Compared with the traditional patching method,the proposed average patching mutation strategy increases the distribution of the population,avoids the dense distribution of the population on the boundary of the decision space and increases the diversity of the population.Fig.1 gives an illustration of the legalization of mutant individuals,in which the solid dots represent the 5 individuals generated by differential,the hollow dots represent the individuals generated by mutation,and the red solid dots represent the average of the 5 individuals.Fig.2(a) illustrates that mutation produces individualp1outside the solution space,and calculates the average vectorxavgof individuals participating in the mutation.xavgfalls among 5 initial individuals,andxavgis subjected to secondary mutation according to Eq.(7) to obtain individualp1,andp2is in the solution space,ensuring the diversity of individuals.In Fig.2(b),the first mutation individualp1exceeds the solution space boundary,and the mentioned secondary mutation is performed on it to obtain that the individualp2is still outside the solution space.At this time,p2is updated according to Eq.(8),andp3is obtained in the solution space,the individual diversity of the decision space is guaranteed.

(a) First patching solution inside the solution space
2.3 Computational time complexity
The COI-AMU_DE algorithm flow is shown in Algorithm 1.The time complexity of the COI-AMU_DE algorithm is mainly determined by the dynamic selection preference strategy and the generation of the offspring population.In the dynamic selection preference,in the worst case,the time complexity of computing Pareto advantage and crowding distance isO(MN2)[15],and the time complexity of CDP and crowding distance is alsoO(MN2),whereMis the target number,Nis the population size.Therefore,the time complexity of the dynamic selection preference policy isO(MN2).In the generation of the descendant population,in the worst case,all generating descendants are infeasible,and the time complexity isO(MN).If it is necessary to use the Pareto advantage on the feasible individuals to select the best individual,the time complexity isO(MN2).To sum up,the overall time complexity of the COI-AMU_DE algorithm isO(MN2),which is the same as most existing MOEAs,e.g.,NSGA-II.
The space complexity of the COI-AMU_DE algorithm is mainly determined by the population size and the calculation of crowding distance matrix.The space complexity of the population isO(ND),and when calculating the crowding distance,the spatial complexity isO(N2),whereDis the dimensional of decision variable.In the improved part,only the reverse population uses additional space,and the space complexity isO(2ND),which is a change in the constant term.Therefore,the overall space complexity of the COI-AMU_DE algorithm isO(N2+ND).
The main process framework of the COI-AMU_DE algorithm is shown in Algorithm 1.

Input:population sizeN,maximum number of iterations MaxGen
Output:populationPt
1t←1

4 Apply a dynamic selection preference strategy with a weight of 0.5 from to select the topNoptimal individuals as the initial population
5Pt+1←∅
6 Whilet≤MaxGendo
7 Generate a descendant populationPtaccording to the populationOt
8 Legalize individuals who are infeasible inOt
9Ht←Pt∪Ot;
10 Apply the dynamic selection preference strategy to selectNoptimal individuals fromHttoPt+1;
11t←t+1
end

3 Simulation
3.1 Simulation setup
A total of three benchmark function sets are used to demonstrate the effectiveness of the COI-AMU_DE algorithm.They are CF[16],LIR-CMOP[7],and MW[17],respectively.CF contains 10 ten-dimensional test functions,LIR-CMOP contains 14 thirty-dimensional test functions,and MW contains 14 fifteen-dimensional test functions.CF has more local optimum regions,the target space in LIR-CMOP has a larger infeasible region,and MW covers various features derived from real-world CMOP.
In order to measure the performance of the multi-objective optimization algorithm more comprehensively,three performance indicators are used in the simulation:feasible rate (FR),inverted generational distance (IGD)[18]and hyper volume (HV)[19].FRis the ratio of the number of runs that CMOEA can obtain at least one feasible solution in the final population to the total number of runs.A larger FR means a higher probability of CMOEA locating a feasible area.Smaller IGD values and larger HV values represent better convergence and diversity performance.
In order to verify the effectiveness of the proposed algorithm,seven kinds of state-of-the-art CMOEAs are selected for system performance comparison.They are HypE-FR[20],NSGA-II-ToR[21],MOEA/D-CDP[22],C-MOEA/D[23],MODE-SaE[24]MOEAD-ACDP[7],and DSPCMDE[12].All simulations are implemented on the platform designed by Tian et al.[24].
The population size on each test function is set to 100.For each test function,each algorithm is independently implemented 30 times to take the mean and standard deviation of the results,and it is stopped when the number of function evaluations reached 60 000.The weightwof the weighted sum is set to 0.5 when the population is initialized for selection.In the simulated binary crossover,the crossover probability and distribution index are set to 1/Dand 20,respectively.In polynomial variation,the variation probability and distribution index are 1/D,and 20,respectively.For the DE operator,the initial value of the shrinkage factorFis 0.5,and the crossover probabilityCRis 1.0.Other parameters in the involved comparison algorithms are set to be the same as in the original article for fair comparisons.
3.2 Results and discussion
In order to better compare the performance of different algorithms,the Wilcoxon signed-rank test is used at the 5% significance level to test the significant difference between COI-AMU_DE and other algorithms.Test results are given in the last row of each table.“+,=,-” indicates that the proposed algorithm performs significantly better/substantially the same/significantly worse than the current algorithm.In the simulation,if an algorithm cannot find a feasible solution on the test function,onlyFRis given.
3.2.1 Comparison results on CF test suite
Tables 1 and 2 give theIGDandHVcomparison results of COI-AMU_DE and other algorithms on the CF test suite,respectively.

Table 1 IGD comparison results of COI-AMU_DE and other seven algorithms on CF test suite (Where “+,=,-” denote that COI-AMU_DE performs betters than,similar to,and worse than other algorithm,respectively)
As shown in Tables 1 and 2,it can be seen that COI-AMU_DE is obviously precede other algorithms on the CF function set by testing each function on the CF data set.Taking CF5 as an example,the values ofIGDandHVindicators are 1.962 5E-1 and 3.456 8E-1 when using the COI-AMU_DE algorithm.Compared with the best algorithms,theIGDis reduced by about 23.8%,and the HV is increased by about 16.1%.
Wilcoxon signed-rank test results showed that COI-AMU_DE performed poorly on CF1 relative to MOEA/D-ACDP.The PF of CF1 is a discrete point,which can be found by MOEA/D-ACDP using the angle information to maintain diversity.COI-AMU_DE is significantly outperformed MOEA/D-ACDP in the remaining 9 functions.
It should be noted that COI-AMU_DE and DSPCMDE can obtain 100%FRon all tested functions,while other algorithms cannot obtainFRon CF8 and CF10 due to their feasible PF being disconnected and hindered by the large infeasible region in each run.
3.2.2 Comparison results on LIR-CMOP test suite
Tables 3 and 4 give the comparison results ofIGDandHVon the LIR-CMOP test suite set of COI-AMU_DE and other seven algorithms,respectively.

Table 3 IGD comparison results of COI-AMU_DE and other seven algorithms on theLIR-CMOP test suite (Where “+,=,-” denote that COI-AMU_DE performs betters than,similar to,and worse than other algorithm,respectively)
As shown in Tables 3 and 4,it is obviously better than other algorithms by using COI-AMU_DE on the LIR-CMOP function set by testing each function on the LIR-CMOP data set.Taking LIR-CMOP5 as an example,when using the COI-AMU_DE algorithm,the values ofIGDandHVindicators are 2.709 1E-1 and 4.494 6E-1,respectively.Compared with the best algorithms in others,IGDis reduced by about 36.8%,andHVis increased by about 13.3%.It is worth noting that some of theHVvalues in Table 4 are 0,because the solutions found by the corresponding algorithms are all dominated by reference points.
Wilcoxon signed-rank test results show that COI-AMU_DE is significantly superior to NSGA-II-ToR,MOEA/D-CDP,C-MOEA/D,MOEA/D-ACDP and HypE-FR on all test functions.MODESaE is significantly superior to COI-AMU_DE on LIR-CMOP1-4,while the remaining 10 test functions are significantly worse than COI-AMU_DE.DSPCMDE is significantly worse than COI-AMU_DE in most test functions,and it only has basically the same performance as COI-AMU_DE in a few test functions.

Table 4 HV comparison results of COI-AMU_DE and other seven algorithms on the LIR-CMOP test suite (Where “+,=,-” denote that COI-AMU_DE performs betters than,similar to,and worse than the other algorithm,respectively)
In summary,COI-AMU_DE obtains the best performing on the LIR-CMOP test suite.MODESaE has a certain competitiveness.It adaptively adjusts theεlevel according to the maximum and minimum constraint violation values of infeasible individuals and switches the global search and local search through adaptive parameters.Thus,the algorithm is suitable for CMOPs with low feasibility in the search space.The advantage of DSPCMDE in LIR-CMOP13-14 test functions is due to the utilization of information in the objective function.
3.2.3 Comparison results on MW test suite
The comparison results ofIGDandHVon the MW test suite for COI-AMU_DE and other seven algorithms are presented in Tables 5 and 6,respectively.It can be seen that COI-AMU_DE is obviously better than other algorithms on the MW function set by testing each function on the MW data set.Taking MW6 as an example,the values ofIGDandHVindicators are 1.968 5E-1 and 3.034 5E-1,respectively,when using COI-AMU_DE algorithm.Compared with the best algorithms,theIGDis reduced by about 33.0%,and theHVis increased by about 29.1%.
According to the Wilcoxon signed-rank test results,COI-AMU_DE is significantly superior to other algorithms in 10,11,11,10,10,13,and 10 test functions in theIGDcomparison results,respectively.And COI-AMU_DE is significantly superior to other algorithms at 10,11,10,10,10,13,and 8 test functions in theHVcomparison results.
In terms ofFRresults,most algorithms cannot achieve 100%FRon all test functions.Only COI-AMU_DE and DSPCMDE can consistently find feasible solutions for each test function in 30 independent runs.There are 10 test functions that are significantly better than DSPCMDE,and 8 test functions are significantly better than DSPCMDE in theHVcomparison results.

Table 5 IGD comparison results of COI-AMU_DE and other seven algorithms on the MW test suite (Where “+,=,-” denote that COI-AMU_DE performs betters than,similar to,and worse than other algorithm,respectively)

Table 6 HV comparison results of COI-AMU_DE and other seven algorithms on the MW test suite (Where “+,=,-” denote that COI-AMU_DE performs betters than,similar to,and worse than other algorithm,respectively)
3.2.4 Ablation simulation
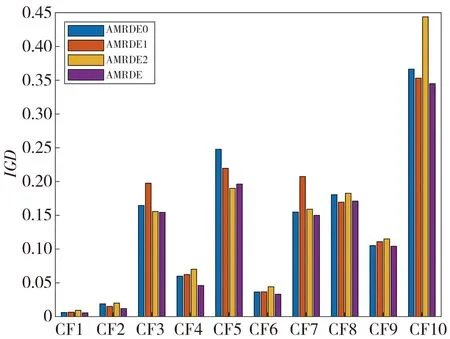
The COI-AMU_DE algorithm is compared with other algorithms by simulations,and the superiority of the COI-AMU_DE algorithm compared with other algorithms is confirmed.In order to further explore the effectiveness of the improved strategy on the COI-AMU_DE algorithm and the impact of the improved strategy on the performance,the comparison results of algorithms with different improvement strategies are presented.COIAMUDE0 contains the average mutation update strategy,COIAMUDE1 includes the opposition chaotic map,and COIAMUDE2 does not include the improvement strategy.The abscissa of the comparison result graphs represents the test function number,and the ordinate represents the average value of theIGDorHVindex of 30 running results.It is shown in Fig.3.
(a) IGD comparison results of different algorithms on CF test suite
COIAMUDE2 without an improved strategy performs the worst on the three test function sets.COIAMUDE0 and COIAMUDE1 perform better,outperform COIAMUDE2 on most test functions,and COIAMUDE performs the best overall.For example,the IGD values of COIAMUDE,COIAMUDE0,COIAMUDE1,and COIAMUDE2 obtained by running on the test function CF1 are 0.005 6,0.006 1,0.006 6,and 0.009 3,respectively,and the IGD values obtained by running on the test function CF1 are 0.012 0,0.018 9,0.015 1,and 0.019 9,respectively.It is because the COIAMUDE0 initialized by the opposition chaotic map only increases the distribution of the initial population and accelerates the convergence of the population,while the population diversity cannot be guaranteed during the iteration process.COIAMUDE1 with hybrid opposition chaotic map updates the infeasible solution in the iterative process,which increases the diversity of the population and reduces the density of the boundary of the decision space,but the distribution of the initial population is insufficient,resulting in insufficient convergence.COIAMUDE not only improves the initial population distribution,but also enhances the diversity in the population iteration process,so as to obtain the optimal effect.
4 Conclusions
In order to further expand the search direction of individuals,increase the diversity of the population and avoid individuals from gathering at the boundary during the mutation process,a differential evolution algorithm with a hybrid opposition chaotic map and an average update mutation strategy,i.e.,COI-AMU_DE,is proposed.In this algorithm,tent chaotic map and opposition are performed on random numbers in the initialization process to generate more uniformly distributed random numbers for generating the initial population.Then the individuals generated by the mutation are legalized,and the weighted sum of the ranking based on Pareto advantage and CDP is calculated in each iteration,and the weight changes dynamically with the number of iterations.Finally,the firstNindividuals are selected to enter the next generation according to the weighting and sorting,and the above process is repeated until the end conditions are met.To verify the effectiveness of COI-AMU_DE,a total of 38 multi-objective optimization problems in three test suites are selected and compared with other algorithms.The simulation results show that COI-AMU_DE has strong competitiveness in solving constrained multi-objective optimization problems.
Nevertheless,there is still a difficult problem to set the parameters existing in algorithm,which has a great impact on the simulation results.Therefore,in the further research,more attention should be paid on the parameter setting strategy to improve the feasibility of the algorithm.
 Journal of Measurement Science and Instrumentation2023年4期
Journal of Measurement Science and Instrumentation2023年4期
- Journal of Measurement Science and Instrumentation的其它文章
- A synchronous scanning measurement method for resistive sensor arrays based on Hilbert-Huang transform
- A covert communication method based on imitating bird calls
- Remote sensing images change detection based on PCA information entropy feature fusion
- An image dehazing method combining adaptive dual transmissions and scene depth variation
- Research on restraint of human arm tremor by ball-type dynamic vibration absorber
- Drive structure and path tracking strategy of omnidirectional AGV
