基于挠度及应变影响线差值曲率的连续箱梁桥损伤识别方法
孙文卓,石英迪
(安徽建筑大学土木工程学院,安徽 合肥 230601)
桥梁作为载人、承物的重要结构,在人们的生产生活中发挥着重要作用。桥梁在使用过程中受到不同因素的影响,会产生裂缝、剥蚀等现象,造成结构损伤。当前国内外常用的桥梁检测方法主要是局部检测法和整体检测法。局部检测法具有目标针对性强、检测结果准确等优点,但是在应用前需要了解损伤的大致位置,以确保检测仪器能够准确识别损伤区域[1-3]。整体检测法是指通过损伤前后结构参数(位移、应变、振型等)的变化诊断结构损伤的方法,大致可以分为动力指纹法、BP神经网络法、遗传算法、小波分析法等[4-6]。整体检测法具有评价桥梁整体承载能力和损伤位置的优点,但是往往只能大致确定损伤位置,需要结合局部检测法进一步提供损伤信息。
作为桥梁的固有特征,影响线具有物理意义明确、对损伤敏感、对环境变化影响不明显等特点,它包含了丰富的桥梁局部信息[7]。因此,国内外众多学者基于影响线开展了多种损伤识别研究。周宇等[8]通过推导弹性约束梁应变影响线的解析表达式,揭示了弹性约束刚度和局部损伤参数与主梁任意截面应变影响线的关系,为非理想支承下的梁式子结构力学分析提供了理论依据。陈志为等[9]通过推导两跨连续梁支座反力影响线损伤前后的函数表达式,揭示了反力影响线适合于构造连续梁桥损伤指标的原因。刘纲等[10]通过理论推导,说明了损伤力影响线方法识别静定桥梁结构损伤部位和损伤程度的方法,并根据该方法的特点将其推广到静定梁结构多处损伤的识别。李东平等[11]提出一种基于实际影响线的桥梁快速检测方法,采用单一车辆标定试验代替多车辆静载试验,解决了静载试验开展成本高、耗时长和需要阻断交通等问题,有效提高了桥梁检测速率。这些研究大多采用动态指标进行损伤识别,例如频率、振型、柔度等,测得的数据易受外部环境影响从而产生较大误差,而且测试时需布置较多传感器,难以在实际应用中实施。静态指标(如挠度影响线、应变影响线)与动态指标相比,只需布置少量传感器就可测得数据,具有易实施、误差小、精度高的优点。
因此,本文采用静态指标,提出了一种基于挠度及应变影响线差值曲率的损伤识别方法。通过建立三跨等截面连续箱梁桥有限元模型,进行了数值模拟,验证了方法的可行性与抗噪性能。
1 理论分析
挠度影响线(Deflection Influence Line,DIL)为梁上某一位置处的挠度随着集中荷载的移动而发生变化的规律曲线;应变影响线(Strain Influence Line,SIL)为梁上某一位置处的应变随着集中荷载的移动而发生变化的规律曲线。若梁上出现损伤,则损伤位置的曲率必定会发生变化[12-13]。假设集中荷载F作用在全长为L的连续梁上,D点位置存在损伤,损伤范围为(d+ε,d-ε),C点为测点位置,具体布置见图1。

图1 荷载及损伤位置
因此,当集中荷载处于无损范围内时,R=0,当集中荷载处于有损范围内时,
式中:EI为无损范围内的抗弯刚度;EI′为有损范围内的抗弯刚度;F为集中荷载;λ为点A距测点位置C的距离;L为连续梁长度;xf为点A距集中荷载的距离。
2 有限元数值模拟
本文采用MIDAS/Civil软件建立等截面连续箱梁桥的有限元模型。通过数值模拟的方法来验证在不同损伤工况下,挠度及应变影响线差值曲率的识别效果。桥梁模型全长为70 m,桥跨布置为20 m+30 m+20 m。将全桥划分为81个节点、79个单元,桥梁纵向共设置71个加载步,每1 m为一个间隔。桥面板采用C50混凝土,E=3.45×104N/mm2。桥梁有限元模型见图2。对模拟结果进行分析,得出单点损伤和多点损伤情况下挠度差值曲率及应变差值曲率曲线图(见图3~图9)。

图2 桥梁有限元模型

图3 DILDC曲线(工况1)
2.1 DILDC损伤工况设置及结果
为验证挠度影响线差值曲率(Deflection Influence Line Difference Curvature,DILDC)对单点损伤情况识别的有效性,现设置以下工况:工况1中损伤位于#35单元,测点位置布置在#17单元;工况2中损伤位于#17单元,测点位置布置在#35单元。本文通过降低关键截面单元材料的弹性模量模拟损伤程度[14],如表1所示。

表1 挠度单点损伤工况
由图3、图4可知,DILDC在损伤位置#35、#17单元处产生突变,其突变峰值随损伤程度的变化而变化,当损伤程度为90%时,突变峰值达到最大。由此可得,在单点损伤工况下,可以根据DILDC是否发生突变识别损伤位置。

图4 DILDC曲线(工况2)
为验证DILDC对多点损伤情况识别的有效性,设置以下工况:工况3中的损伤位于#17、#54单元,测点位置布置在#17单元;工况4中的损伤位于#17、#54单元,测点位置布置在#35单元。具体工况见表2。

表2 挠度多点损伤工况
由图5、图6可知,DILDC在损伤位置#17、#54单元处产生突变,且损伤处的突变峰值均在损伤程度为90%时最大。由此可得,在多点损伤工况下,也可以根据DILDC是否发生突变识别损伤位置。

图5 DILDC曲线(工况3)
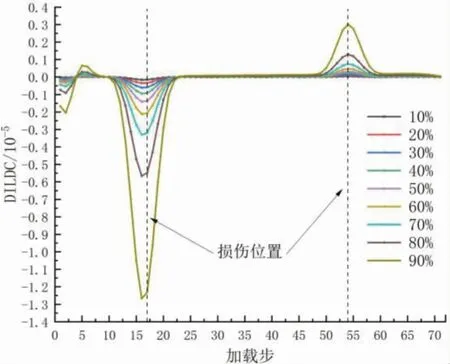
图6 DILDC曲线(工况4)
2.2 SILDC损伤工况设置及结果
为验证应变影响线差值曲率(Strain Influence Line Difference Curvature,SILDC)对单点损伤情况识别的有效性,现设置以下工况:工况5中的损伤位于#17单元,测点位置布置在#17单元;工况6中的损伤位于#35单元,测点位置布置在#35单元。具体工况见表3。

表3 应变单点损伤工况
由图7、图8可知,SILDC在损伤位置#17、#35单元处产生明显突变,通过对比40%、50%、60%损伤程度下的曲率突变峰值,可以明显看出同一损伤位置处的曲率峰值会随着损伤程度的变化而变化。由此可得,在单点损伤工况下,可以通过SILDC是否发生突变来识别损伤位置,并且可以根据损伤位置处的SILDC突变峰值来判断损伤的严重程度。

图7 SILDC曲线(工况5)
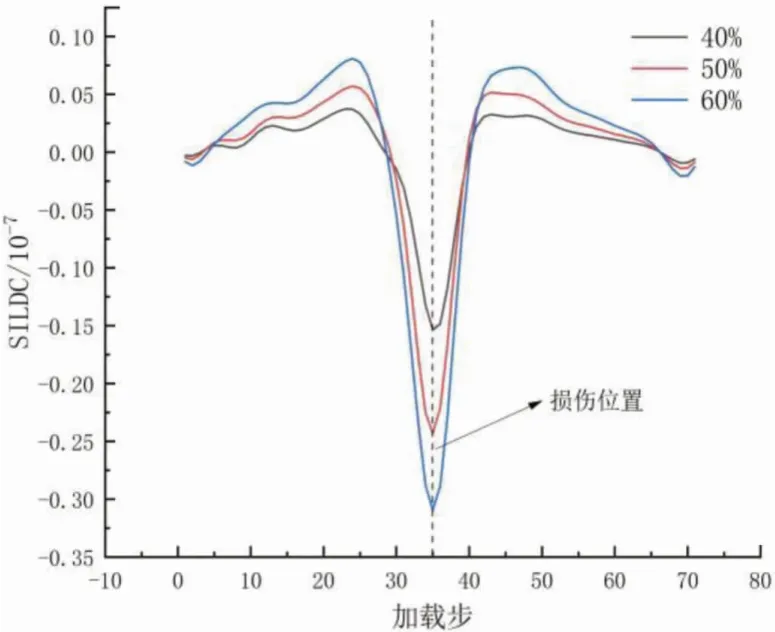
图8 SILDC曲线(工况6)
设置以下工况验证SILDC对多点损伤情况识别的有效性。工况7中的损伤位于#17、#54单元,测点位置布置在#35单元。具体工况见表4。

表4 挠度多点损伤工况
由图9可知,SILDC在损伤位置#17、#54单元处仍会产生明显突变,通过对比40%、50%、60%损伤程度下的曲率突变峰值,可以看出同一损伤位置处的曲率峰值同样会随着损伤程度的变化而变化。由此可得,在多点损伤工况下,仍可根据SILDC是否发生突变及突变峰值来识别损伤位置并判断损伤的严重程度。

图9 SILDC曲线(工况7)
2.3 损伤程度拟合
为验证DILDC能否准确判断损伤的严重程度,现对不同损伤程度下的曲率突变峰值进行拟合。结果见图10~图13。
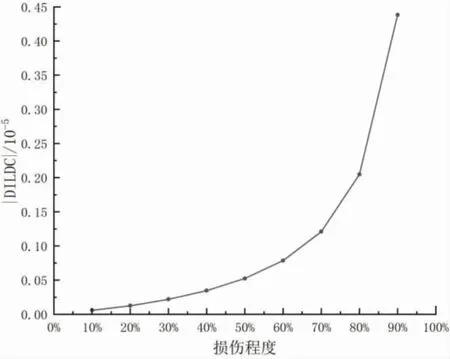
图10 突变峰值细部(工况1)
在图10、图11中,通过对比10%、20%、30%、40%、50%、60%、70%、80%、90%损伤程度下的曲率突变峰值可知,同一损伤位置处的曲率峰值会随着损伤程度的增大而逐步增大。因此,在单点损伤工况下,可以根据损伤位置处的DILDC突变峰值来判断损伤的严重程度。

图11 突变峰值细部(工况2)
在图12、图13中,通过对比10%、20%、30%、40%、50%、60%、70%、80%、90%损伤程度下的曲率突变情况可知,同一损伤位置处的曲率会随着损伤程度的增大而逐步增大。因此,在多点损伤工况下,也可以根据损伤位置处的DILDC峰值来判断损伤的严重程度。

图13 突变峰值细部(工况4)
3 抗噪性能研究
本文运用有限元数值模拟的方法对三跨等截面连续箱梁桥进行损伤识别研究,但在实际测量中,由于受到外部环境激励等因素的影响,导致识别结果存在误差。数值模拟是在理想状态下对结构进行研究,无法模拟出真实环境中的各种误差。因此为验证抗噪性能,本文引入噪声误差分析。在实测环境下,风速、车辆行驶震动等因素均可造成影响线指标具有噪声,且噪声具有不确定性,故随机选取噪声程度为5%、9%、13%的高斯白噪声模拟测量过程中出现的误差。随机选取方式可模拟出真实环境中噪声随机的情况,且由于工程实践中噪声影响一般不超过10%,选取13%的噪声强度可验证该指标的稳定性,能够说明该指标在实际工程中具有较强的可行性,以工况1和工况6中50%的损伤程度为例。引入噪声后的挠度和应变的计算公式为
式中:ωn是理想状态下的挠度和应变;η是噪声强度水平;ξ是[-1,1]范围内的随机数。
具体识别结果如图14、图15所示。由图14、图15可知,引入噪声后,DILDC及SILDC仍能有效识别出损伤位置。在引入5%的噪声后,DILDC突变峰值较无噪声时略有增长;当引入9%、13%的噪声时,DILDC突变峰值较无噪声时略有减少;在引入3种噪声后,无损位置处均会出现波动。对SILDC而言,在引入5%、9%、13%的噪声后,其突变峰值与噪声强度水平呈负相关,在无损位置处也会出现波动。因此,有损位置的损伤识别效果会受外部环境激励等因素的影响,但DILDC及SILDC损伤指标具有抗噪性,仍能有效识别损伤位置。

图14 DILDC损伤识别结果(工况1)

图15 SILDC损伤识别结果(工况6)
4 结论
采用静态损伤指标,提出了一种基于DILDC和SILDC相互验证的连续箱梁桥损伤识别方法。该方法在已有DIL损伤识别方法的研究基础上,考虑SIL同样包含大量的桥梁结构信息,将DILDC和SILDC作为损伤指标,两损伤指标相互验证且相互补充,对识别结果进行分析,在多种损伤工况下,DILDC和SILDC损伤指标均可有效地对连续箱梁桥的损伤进行定位定量。由于DIL数据和SIL数据在实际工程中容易获得,识别方法简便、识别效果良好,故在实际工程中对桥梁结构健康监测的实施具有重要意义。通过构建三跨等截面连续箱梁桥有限元模型,结合7种工况的分析结果,得到了以下结论:
(1)在单点及多点损伤工况下,根据DILDC是否发生突变可以有效识别等截面连续箱梁桥的损伤位置,并且可以根据损伤处的突变峰值,来判断损伤的严重程度。SILDC与DILDC相同,均可有效识别等截面连续箱梁的损伤位置并判断损伤的严重程度。
(2)DILDC损伤指标曲线峰值随着损伤程度的增大而增大,呈线性变化,故DILDC损伤指标具有良好的识别效果。
(3)通过抗噪性能研究发现,外部环境激励等因素产生的噪声会使影响线在无损位置处产生波动,但并不会影响DILDC及SILDC对损伤位置的识别,随着噪声强度的增大,损伤位置处识别出的突变程度相较于无噪声时的突变程度降低。

