多普勒与航向姿态坐标参考的组合导航系统设计
冯爱国,吴 炜
(1. 江苏航运职业技术学院 航海技术学院, 江苏 南通 226010;2. 江苏航运职业技术学院 交通工程学院, 江苏 南通 226010)
0 引言
在船舶航行过程中,导航与定位非常重要。导航方式主要有两种,一种是基于外部信号的非自主导航,如罗兰、欧米加、GPS、北斗系统等无线电定位和主要应用于水下定位的基于声学信标的声学定位导航[1],对于水面船舶,基于无线电的非自主导航方式,如罗兰、欧米加、GPS、北斗等,由于电磁波传播等条件限制,在使用中存在较大的不稳定性;另一种是基于传感器的自主导航,主要依靠船舶航向、航速传感器如陀螺罗经、计程仪等手段完成推算式导航,近年来随着惯性技术(IMU)、声学导航、地形匹配、地磁传感器、地球物理传感器等技术发展,给自主导航技术的发展提供了很大的空间[2]。因此,将多种导航技术适当地组合,可以取长补短,降低对单一导航系统的依赖程度,提高系统的可靠性和容错性[3]。
1 系统设计方案与总体结构
系统由双轴多普勒计程仪、陀螺罗经、微机械型捷联惯导组成。微机械型捷联惯导由呈三轴正交布置的三个微加速度计和三个微硅陀螺组成,其他部分由船用GPS 接收机或北斗电子定位模组、低通滤波器、A/D转换电路、计算机组成。系统总体结构关系如图1 所示。

图1 多普勒与航向姿态融合的组合导航系统
1.1 传统自主式船位推算
船位推算法是无线电定位之外最常用的且应用最早的导航方法,其基本思想是将载体的速度对时间进行积分来获得载体的位置。这种方法需要利用风、流信息和航向传感器在航速、航向,然后推算出船舶位置[4]。风、流的信息会给载体产生速度的分量,而分量无法通过传感器实时测量,仅利用其他预报获得的先验数据,尤其在低速且长时间航行情况下,将产生很大的定位误差。
考虑风、流影响的推算,采用“先风后流”的作图方法,即先考虑风的影响,求取风中航迹线,再在风中航迹线上作水流三角形,求取推算航迹向和推算船位,流程如下:①自起始点A 绘画真航向线;②自A 点绘画风中航迹线;③在风中航迹线上截取一点D,使AD=SL,SL为计程仪航程;④自A 点画水流矢量AB,AB 长等于流程SC,过B 点作AD 平行线,以AD 长度截得C 点,C 即为推算船位;联结A、C 为推算航迹线。
具体方法如图2 所示,图中,α 为风压差角,指风使船舶向下风漂移,其航迹线与真航向线之间的夹角;β 为流压差角,船舶在水流影响下,会在水流的作用下顺水漂移,流中航迹线与风影响后的航迹之间的夹角;γ 为风流合压差,真航向与风流影响下的航迹向之间的交角称为风流合压差角。风流合压差γ 等于风压差α和流压差β 的代数和,即:γ=α+β。
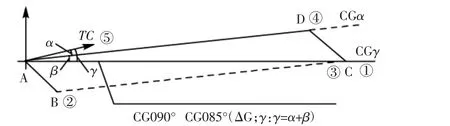
图2 风、流影响下的船位推算
由推算流程可知,该方法适用于对水航速基础上进行推算。有风流情况下,航迹推算的精度除了与航迹推算中的航向误差和航程误差有关外,主要还取决于估算风压差和水流要素的误差。综合各项因素的标准差,可以得到有风流情况下推算船位误差圆半径为推算航程的5%~8%。
1.2 多普勒结合航向姿态参考的自主式船位推算
对于使用多普勒计程仪(Doppler velocity log,简称“DVL”)的船舶,大多数情况下可以测量跟踪海底的对地速度,从而可以消除海流对船舶定位的影响,达到较高的定位精度。目前高精度DVL,如美国EDO 公司的3040 型和3050 型DVL,其精度可达0.2%;美国RD Instruments 的Workhorse Navigator 系列和SonTek 的ADP 声学多普勒剖面仪,其精度也可达0.2%;英国MA 研制的COVELIA,其最大绝对误差不大于0.005 kn。目前,一般商船配备的多普勒计程仪性能标准要求测速精度不大于0.01 kn。[5]47严卫生等也给出了在关键领域不依赖外来信号而进行自主导航的技术方案。[6]
多普勒计程仪依据多普勒频移原理进行速度测量,在船底安装收发公用换能器,船向前以速度V相对于海底航行。换能器的一个笔形波束以俯角α 向下发射声波,接收到的回波信号频率为:
将式(1)按泰勒级数展开,舍去高次项,可得:
其中,fd为多普勒频偏;V为船速;f0为发射频率;c为超声波在海水中的传播速度;α 为俯射角。f0、c、α 均为已知量,fd为测量值,由式(2)可得到船速V。
实际的船用多普勒计程仪因摇摆、偏荡运动带来很大误差,常采用詹纳斯配置,纵、横向各成对对称发射,构成了四波束詹纳斯配置。采用詹纳斯配置的多普勒计程仪分别测出两个速度Vx和Vy,为与后文相统一,设船舶为运动载体,纵、横运动速度,多普勒系统测量得到载体坐标系的速度为Vx和Vy。
由于船舶位置解算的是在导航坐标系下进行的,因此必须把所测出的速度转换到SINS 的导航坐标系统中,经数学处理(如忽略高阶小量)后,得DVL 输出的数学表达式。四波束多普勒可直接测得对地速度在载体坐标系上的分量。利用载体航向姿态角,可直接向地理坐标系投影,而不需要额外配置风流压角。
陀螺罗经测量的航向GC=TC+φU,TC为真航向,φU为航向误差,捷联惯导中又称方位失准角。角度的正负按照航海习惯确定,以真北方向为基准,顺时针为正,如图3 所示。

图3 多普勒测速各坐标系的关系
图3 中的三个坐标系n、n′、b分别为地理坐标系、计算(测量)地理坐标系、载体坐标系。多普勒测速误差(δVdx,δVdy),刻度系数误差(δKx,δVdy),得:
多普勒计程仪DVL 所测的速度在地理坐标系投影,得:
式(4)中,令多普勒测速误差和刻度系数误差为零,罗经差φU已知,可得东、北向速度
而其余部分即为多普勒测速误差:
式(5)+式(6)可得地理坐标系下多普勒计程仪的速度为:
以地理坐标系下东、北向速度为基础进行航迹推算,式中Re为近似地球半径,φk+1、λk+1为计算周期给出的定位结果。
2 系统误差分析与补偿
多普勒测速仪DVL 误差包含多普勒测量误差、刻度误差及噪声,误差方程可以表示为:
式中,τdx、τdy为DVL 测量误差相关时间常数;wdx、wdy为激励马尔可夫过程的白噪声。
多普勒测速系统的状态变量为:
状态方程为:
四波束多普勒测速仪测得船舶载体坐标系的对地速度分量,变换到地理坐标系,然后与捷联惯导的相应输出信息相减,得到SINS/DVL 形成的速度量测量。
设捷联惯导速度输出为:
假设与多普勒测量相关的捷联惯导状态变量XSINS已知,SINS/DVL 形成的速度量测量为:
基于DVL 状态方程,运用卡尔曼滤波算法,获得δVdx、δVdy、δKx、δKy,代入式(6)。基本方法为:当量测值不断增大时,动态调整状态变量,期望按滤波方程计算的估计均方误差趋于零或趋于某一稳态值,从而获得最佳状态变量,即获得多普勒测量误差及刻度误差XDVL=[δVdxδVdyδKxδKy]T及噪声的最优估计,而利用计算机可以得到动态系统中具有一定随机性的多普勒测量状态变量的高精度、实时的最优估计[7]。而假设φU也不确定,可将式(7)扩展为更多维度的组合系统的状态变量,可根据捷联惯导罗经法对准原理进行失准角迭代计算[8]。
3 系统仿真分析
为验证所建立的组合导航系统的数学模型及性能,进行软件仿真分析。考虑到船舶运用中受风流、浪涌、风偏以及其他不可预测性因素的影响,船舶运动航向与姿态角变化复杂,致使系统输出存在误差。因此根据船舶运动特点对组合导航模型进行软件仿真,验证其有效性。
3.1 仿真条件及参数
船舶运动方式:曲线机动运动,仿真时间为6 小时,在t=0~1 000 s,航向以1.8°/s 的角速度匀速转向;在t=1 000~3 000 s 做匀速直线运动。
初始姿态角:纵摇角为0°,横摇角为0°,航向角为45°。
初始速度:8 m/s,北向速度5 m/s。
船舶摇摆方式:纵摇角幅值为9°,周期为8 s;横摇角幅值为10°,周期为10 s。
陀螺罗经初始误差:φU(0)=0.15°。
SINS 初始姿态角误差:φE(0)=φN(0)=φU(0)=0.15°。
DVL 误差:测速误差为0.4 m/s,系数误差为0.000 1。
3.2 仿真分析
图4、图5 是以假设定位误差可忽略条件下的电子定位系统DGPS 为参考的组合导航系统在kalman 滤波模型下的速度、位置误差随时间变化的曲线。

图4 速度误差曲线

图5 位置误差曲线
仿真结果表明,在传统航迹推算或同等的航迹计算中,由于先验风、流信息的不确定性以及船舶的机动运动(加减速运动、转向和摇摆运动)的影响,风致航迹与流致航迹均不可靠,且速度误差波动很大,导致位置误差随时间累积增大很快,在现代船舶驾驶台中作为主要船位来源的验证与备用手段,其有效性很差。而本方案的仿真结果显示,本文采用詹纳斯配置多普勒测速结合航向姿态进行船位推算,结合卡尔曼滤波算法,能保持良好的滤波精度及误差纠正能力。
4 结束语
本文是源于现代船舶导航需求而进行研究。因为随着船舶对导航精度要求的不断提高,单一的导航方式已经无法满足实际要求。鉴于船舶在海上航行风流影响大、自身航向姿态变化复杂等特点,在无线电定位等非自主式导航之外,利用自身航速、航向、姿态等信息进行精确导航具有重要意义。但是传统的航迹推算在复杂航行条件下应用具有很大的局限性,长时间远距离的推算使导航精度难以保证。本系统采用GYRO/DVL/SINS/EPFS 组合导航,以陀螺罗经结合SINS 航向罗经法对准技术,可以将动态航向误差控制得很低,信息融合采用自适应Kalman 滤波算法,提高了改进后的航迹推算组合导航系统信息匹配的可观测度。仿真结果表明,本文所设计的组合导航系统能够有效提供高精度的导航信息。

