高能X射线光谱分析工具—SasalPy

郝明月,梁贵云,王 凯,毛俊捷

(1.河北大学,保定 071002; 2.中国科学院国家天文台,北京 100101; 3.清华大学,北京 100084)

1 引 言

高能X射线研究是天文学家探究高能天体物理过程的主要研究手段，常见的X射线辐射源如太阳或者恒星的星冕和耀斑、超新星遗迹、激变变星、X射线双星和黑洞周围的吸积盘、星系、活跃星系核、星系团等.随着现代天文的蓬勃发展，尤其是XMM-Newton、Chandra和Hitomi等天文望远镜的观测为天文学家研究高能X射线、探究和认知宇宙高能物理过程提供了重要的观测数据.

建立在各种物理条件下的等离子体模型是天文学家解析反演上述天文望远镜观测到的数据的重要工具，是现代天文学研究工作的基础.目前，被广大天文学家熟知的等离子体模型有CHIANTI[1]、APEC[2]、Raymond-Smith[3]、MEKAL[4]、SPEX[5]、XSTAR[6]、Cloudy[7].其中，由Landi等[8]人提出的CHIANTI主要关注的研究对象是太阳的极紫外辐射光谱；由Smith等[2]人提出的APEC[2]最早用于计算辐射率和冷却曲线，是当前美日学者分析X射线能谱数据的首选方法；由Raymond[3]提出的Raymond-Smith等离子体模型适用于星际介质；由Mewe等[4]人提出的MEKAL是高能X射线研究早期被广泛应用的等离子模型；目前为天文学家广知的XSPEC[9]、SPEX[5]都包涵MEKAL的基本模型，XSPEC是由Arnaud等[9]提出的光谱拟合工具，它除了包含MEKAL模型外，同时还集成了APEC[2]和XSTAR[6]模型，由Kallman和McCray提出的XSTAR主要用于研究由光电离等离子体产生的X射线能谱；SPEX是由Kaastra等人[5]提出的光谱拟合工具包，它包含的碰撞电离平衡模型延续了Mewe等人[4]的工作，同时它还包含非电离平衡模型和有限的光电离平衡模型；对于光电离等离子体来讲，由Ferland等人[7]提出的Cloudy模型也被天文学家应用，近期该模型也向X射线波段扩展.

本工作中描述了一种全新的等离子体光谱分析模型，即SasalPy，它是为了满足新一代X射线望远镜海量数据和极高能谱分辨需求提出的新的等离子体光谱分析工具，该模型主要是基于Python语言并在SASAL[10](Spectral Analysis Sys-tem for Astrophysical and Laboratory)模型的IDL版本基础上发展的新的X射线光谱分析工具包，以激发/退激发、复合、电离三类原子物理过程为基础构建热碰撞电离平衡(Collisional Ionisation Equilibrium，简称CIE)模型.对于热等离子体来讲，其微观物理过程构成具体包含电子和质子的激发和退激发、光子激发和受激辐射、辐射复合和双电子复合、三体复合和碰撞电离等原子物理过程，热等离子体广泛存在于恒星星冕、星系、星系团、超新星遗迹等天体中.SASALDB是SasalPy数据交互的基础数据库，涵盖所有天体高丰度元素，即从氢(Z=1)到锌(Z=30)30号元素的相关原子参数.SASALDB数据库的持续更新和发展有助于等离子体模型SasalPy精确性提升.SasalPy仍在开发当中，下文主要从SasalPy当前已经完成的碰撞电离平衡模型的理论、主要框架和功能展开介绍.第二部分简要介绍SasalPy的碰撞电离平衡模型的理论基础，第三部分主要介绍碰撞电离平衡的总体框架和主要功能以及与其他等离子体模型的对比研究，第四部分是对SasalPy的碰撞电离平衡模型研究的结果与讨论.

2 碰撞电离平衡模型

假设等离子体光学薄并且无外部辐射场的影响，碰撞电离平衡状态下等离子体的电离过程和复合过程处于动态平衡状态，即由复合捕获的自由电子数等于由电离产生的自由电子数.该状态下主导的电离过程为直接碰撞电离和激发自电离，主导的复合过程为辐射复合和双电子复合.当等离子体处于低温时，电荷交换过程的影响不可以被忽略.电荷交换过程不在本文研究范围，后续的研究中会加入到模型中.

2.1 电离平衡

电离平衡主要是描述不同电荷态离子相对于离子对应元素总量在一定温度和一定密度下的相对含量，或者称其为电荷态分布.电离平衡过程可用梁贵云等[10]工作中第二部分(1)-(6)式描述的速率方程表述，通过求解方程即可得到特定温度和密度条件下该电荷态的分布情况.不考虑光致电离过程与电荷交换过程的速率方程可表述为：

(1)

(2)

(3)

(4)

2.2 线辐射

线辐射对于热等离子体来说起着至关重要的作用.在特定情况下，线辐射在总的辐射量中占据主导地位.由碰撞激发产生的线辐射可以分为离子外层电子的激发和辐射衰变两个阶段，而由复合过程引起的线辐射是在电子与离子发生复合后接续发生辐射衰变产生的.在发生辐射之前，离子需要先通过碰撞激发、吸收光子、内壳层电子电离以及辐射复合或双电子复合过程达到激发态，随后处于激发态的离子通过辐射回到基态或者亚稳态，产生线辐射.假设原子或离子先激发至激发态j，随后经过辐射跃迁回到基态或能量较低的能级i，单位时间处于能级j的电子由于自发辐射跃迁至较低能级i的速率为Aji(单位：s-1)，对于不同能级的辐射跃迁，辐射跃迁速率不同.线辐射率可以表述为：

εji=ΔEnjAji

(5)

ΔE是激发能量，即能级i与能级j之间的能级能量差，nj是经过归一化的处于能级j的相对离子数密度，即nj=Nj/∑Nk，Nj是能级j的能级布居，∑Nk表示所有求解目标能级的布居总和.

2.3 连续辐射

连续辐射主要包括轫致辐射、复合辐射和双光子辐射.轫致辐射可以概述为等离子体中的自由电子在离子的库伦场作用下做加速运动产生的辐射.Nozawa等[11]工作中(23)式很好的描述了相对论条件下的轫致辐射，本文(6)式在此式基础上应用了Itoh等[12]计算的相对论条件下的冈特因子：

(6)

(7)

(8)

其中，h是普朗克常数，c是光速，k是玻尔兹曼常数，λ是辐射光子对应的波长，Ael是离子对应的元素丰度，FZj是离子对应温度T下的电荷态分布数据，Zj为原子序数，此处j特指对应的离子，即离子电荷量加1，gzj，itoh为冈特因子，me为电子质量.本文(9)式描述的是采用了Sutherland等[13]计算的冈特因子的轫致辐射：

(9)

(10)

由Itoh等[12]计算的相对论冈特因子适用的温度范围为106K≤T≤108.5K，适用的波长范围为14.39 Å≤λ≤4549.81 Å.本文中对于超出以上温度和波长范围的辐射采用由Sutherland计算[13]的冈特因子.

复合辐射是由具有一定动能的自由电子经过高电荷态离子近旁时，被离子捕获复合成较低电荷态离子，同时产生的辐射.复合辐射(自由-束缚)与光电离(束缚-自由)互为逆过程，借助复合辐射截面(自由-束缚碰撞截面)与光电离截面的Milne关系[14]：

(11)

其中，σbf为光电离截面，σfb为复合辐射截面，ve为电子的速度，Eγ是辐射光子的能量，ω0是复合前离子的基态的统计权重，ωi是复合后离子的能级i的统计权重.

复合辐射过程产生的辐射可由光电离截面求得.本文中的复合辐射计算包含了Verner等[15]计算的基态光电离截面和Karzas等[16]计算的激发态光电离截面.复合辐射可由下式表述：

(12)

(13)

双光子辐射是指电子由激发态辐射两个光子回到基态，该过程对于较低电子密度的类氢和类氦等离子体尤为重要.光学薄条件下的双光子辐射过程产生的辐射采用Young等人[17]工作中(11)式表述，双光子辐射由下式表述：

(14)

其中，Aji为辐射跃迁速率，Ael为元素的相对丰度，FZj为电荷态为j的离子在温度T下对应的电荷态分布数据，Nj(X+q)为处于能级j的带+q电荷的离子的数密度，λ为波长，ne为电子密度，λ0为激发态与基态间能量差对应的波长，λ0/λ表示波长为λ的光子的能量与对应的激发态与基态间能量差的比值，φ(λ0/λ)为谱分布函数[18，19]，即双光子跃迁速率随光子能量的分布.

3 碰撞电离平衡模型结构及其应用

图1为SasalPy的碰撞电离平衡模型的理论概述图，碰撞电离平衡模型主要包括电离平衡计算或者电荷态分布计算(Charge stage distribution，简称CSD)、线辐射率计算(Line emissivity)、连续辐射率计算(Continuum emissivity)、合成光谱(Spectrum)以及辐射损失(Radiative loss)计算，对应的程序模块依次为getCsdCie、getLineEmiss、getContEmiss、getSpectrum和getRadLoss.图中E-E是电子碰撞激发过程，Ph-E是光子激发过程，P-E是质子激发过程，DI是直接碰撞电离，EAI是激发自电离过程，RR是辐射复合过程，DR是双电子复合过程，TBR是三体复合过程.

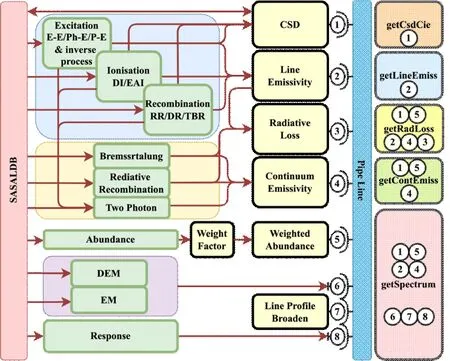
图1 SasalPy碰撞电离平衡模型理论概述图.数字序号表示不同程序接口与模型最上层模块的关联性

Abundance是天体元素丰度，微分发射度(Differential emission measure，简称DEM)和发射量度(Emission measure，简称EM)是理论光谱与观测光谱建立联系的关键参数，用于描述天体X射线辐射源温度结构与发射量度之间的关系[20，21].Response由观测望远镜的响应几率和有效面积组成，取决于望远镜的性能.Broaden表示光谱展宽的方法，一般采用高斯展宽.光谱合成计算基于线辐射率和连续辐射率计算结果，辐射率经由电离平衡(CSD)、元素丰度(Abundance)与DEM或EM加权求和，而后经过展宽(Broaden)或与仪器的响应(Response)卷积便可得到模拟的合成光谱.图2演示SasalPy获取光谱的流程(以Fe XIV为例)：

图2 SasaPy获取Fe XIV离子光谱的演示

1.第一步(stage 1)丰度数据设定，对应图1中的序号5；

2.第二步(stage 2)电离平衡数据设定或计算，对应图1中的序号1；

3.第三步(stage 3)获取特定温度、密度网格有限波长范围内的线辐射率数据，通过参数read选择计算(read=0)或者读取(read=1)相应数据，对应图1中的2；

4.第四步(stage 4)调用光谱合成模块(getSpectrum)计算，计算前需设定波长网格(lambgrid)和谱线展宽(instrBroaden)，通过参数doContinuum设定是否包含连续辐射计算，photons参数用于设定输出单位形式(photons=1时单位为光子形式)；

5.第五步(stage 5)显示光谱结果.

以上从程序层面简要描述了getSpectrum获取光谱的过程，下面将进一步描述各个模块的实现情况.

3.1 电离平衡计算

电离平衡计算模块(getCsdCie)核心计算过程主要在于求解由微观物理过程中的速率系数构成的速率方程，由碰撞等离子体主导的电离平衡计算主要考虑的微观物理过程主要有电子、质子与粒子的碰撞激发及其逆过程、直接碰撞电离、激发自电离、双电子复合、辐射复合和电荷交换.电荷交换过程暂未包含到模型中来，它将会在下一步工作中包含到模型中.SasalPy使用Scipy中的bicg求解速率方程AN=0，以一维单位向量作为bicg求解时的初始猜测，减少求解所需的迭代次数.电离平衡条件下的电荷态分布结果表明，元素从中性至裸离子的离化产生限于一定的温度范围，定义该温度范围为该元素的电荷态分布的有效温度范围.图3给出了高能天体物理研究中所关注的30号元素的电荷态分布的有效温度范围，温度低于有效范围，元素将以中性粒子形式存在，元素电离度低；温度高于有效范围，元素将以裸离子形式存在，元素电离度高.

图3 原子序数30以内的元素的电荷态分布的有效温度范围

除了了解元素的电荷态分布的有效温度范围外，了解元素对应的所有电荷态离子在电离平衡条件下存在分布的温度范围也很重要，该温度范围有助于模型判断特定温度下在计算中需要考虑的离子，参考该温度范围，程序在运算过程中自动判断选择需要加载的离子参数，可以有效节省运算时间.SasalPy取0.001作为电荷态分布的最小值，保留离子的电荷态分布大于0.001的温度区间内的数据.

图4是SasaPy计算的氧和铁的电荷态分布与Chianti数据库[22]、AtomDB数据库[23]以及梁贵云等人[24]计算的电荷态分布的对比.其中，氧元素在低温区域(<105K)随着温度的降低，本文计算的电荷态分布与Chianti[22]、AtomDB[23]和梁贵云等[24]的结果随着温度的降低表现出的差异性逐渐增大，此温度区间主要介于红外波段与紫外波段之间，氧元素低电荷态离子(O I、O II、O III)对X射线波段影响很小，此处的差异可以忽略；SasalPy计算的位于高温区域(>105K)的氧离子与Chianti[22]、AtomDB[23]的结果符合的很好，与梁贵云等[24]表现出的差异主要是因为其计算结果对应的温度网格较为稀疏，对比中由插值计算带来的影响，但梁贵云等[24]的实际计算值与SasalPy能够很好的符合.由于Chianti[22]、AtomDB[23]和梁贵云等[24]计算的电荷态分布结果对应的温度范围仅介于104—109K之间，超出此温度范围的结果由外推法插值计算获得，SasalPy计算的铁元素的电荷态分布与前述三种结果在低温区小于104K处表现出的较大差异主要由插值计算引起，温度越低则插值精度越低，差异越大.如上述氧的讨论中所述，处于更低温度的低电荷态铁离子对X射线波段的影响可以忽略.Urdampilleta等人[25]认为电荷态分布数据之间差异小于10-20%是好的符合.按照相同的评定标准，在低温区(104—105K)：SasalPy计算的Fe II、Fe III和Fe IV的电荷态分布与AtomDB、Chianti和梁贵云等人的结果符合的较好，本文计算的Fe V的结果与Chianti和梁贵云等的结果符合的很好，与AtomDB结果的离子比例峰值相差24.8%；在高温区(107.5—109K)：本文计算的Fe XXV、Fe XXVI和Fe XXVII与AtomDB、Chianti和梁贵云等符合的很好；在温度区域105—107.5内：SasalPy计算的结果与AtomDB、Chianti和梁贵云等人的结果差异明显，其中Fe XV的离子比例峰值达到了梁贵云等人结果的2.2倍.

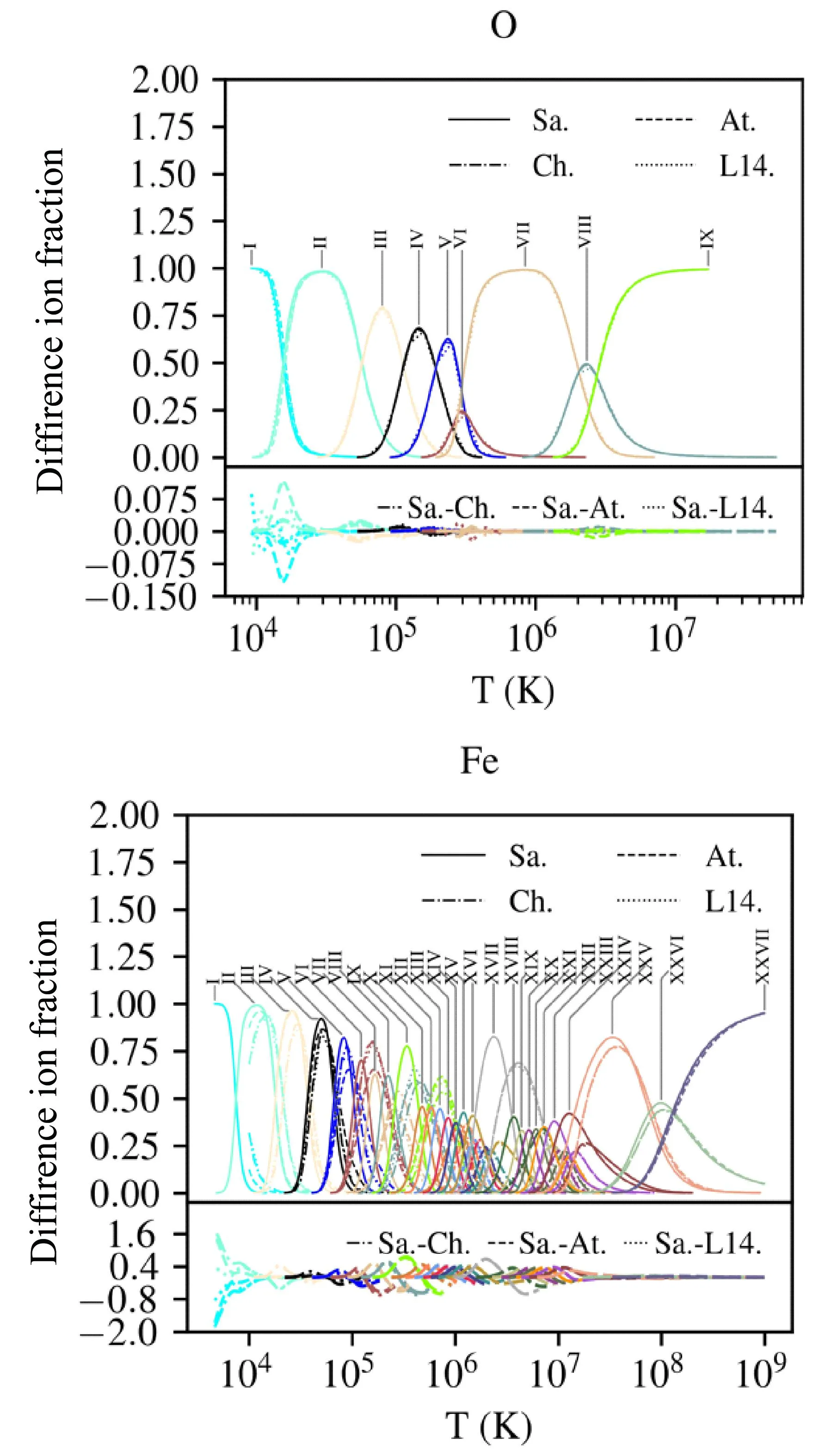
图4 元素氧和铁的电荷态分布.Sa.表示由SasalPy计算的电荷态分布结果，Ch.表示Chianti数据库中的电荷态分布结果(chianti.ioneq)，At.表示AtomDB数据库中3.0.7版本电荷态分布结果，L14.表示梁贵云等计算的电荷态分布结果，图中底部描述的是Sa.与其余三者的差异，即不同模型结果的差值.不同的颜色表示不同的电荷态的离子

电离平衡数据即电荷态分布作为线辐射、连续辐射计算的重要参数，该参数中存在的误差会影响光谱的计算结果.电离平衡取决于电离过程和复合过程，电离速率和复合速率基于理论计算和实验测量产生，理论计算时能级的选取和能级数据的限制以及实验测量误差均会对电离和复合速率产生影响，同时不同的理论模型也会引入一定的系统误差，这就导致了各个模型收录或者计算的电离平衡数据存在差异[26].为了进一步对电离平衡数据进行差异性探讨，本文选取氧和铁元素的类氦离子的电离平衡数据进行对比，O VII和Fe XXV对X射线波段的贡献高于附近其他电荷态的离子.具体做法是，以SasalPy计算的电离平衡数据为基础，选取各离子电离平衡数据大于0.001的温度范围，对不同的电离平衡数据进行对比，见图5.为了方便对比，本文在温度范围内以插值的方法统一温度网格.

图5 氧和铁类氦离子不同数据来源的电离平衡数据对比.Sa.、Ch.、At.和L14.表示的含义与图4相同

SasalPy计算的类氦氧离子(O VII)的电荷态分布与Chianti、AtomDB以及梁贵云等计算的结果符合的很好，对比中表现出的振荡式的差异曲线主要由于插值计算引起，由于梁贵云等计算的结果采用的温度网格较其余三者稀疏，差异曲线表现出的振荡程度最强，表明更加精细的温度网格有助于提高电荷态分布结果的精确性.SasalPy计算的类氦铁离子电荷态分布在曲线上升部分与Chianti、AtomDB以及梁贵云等的结果差异明显，本文计算的结果与Chianti和AtomDB最大相差64.7%，与梁贵云等的结果最大相差65.2%；对于曲线下降部分本文结果与Chianti和梁贵云等的结果最大相差13%，与AtomDB最大相差21.6%.Heuer等[26]以PyAtomDB为基础通过数值模拟的方法指出系统误差与温度偏移存在着联系.类氦铁离子的电荷态分布曲线表明SasalPy计算的电荷态分布曲线峰值温度相比AtomDB、Chianti、梁贵云等的结果向低温区产生了偏移.SasalPy采用的电离平衡计算方法与梁贵云等[10]人的方法相似，主要不同的地方在解AN=0线性方程时采用的方法不同，SasalPy主要应用Python第三方库Scipy中的bicg函数求解方程，而梁贵云等人采用的是IDL语言中的LINBCG函数求解方程.此外，SasalPy与梁贵云等人采用了相同的电离速率数据和复合速率数据，本文计算的电荷态分布与梁贵云等的结果的差异可能由求解线性方程组的方法不同引起.

SASALDB数据库除了本文计算的电离平衡数据外，还收录了多种电离平衡数据供用户选择，详见表1.

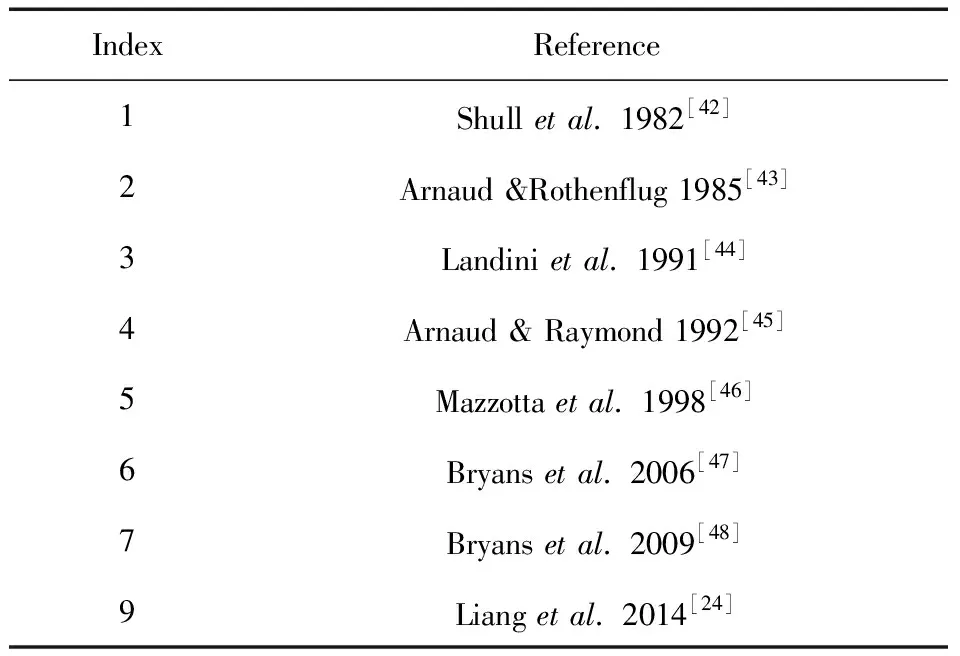
表1 SASALDB收录的其他电荷态分布数据

3.2 线辐射率计算

线辐射率计算模块(getLineEmiss)旨在计算线辐射率随波长或者能量的分布，计算核心在于求解某一电荷态离子某一能级j的归一化的能级布居，求解能级布居时需考虑电子和质子与离子的碰撞激发及去激发、辐射复合和双电子复合、直接碰撞电离以及激发自电离的影响.解得的能级布居与辐射跃迁速率、光子能量的乘积即是线辐射率，如(5)式所示.对于热等离子体来讲，线辐射的贡献是不容忽略的.原子参数的不同影响线辐射率计算，例如能级能量、辐射跃迁速率、碰撞强度的不同会对线强产生显著影响.图6是类氦碳离子C V在10—60 Å波段内对线辐射贡献较大的四种跃迁在单一温度(106K)低密度条件下的线辐射结果.图中标注的四种跃迁根据波长由短到长对应的上能级分别是1s3p1P1、1s2p1P1、1s2p3P1、1s2s3S1，跃迁对应的下能级均为1s21S0.表2列出了四种跃迁在SASALDB与Chianti数据库[22]中对应的能级、波长、辐射跃迁速率(A Value)和差异以及四种跃迁对应的有效碰撞强度.

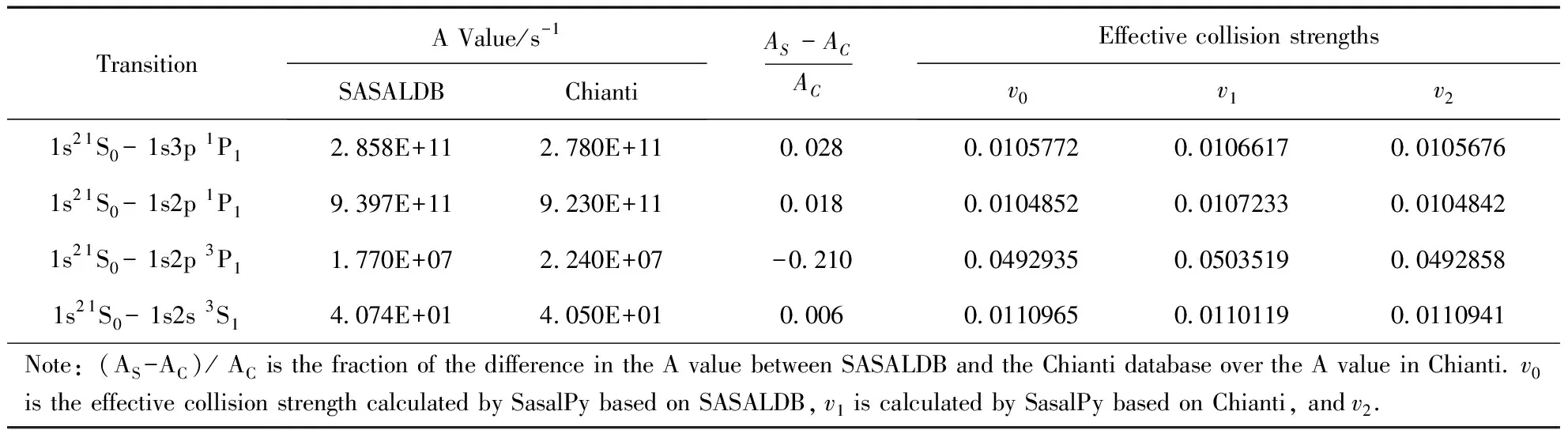
表2 C V四种跃迁对应的辐射跃迁速率和有效碰撞强度

图6 C V四种跃迁的线辐射率.Ch.C V是使用ChiantiPy基于Chianti数据库计算的结果；Sa.1 C V是SasalPy基于SASALDB数据库计算的结果；Sa.2 C V是SasalPy使用Chianti数据库中C V的能级数据与辐射跃迁速率计算的结果；Sa.3 C V表示的结果中SasalPy使用了Chianti数据库C V的碰撞强度；Sa.4 C V表示的结果中SasalPy同时使用了Chianti数据库中C V的能级能量、辐射跃迁速率以及碰撞强度数据

从图6中可以看到，SasalPy与ChiantiPy对于跃迁1s21S0-1s3p1P1的线辐射率计算结果符合的很好.跃迁1s21S0-1s2p1P1对应的Ch.C V、Sa.1 C V、Sa.2 C V线辐射符合的较好，Sa.3 C V由于使用Chianti数据库的碰撞强度，线辐射率相比Sa.1 C V提升了4.74%；同理，Sa.4 C V由于碰撞强度不同的影响相比Sa.2 C V提升了30.95%；Sa.2 C V由于使用Chianti数据库的能级能量和辐射跃迁速率数据，线辐射率相比Sa.1 C V降低了0.078%，变化可以忽略；Sa.4 C V由于能级能量和辐射跃迁速率不同的影响相比Sa.3 C V提升了24.9%.对于跃迁1s21S0-1s2s3S1，Sa.3 C V相比Sa.1 C V提升了0.78%，Sa.4 C V相比Sa.2 C V降低了1.18%；Sa.2 C V相比Sa.1 C V提高了4.03%，Sa.4 C V相比Sa.3 C V降低了16.25%.对于跃迁1s21S0-1s2p3P1，碰撞强度数据的不同导致Sa.3 C V相比Sa.1 C V提升了18.5%，Sa.2 C V和Sa.4 C V与ChiantiPy符合的很好.对比结果表明，原子参数如辐射跃迁速率、有效碰撞强度对于较强跃迁的线辐射率计算会有显著影响.

3.3 连续谱辐射率计算

连续谱辐射率计算模块(getContEmiss)同以上描述的电离平衡计算模块和线辐射率计算模块是碰撞电离模型的核心计算模块，进一步的光谱合成计算模块和辐射损失计算模块将依赖于这三个模块的运算结果.连续辐射主要包括轫致辐射、复合辐射以及双光子辐射.

图7为SasalPy与ChiantiPy在温度为106K和低密度(1 cm-3)条件下的连续谱结果对比，SasalPy与ChiantiPy使用了相同的丰度数据[27]和电荷态分布数据，电荷态分布数据使用Chianti数据库[22]中的chianti.ioneq文件.可以看到，SasalPy与Chianti在轫致辐射和复合辐射计算上符合的很好，SasalPy的轫致辐射在应用Nozawa等[11]计算的相对论冈特因子的基础上，用Sutherland等[13]提出的冈特因子进行了修正，方法与Chianti选用的方法相同.对于复合辐射，SasalPy和ChiantiPy应用相同的光电离截面，即Karzas等计算的光电离截面[16].轫致辐射及复合辐射存在微量的差异，一方面是因为SasalPy和ChiantiPy在处理相关系数时约化取值存在不同，例如SasalPy中光速取值为2.997825×1010cm·s-1，而ChiantiPy中取值为2.99792458×1010cm·s-1，再如根据hc/λ对波长进行单位转换时(KeV与Å相互转换)，SasalPy对hc的取值为12.398，ChiantiPy对hc的取值为12.39841875；另一方面是因为SasalPy与ChiantiPy在电荷态分布数据插值方法上的不同，为了避免插值计算时负值的出现，SasalPy在电荷态分布数据插值取值时将其转换为以10为底的对数进行插值计算，ChianitPy则是将电荷态分布数据转换为以e为底的对数进行插值计算，最终的结果在合理的误差范围.对连续谱差异贡献最大的主要是双光子辐射.双光子辐射主要包括类氢和类氦离子的贡献.引起双光子辐射差异的主要是类氦离子，类氢碳离子和类氦碳离子在双光子辐射中贡献最多，以下以C V和C VI为例分析双光子辐射的差异.双光子辐射计算中，SasalPy与ChiantiPy使用相同的谱分布数据[18，19]，即相同的谱分布函数φ(λ0/λ)，见(14)式.

图7 SasalPy与ChiantiPy连续谱对比.图中Ch.total和Sa.total分别为ChaintiPy和SasalPy总的连续谱结果；Ch.ff和Sa.ff对应的是轫致辐射；Ch.fb和Sa.fb对应的是复合辐射；Ch.tp和Sa.tp对应的是双光子辐射

图8左图是类氢碳离子C VI的双光子辐射对比，Ch.C VI tp是ChiantiPy的计算结果，ChiantiPy在106K时对应的经插值后C VI的电荷态分布数据为0.5855，Sa.C VI tp a是SasalPy的计算结果，SasalPy在106K时对应的经插值后的C VI电荷态分布数据为0.5481，仅由插值方法不同引起的差异为6.4%.Sa.C VI tp b是SasalPy使用与ChiantiPy相同的电荷态分布数据0.5855计算的结果，SasalPy与ChiantiPy在使用相同的差值方法后结果符合的很好，说明C VI的双光子辐射差异仅由插值方法的不同引起.图8右图是类氦碳离子C V的双光子辐射对比，Ch.C V tp是ChiantiPy的计算结果，ChiantiPy在106K时对应的经插值后C V的电荷态分布数据为0.2677，Sa.C V tp a是SasalPy的计算结果，SasalPy在106K时对应的经插值后的C V电荷态分布数据为0.2744，此时仅由差值方法引起的差异为2.5%，但是与由能级数据和辐射跃迁速率引起的差异相比，可以忽略不计.Sa.C V tp b是SasalPy使用与ChiantiPy相同的辐射跃迁速率和能级数据计算的结果.可以看到，SasalPy采用与ChiantiPy相同的辐射跃迁速率与能级数据得到的结果与ChiantiPy符合的很好，但Sa.C V tp b与Ch.C V tp依然存在18.4%的差异，这是由于SasalPy与ChiantiPy的数据库收录的C V的电离、复合以及碰撞强度数据不同导致的.相比由辐射跃迁速率与能级数据不同引起的差异，由C V的电离、复合以及碰撞强度数据不同导致的差异可以忽略.对于C V，SasalPy的数据库中目前仅收录了主量子数n=2-4的49个能级的数据[28]，Chianti数据库收录了主量子数n=2-8的577个能级[29-31].图9中SasalPy与ChiantiPy的数据库收录的C V的辐射跃迁速率在10-16 Å波段的对比表明SasalPy的辐射跃迁速率多数小于Chia-ntiPy，SasalPy在求解能级布居时自发辐射对能级布居的影响远小于ChiantiPy，故由SasalPy计算的C V的能级布居结果要远大于ChiantiPy，进而使得由SasalPy计算的C V的双光子辐射Sa.C V tp a高于ChiantiPy的结果Ch.C V tp.

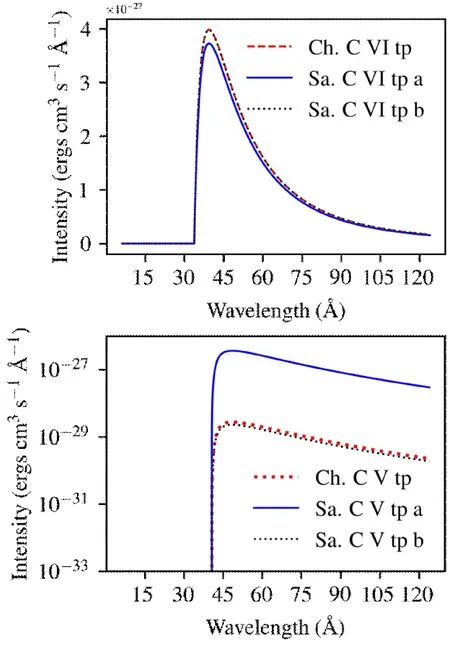
图8 C VI与C V由不同等离子体模型计算的双光子连续谱对比.上图是类氢碳离子C VI的双光子辐射对比，Ch.C VI tp是ChiantiPy的计算结果，Sa.C VI tp a是SasalPy的计算结果，Sa.C VI tp b是SasalPy使用与ChiantiPy相同的电离平衡数据计算的结果；下图是类氦碳离子C V的双光子辐射对比，Ch.C V tp是ChiantiPy的计算结果，Sa.C V tp a是SasalPy的计算结果，Sa.C V tp b是SasalPy使用与ChiantiPy相同的辐射跃迁速率和能级数据计算的结果

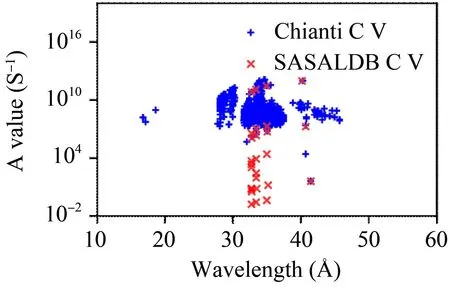
图9 C V在10-60 Å波段来自不同数据库的辐射跃迁速率对比

3.4 合成光谱

图10 6.199-123.985 Å波段内的合成光谱.光谱b的温度为106.125 K，DEM数值为0.23，电子密度为2×108 cm-3；光谱c的温度为106.875 K，DEM数值为6.99；光谱d的温度为107.525 K，DEM数值为0.53，光谱c和d的电子密度同为1012 cm-3；光谱a为光谱b、c、d的合成谱，DEM的单位见右图.右图中三个颜色区域由左至右依次对应低温区、中温区和高温区

3.5 辐射损失

辐射损失计算模块(getRadLoss)主要用于计算由微观物理过程引起的等离子体能量损失随温度的分布.辐射损失计算的核心计算主要是线辐射率的计算和连续辐射率的计算，在考虑连续辐射的影响时，仅考虑轫致辐射和复合辐射的贡献.随着X射线光谱仪性能的不断提升，使得我们可以观测到更为精细的天体结构信息.与此同时，新的观测数据向等离子体模型提出了挑战.新的观测数据捕捉到的精细天体结构信息需要合理的等离子体模型和更加精确的原子数据进行解析.不同的等离子体模型由于其本身采用的理论和近似方法以及原子数据的不同，在辐射损失计算时会表现出明显的差异性[33].图11是SasalPy与不同的等离子体模型的辐射损失或冷却曲线的对比.

图11 不同等离子体模型之间的辐射损失对比.Sa.表示SasalPy的计算结果，Ch.表示Chianti的计算结果，Sp.表示SPEX的计算结果，Cl.表示Cloudy的计算结果，At.表示PyAtomDB的计算结果，Sc.表示Schure等人的计算结果

图11中SPEX、PyAtomDB、Cloudy、Schure四种等离子体模型的辐射损失或冷却曲线源自于Stofanova等人[33]的工作.表3汇总了不同等离子体模型在辐射损失计算中使用的丰度数据和电荷态分布数据.

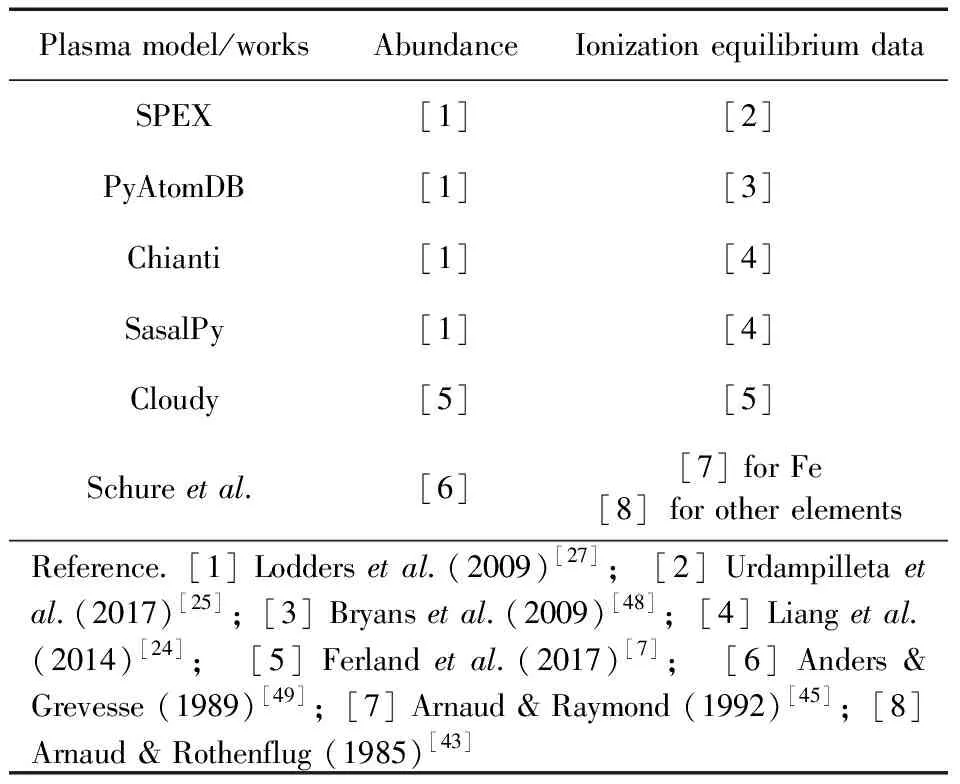
表3 不同等离子体模型计算辐射损失使用的丰度数据与电离平衡数据

SASALDB数据库目前更新了类碳[34]、类氮[35]、类氧[36]等电子系以及类氢离子和类氦离子[37]的理论碰撞激发数据，即能级数据、辐射跃迁速率以及碰撞强度.通过NIST数据库[38]的实验能级数据对SASALDB中的离子的波长进行了修正.SasalPy的辐射损失结果是基于更新后的数据库得到的，辐射损失计算用到的具体离子见图12.将辐射损失以0.1 keV为界限将辐射损失结果分为两部分进行讨论.可以看到，当温度大于0.1 keV时，SasalPy的辐射损失结果与PyAtomDB在这一部分符合的很好.SasalPy与Cloudy在0.1-10 keV范围符合的很好，大于10 keV时差异增大，差异最大达到29.4%.在高温区(大于0.1 keV)，连续辐射中的轫致辐射主导地位加深，Stofanova等人[33]认为，由于不同的等离子体模型的轫致辐射采用不同修正方法计算的冈特因子，例如非相对论、半相对论和相对论修正等，会导致不同程度的差异.SasalPy的轫致辐射采用Nozawa等[11]计算的经过相对论修正的冈特因子，这一点与PyAtomDB和Chianti的辐射损失结果采用的冈特因子相同.SasalPy与PyAtomDB的辐射损失结果在高温区符合的很好，差异最大为8.25%，出现在温度最高处.Chianti的辐射损失在高温区略低于SasalPy，温度最高处与SasalPy的差异为7.24%，此处差异最大.在0.1-10 keV范围内主导辐射损失的为线辐射，SasalPy与SPEX、Schure等[39]差异变化明显是因为不同等离子体模型采用的线辐射计算的基本参数不同，这其中辐射跃迁速率和碰撞强度数据的不同导致的影响不可忽略.SasalPy在高温区与SPEX、PyAtomDB、Chianti以及Schure等人[39]的辐射损失表明，SasalPy在X射线波段的数据是足够精确的.

图12 SasalPy辐射损失计算用到的离子.蓝色的五角星表示SASALDB原始离子数据，紫色方块表示更新后的离子数据；q是离子所带电荷量

当温度小于0.1 keV时，辐射损失主要由线辐射里的碰撞激发过程主导.在0.002-0.1 keV范围内，SasalPy的辐射损失相比于其他等离子体模型最小.在0.001-0.015 keV范围氢原子的贡献占据主导地位，Stofanova等人[33]认为氢原子的碰撞强度的不同对氢原子对辐射损失的影响较大，他们换用Chianti数据库[1]新的氢原子碰撞强度，氢原子对辐射损失的贡献在温度为2 eV处的减少了3倍，得到了与PyAtomDB与Cloudy符合较好的结果.SASALDB中氢原子的碰撞强度采用的是未修正过的Anderson等[40]计算的数据.因此，SasalPy在0.015 keV左右相比其他等离子体模型要低很多.随着SASALDB数据库的碰撞激发数据的更新，SasalPy在小于0.1 keV的温度范围将会有所改善，相关工作将会在后续工作中开展.经过上述分析，从不同等离子体模型的辐射损失结果表现出的差异性来看，等离子体模型和原子数据的持续精确地更新研究是尤为重要的.

4 结 论

提出了一种新的基于Python语言的适用于高能X射线的等离子体模型SasalPy，简要阐述了SasalPy的碰撞电离平衡理论，主要就碰撞电离平衡模型总体框架和电离平衡计算、线辐射率计算、连续辐射率计算、合成光谱及辐射损失计算五个重要模块作了详细描述，从功能性或差异性方面说明了SasalPy的可用性和精确性.此外，电离平衡计算对氧元素和铁元素对比讨论表明，由SasalPy的电离平衡计算的氧元素和铁元素的部分温度区域的结果与其他等离子模型高度相符.另外，通过对比来自不同数据源的类氦离子电荷态分布数据，可以为用户选取电离平衡数据提供参考.线辐射计算中对C V四种跃迁产生的线辐射率的讨论表明，原子参数如跃迁速率、碰撞强度等的不同会对线辐射率和线强产生影响.对于这种现象，SasalPy的未来版本将支持用户选择并测试不同的原子物理数据，填补目前其他等离子体模型不具备的功能应用空缺.SasalPy与ChiantiPy的连续谱的对比表明，由辐射跃迁速率数据的不同产生的影响对类氦碳离子的双光子辐射不可忽略.采用Capella星冕的低、中、高三个不同温度区域的体微分发射度，实现了光谱合成应用.SasalPy与PyAtomDB、SPEX、Chianti、Cloudy以及Schure等人的辐射损失对比表明，Sasalpy在X射线能段的数据与其他等离子体模型极度相近.SasalPy作为自主研发的新一代等离子体模型将会为由我国主导的下一代X射线高分辨能谱空间望远镜[41](Hot Universe Baryon Surveyor，简称HUBS)的高分辨率X射线光谱分析提供有力支持，该模型在高能X射线研究领域具有较高的应用价值.