基于热电制冷的微流体线性降温特性研究

王好卿 孙东方, 高 才 程文龙 周 培 唐景春 朱俊叶 韩 雪 张梦飞

(1 合肥工业大学汽车与交通工程学院 合肥 230009;2 中国科学技术大学工程科学学院 合肥 230026)

微流控芯片又称为“芯片实验室”,可以简化复杂生物医学、化学等研究,开展批量样品筛选和处理,显著减少分析样品量,提高研究的可预测性和可控性,在人工生物膜制备及细胞分析方面具有独特的优势[1-3]。然而,在对生物微流体的操控过程中,不仅需要准确控制微流体的成分比,还必须要进行精确的温度调控[4-5],尤其是微流体温度以恒定速率变化的线性温度调控。对于冷冻保存,除细胞化学环境外,冷冻和复温过程中的细胞存活率也取决于冷却和复温速率。为了避免细胞内结冰或高电解质浓度引起的冷冻损伤,需要以最佳温度变化速率对样品线性降温或复温[6]。

目前,微流控芯片室温以上的加热问题已被很好地解决,例如红外加热[7]、激光加热[8]、微波加热[9]和薄膜电加热[10-11]等。但微流控芯片室温以下的降温,尤其是线性降温方面仍面临挑战。为研究升降温速率对细胞膜渗透性的影响,Peng Ji等[12]设计了一种集成冷却微通道与薄膜加热组件的微流控芯片实现了生物微流体在2～37 ℃间的恒温控制。R. M. Guijt 等[13]通过微通道内丙酮蒸发吸热,获得了1 ℃/s的冷却速率。这些方式在一定程度上满足了生物微流体的冷却需求,但考虑到复杂的结构、较高的成本以及加工工艺问题,在应用中仍有一定的局限性。

基于珀尔贴效应的热电制冷技术,在直流电流驱动下实现能量转换,可提供精确温控,并且具有尺寸可控、易集成、成本低、响应快等优点[14-16]。诸多研究表明热电制冷在微流体冷却方面具有独特优势。M. D. Tarn等[17]开发了一种使用3个热电制冷器(TEC,thermoelectric cooler)控制反应室温度的微流体平台,用于冻结连续流动中的液滴并分析大气中的冰成核颗粒。朱江等[18]基于热电制冷实现了对微流体的快速冷却,并通过数值模拟和实验测试研究了该温控系统的温度响应特性。L. Bahari 等[19]使用TEC和散热器获得了-5～5 ℃的温度梯度,然后用电动执行器移动样品载片,实现了细胞的定向冷冻。这些研究集中于热电制冷在微流控芯片室温以下的恒温控制方面的应用,而基于热电制冷的微流体线性降温仍需探索。

本文以样品观测微流控芯片(用于观测液滴或细胞的生成及保存)为依托,探索基于热电制冷的微流体线性降温特性。建立了热电冷却微流体芯片的多物理场仿真模型,并搭建了热电冷却微流体的实验测试系统,验证仿真模型的正确性。通过仿真,分析不同电流曲线下微流体的温度响应特性,探讨热电冷却微流体的线性降温特性并通过实验进行验证。

1 数值方法

1.1 热电冷却微流控芯片理论模型

为分析在不同电流下热电冷却微流控芯片的降温速率变化情况,本文建立了基于热电制冷的微流控芯片冷却系统,如图1所示。其中,为了冷却的同时实现微流体目标区域的光学观察,采用定制的中间开孔的TEC,TEC外径为25 mm,孔径为4 mm,厚度为3.2 mm;微流控芯片由聚二甲基硅氧烷(PDMS,polydimethylsiloxane)和载玻片基底组合制成,PDMS的整体尺寸为25 mm×50 mm×3.5 mm,微流体流道宽度为300 μm,中央样品池直径为1 mm,流道长度为20 mm,流道深度为300 μm。为测量样品池温度,本研究在微流控芯片侧边开设一个宽和高均为0.3 mm的测量孔,将T型热电偶插入样品池中央,并将孔口封闭,实现对样品池温度的测量,如图1中微流控芯片A-A截面图所示。

图1 热电冷却微流控芯片

1.2 热电制冷基本方程

热电制冷器通常由多对 P、N 型半导体构成的热电偶电串联、热并联组成,TEC热电偶如图2所示。当电流流过热电偶元件时,冷结处会立即产生珀尔贴冷却效应,热结处会因珀尔贴效应而释放珀尔贴热量。同时,考虑到电流与温度梯度,热电偶元件内部将产生焦耳热和汤姆逊热。此外,由于傅里叶效应,部分热量将从热电偶元件热端回流到冷端。因此,TEC的净冷却能力通常是由珀尔贴效应、傅里叶热传导、焦耳效应和汤姆逊热效应的协同结果。

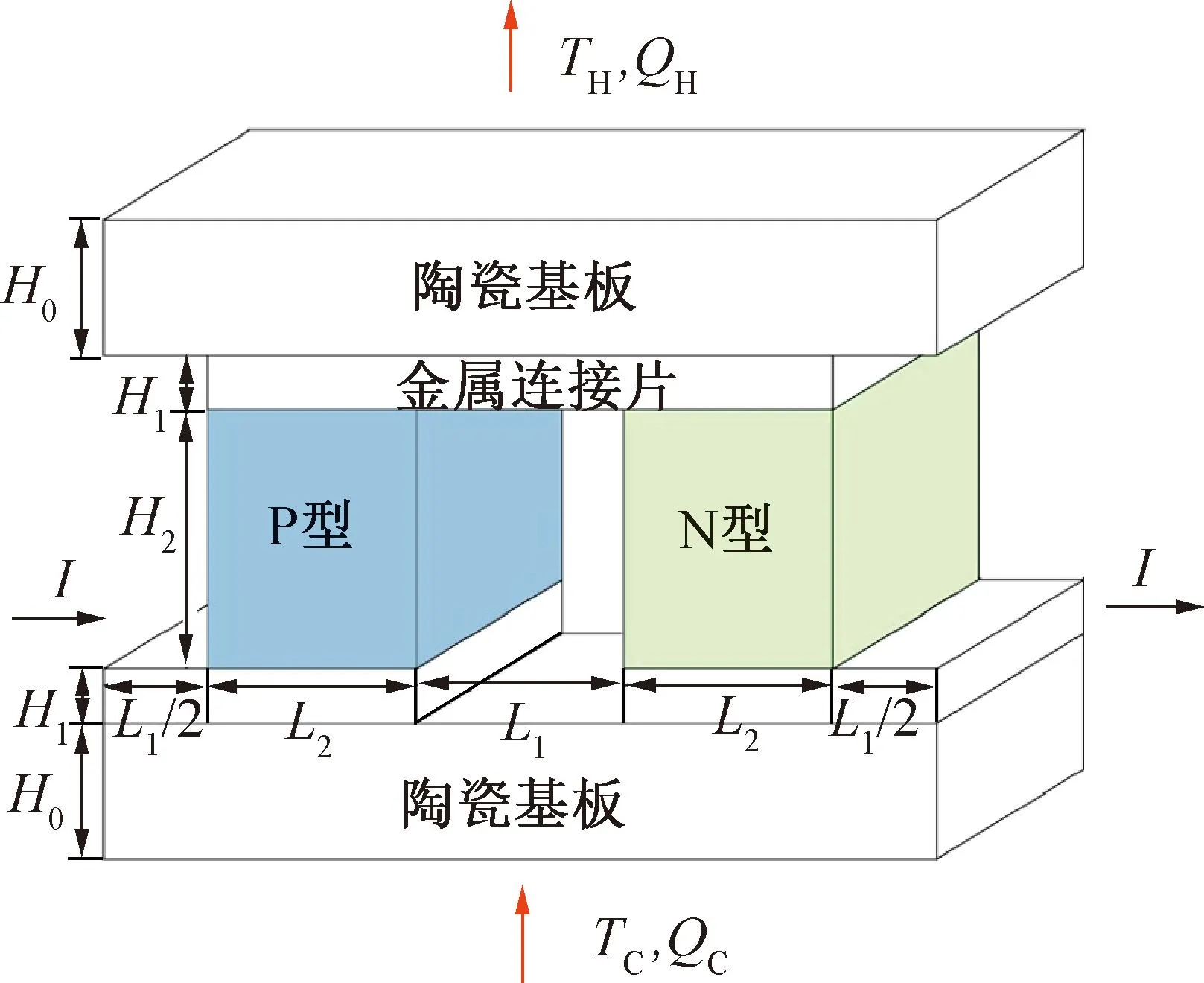
图2 TEC热电偶

由于辐射和TEC内部的热对流造成的热损失与TEC的制冷量相比非常小,因此本研究忽略了辐射和TEC内部对流引起的热损失。通过耦合电流场与温度场,建立TEC的数值瞬态模型,控制方程如下所述。

考虑到能量平衡,瞬态热扩散控制方程可描述为:

(1)

式中:cp为比定压热容,J/(kg·K);ρ为密度,kg/m3;T为温度,K;t为时间,s;q为热通量,W/m2;Q为内部产生的体积热,W/(m2·K)。考虑到珀尔贴效应和傅里叶热传导,q可通过下式计算:

(2)

式中:J为电流密度,W/m2;αS为塞贝克系数,V/K;k为导热系数,W/(m·K)。式(1)可表示为:

(3)

式中:σ为电导率,S/m;β为汤姆逊系数,V/K。汤姆逊系数与塞贝克系数相关,可表示为:

(4)

对于电输运过程,电流守恒公式为:

(5)

式中:D为电通量密度,V/m。为了包含热电效应,可通过本构方程(6)将热扩散和电流守恒方程进行耦合。

(6)

1.3 降温过程的线性度评价指标

本研究使用实际降温曲线相较于线性降温目标曲线的拟合优度R2为降温过程的线性度的评价指标,表示为:

(7)

2 实验方案

2.1 实验装置

为提高仿真模型准确性,探究非稳态热电转换规律并验证线性降温机制的准确性,本研究建立了基于热电制冷的微流体温度调控实验测试系统,如图3所示。系统基本工作流程如下:微流体通过注射泵进入微流控芯片样品池,TEC位于微流控芯片样品池的正上方,实现对样品池的冷却降温,如图3(b)所示;TEC热端与中间预留观测孔的紫铜水冷头相连,紫铜水冷头与恒温水槽连接,对TEC热端进行散热;热接触面均涂有导热硅脂以降低接触热阻;通过可编程直流电源驱动TEC工作,并控制供电电流的波形实现对降温过程的调控;在微流控芯片的侧边埋设微型T型热电偶,连接温度数据采集仪记录样品池中微流体温度的变化过程,温度测量间隔为3 s。此外,微流控芯片底部通已预冷后的氮气进行强制对流保证降温过程不受环境温度影响,同时避免结霜影响显微镜的观察。

图3 实验系统

2.2 误差分析

本研究对温度测量的不确定度进行了分析,温度测量的不确定度取决于测量设备的不确定度。实验所用仪器精度如表1所示,微流控芯片温控系统温度测量的误差分析如下:

表1 实验设备误差

TEC和微流控芯片的温度均通过T型热电偶测得,通过数据采集仪在电脑中进行收集并分析,根据该热电偶的性能参数,查得测温范围为-200～200 ℃,不确定度为0.5 ℃,同时数据采集仪有0.3 ℃的不确定度,因此实验设备的相对误差η为:

(8)

式中:x1、x2分别为热电偶和数据采集仪的不确定度;m为热电偶量程。计算可得,η为0.2%,在实验允许范围内。

3 结果与讨论

3.1 仿真模型验证

通过热电模块物性测试实验测得热电模块的物性参数,为热电冷却微流控芯片模型提供数据支撑[20]。热物性测试过程中将界面的接触电阻和接触热阻等效计入热电臂的热物性,实验测得TEC热电臂的塞贝克系数α(V/K)、电阻率ρe(Ω·m)及导热系数ke[W/(m·℃)]分别为(-33～53 ℃):

α=(225 600-540.1T+1.471T2)×10-9

(9)

ρe=(114 700-1 800T+1.852T2)×10-11

(10)

ke=(248 300-297T-1.56T2)×10-5

(11)

经过实验获得仿真模型的等效边界条件为:实验中水冷头与恒温水槽相连接,其温度被设定为1.5 ℃,在仿真模型中将TEC热端边界条件等效为对流传热系数[6 200 W/(m2·℃)]来模拟水冷头的强制对流传热。同时,微流控芯片底部(样品池正下方)中心半径为12.5 mm的区域设置为与经预冷后氮气的强制对流,对流传热系数为20 W/(m2·℃);根据实验测量,氮气的温度设定为-8 ℃。其他表面与空气自然对流,对流传热系数设定为5 W/(m2·℃);仿真模型物性参数如表2所示。

表2 模型参数

在仿真分析前,首先对模型进行网格独立性验证,通过应用G1(12 849个网格)、G2(23 910个网格)、G3(38 018个网格)、G4(64 196个网格)、G5(87 119个网格)、G6(229 742个网格)、G7(338 386个网格)和G8(944 410个网格)8个网格系统进行网格独立性验证。图4所示为TEC最佳工作电流4 A下微流体样品池温度Tcen及TEC的冷、热端温差随着网格数增长的变化情况。由图4可知,当网格数大于G6时,数值之间的差异几乎不可察觉,数值结果与网格无关。因此,为了降低计算成本,本研究采用G6网格系统。

图4 网格独立性检验结果

通过实验对模型的有效性进行了验证。不同电流下微流体样品池温度数值模拟结果与实验结果对比如图5所示。恒定电流为2、3、4 A时,实验值与仿真值间的回归分析决定系数即吻合度分别为0.998 6、0.997 8、0.995 8,证实了建立的多物理场模型的有效性和合理性。

图5 不同电流下数值模拟结果与实验对比

3.2 恒定电流下微流体的温度响应

通过仿真获得TEC最佳工作电流4 A下,TEC冷端温度和微流体样品池中心温度的响应情况,如图6所示。由图6可知,TEC冷端最低温度为-41.257 ℃,微流体样品池中心最低温度为-30.784 ℃;TEC冷端在第 50 s时达到-30 ℃,而相比之下,微流体样品池中心温度直至约第150 s才达到该温度,这是由于 PDMS 导热系数低[0.159 W/(m·℃)]且比热容相对较大[1 460 J/(kg·℃)],冷量传导至样品池的时间很长,过长的温度响应迟滞时间会显著影响微流体的线性降温过程。此外,微流体样品池在0～400 s降温曲线的线性度R2为0.464,由此可知,施加恒定电流难以实现微流体线性降温的目标。

图6 恒定电流下的温度响应曲线

为进一步探究恒定电流下的热电转化规律,对微流体样品池降温过程的温度变化率进行分析。假设微流体的目标线性降温速率为20 ℃/min,施加4 A恒定电流时,微流体样品池的温度变化率如图7所示。微流体样品池的温度变化速率先是远大于20 ℃/min,而后逐渐下降,在50 s时降至20 ℃/min以下并继续下降,在100 s时趋近于0。这是由于对于确定的TEC,其工作过程中的制冷量主要取决于工作电流、 TEC冷端温度和冷、热端温差。随着TEC冷端温度的下降与TEC冷热端温差的增大,TEC的制冷量逐渐下降。因此,TEC冷端输入至微流控芯片中的冷量先是大于实现线性温度变化所需的冷量故而存在冷量的盈余,而后输入至微流控芯片中的冷量小于其所需冷量故而存在冷量的缺口。

图7 恒流下实际与目标温度变化率及冷量曲线

3.3 单一电流函数下微流体的温度响应

由3.2小节的分析可知,恒定电流下TEC冷端温度降低与冷热端温差变大会使TEC制冷量下降,因此为实现微流体线性降温的目标,应使输入电流逐渐增加。此外,对于稳态电流下运行的TEC,存在一个最佳电流以提供最低冷却温度[21]。本研究使用的TEC最佳工作电流为4 A,输入电流在逐渐增大至4 A后继续升高,电流无法继续提升TEC的冷却性能。

综上,本研究使TEC工作电流分别按照时间t的0.5次、1次、2次曲线逐渐增大,即电流曲线分别为f(t0.5)、f(t)、f(t2),且均在100 s时达到4 A,将电流自0逐步增至4 A的时间定义为最大降温时间tgen。由图8可知,当电流达到4 A时,f(t0.5)、f(t)、f(t2)电流驱动机制下微流体样品池温度的最低温度分别为-23.32、-19.86、-12.66 ℃,这是因为在0～100 s内TEC的功率不同,导致f(t0.5)电流驱动机制下微流体获得的冷量大于f(t)和f(t2)。经过分析还发现,f(t0.5)、f(t)、f(t2)电流驱动机制下微流体样品池降温曲线的线性度分别为0.993 4、0.988 8与0.951 3,降温速率分别为29.08、27.01、22.67 ℃/min。虽然单一函数电流驱动机制下相比于恒流下微流体的温度响应曲线线性度得到了提升,但各降温曲线相比于目标降温曲线均存在较大的冷量盈余与缺口。

图8 单一函数电流与温度响应曲线

3.4 线性降温的实现及实验验证

为了提升微流体降温过程的线性度,实现微流体的精准线性降温,通过仿真将3种电流曲线进行耦合。通过自定义电流曲线函数的方式控制驱动电流,分析微流体降温曲线并进行线性度检验与电流参数的迭代,具体方法如下:

以设定最大降温时间为80 s为例,即电流在第80 s到达最佳电流4 A,定义电流函数为:

I=αt2+βt+γt0.5

(12)

式中:α、β和γ分别为各个单一电流函数对应的系数。通过改变α、β和γ的大小使得非稳态过渡电流的电流曲线逐渐从与时间二次关系变化到0.5次关系,进而修正电流波形,逐渐弥补与降温曲线之间的冷量盈余与缺口。

通过仿真获得不同非稳态过渡电流驱动机制下的电流曲线及微流体降温曲线,如图9所示。其中,随着非稳态过渡电流曲线由f(t2)过渡至f(t)再过渡至f(t0.5),微流体降温曲线也随之变化。表3所示为不同非稳态电流驱动机制对应的系数及微流体降温曲线的线性度。由表3可知,随着系数α的下降与γ的增加,样品池最低温度逐渐下降,这是由于电流曲线逐渐由与时间的二次关系曲线转变为0.5次关系曲线,进而导致在固定时间内提供给微流体的冷量逐渐增加,能够将微流体样品池冷却至更低的温度。

表3 电流曲线系数及对应温度曲线线性度

图9 非稳态过渡电流曲线及微流体降温曲线

由表3还可知,随着α的降低,R2先增加后降低,当α=4.6×10-4、β=1.2×10-2、γ=0时,R2取得最大值0.999 6,即该电流曲线对应的温度响应曲线线性度最优,降温速率为31 ℃/min。此时电流曲线介于f(t2)曲线与f(t)曲线之间。

本研究通过非稳态过渡电流驱动机制,弥补了恒定电流与单一函数电流对应的温度响应曲线相比于线性降温曲线的冷量盈余与缺口,进而实现了微流体的线性降温。

为了获得其他线性降温速率下对应的电流驱动机制,可以通过改变最大降温时间tgen的方式改变冷量的输入,其中tgen为TEC工作电流自0逐步增至最佳工作电流4 A的时间。同样地,在不同降温时间下,通过改变非稳态过度电流的驱动机制并对温度响应曲线进行线性度分析即可实现不同速率的微流体线性降温过程,本研究实现了微流体在-19～26 ℃之间与24～42 ℃/min的线性降温且线性度均在0.998以上,线性降温电流波形与温度响应曲线如图10所示。由图10的仿真结果可知,随着tgen的增加,降温速率逐渐下降,获得线性降温对应的非稳态驱动电流逐渐由趋近于f(t2)波形变化至趋近于f(t)波形。值得注意的是,当tgen过低时,由于TEC存在最佳工作电流,制冷量有限,因此难以实现微流体更大速率的线性降温目标;由于微流控芯片底部的低温氮气也会对微流控芯片进行冷却,导致存在一个最低的线性降温速率。

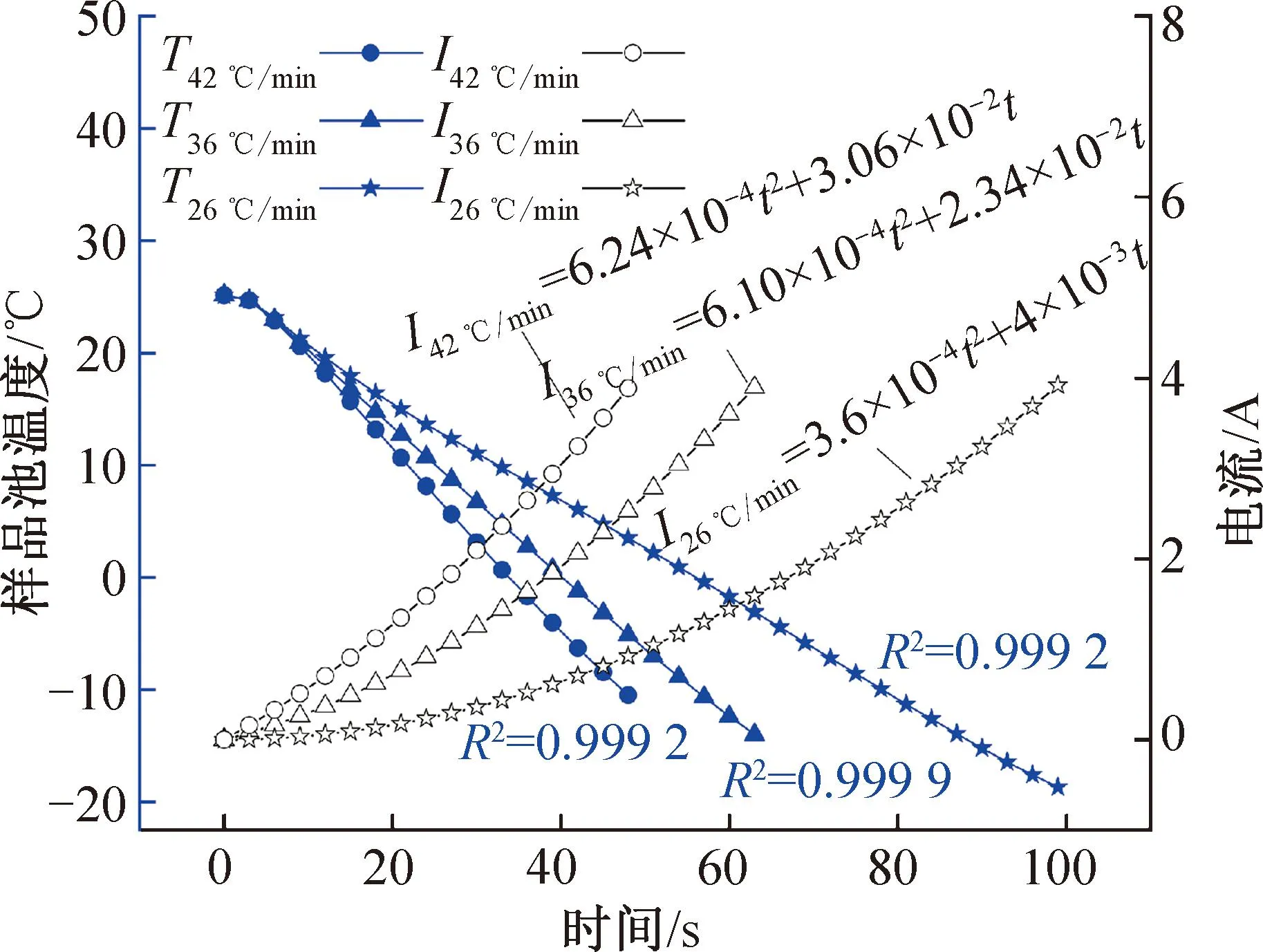
图10 线性降温电流波形与温度响应曲线

为进一步验证利用非稳态过渡电流驱动机制实现热电冷却微流体线性降温的准确性,利用图3所示实验系统进行实验验证。将仿真获取的降温速率分别为24、29、41 ℃/min的电流函数输入可编程直流电源,控制TEC的工作电流,实验过程中输入电流与实测电流如图11所示。

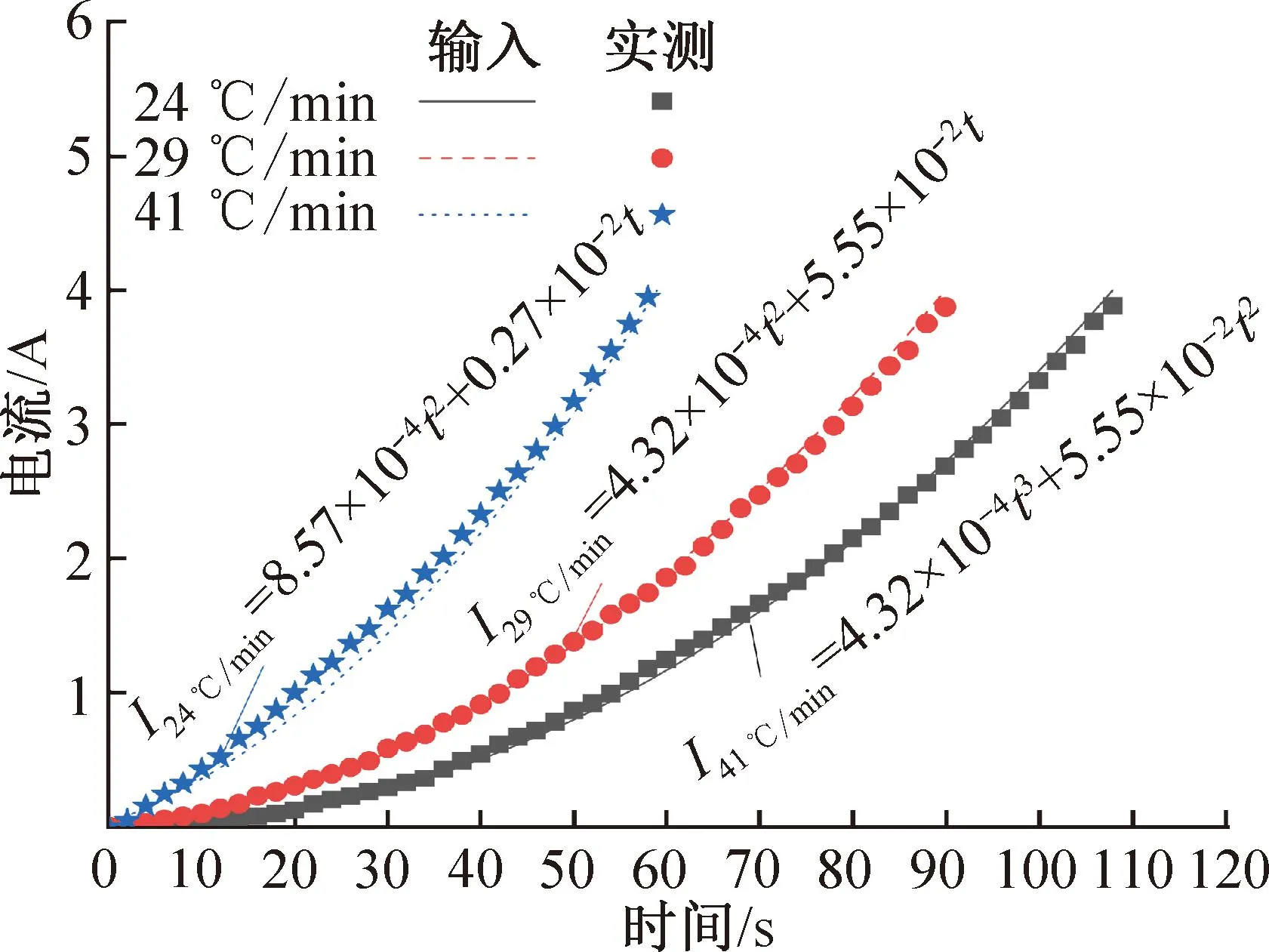
图11 实验电流输入值与实测值曲线

实验结果和仿真结果的对比如图12所示,由图可知,实验同样实现了热电冷却微流体的线性降温,与仿真结果吻合较好;其中,24、29、41 ℃/min降温速率对应的仿真线性降温过程的线性度分别为0.999 2、0.999 9、0.999 5,实验过程线性降温的线性度分别为0.998 1、0.998 9、0.999 2,略低于仿真结果,但仍符合实现微流体线性降温的要求。

图12 线性降温温度曲线

4 结论

本文设计了基于热电制冷的微流控芯片温度控制系统,通过仿真和实验研究了该温度控制系统的温度响应特性,通过非稳态过渡电流实现了电流、制冷量及微流体温度之间的线性耦合响应,实现了热电冷却微流体的线性降温。得到结论如下:

1)稳态电流驱动热电制冷器进行冷却降温的过程中,在TEC最佳工作电流4 A下,微流体样品池最低温度为-30.2 ℃。在0～300 s内,降温曲线的R2为0.598,难以实现线性降温的目标。引入非稳态过渡电流,可以显著提升微流体样品池降温过程的线性度。

2)对f(t0.5)、f(t)、f(t2)三种电流曲线进行了耦合获得了实现热电冷却微流体线性降温的电流驱动机制,最终实现了微流体在-19～26 ℃与24～42 ℃/min的线性降温,线性度在0.998 1以上。最后,对仿真获得的电流驱动机制进行实验验证,实验同样实现了热电冷却微流体的线性降温,与仿真结果吻合较好。

本文受中央高校基本科研业务费专项资金(JZ2021HGTB0093)资助。(The project was supported by the Fundamental Research Funds for the Central Universities (No. JZ2021HGTB0093).)