Turbo Message Passing Based Burst Interference Cancellation for Data Detection in Massive MIMO-OFDM Systems

Wenjun Jiang,Zhihao Ou,Xiaojun Yuan,Li Wang

National Key Laboratory of Wireless Communications,University of Electronic Science and Technology of China,Chengdu 611731,China

Abstract: This paper investigates the fundamental data detection problem with burst interference in massive multiple-input multiple-output orthogonal frequency division multiplexing(MIMO-OFDM)systems.In particular,burst interference may occur only on data symbols but not on pilot symbols,which means that interference information cannot be premeasured.To cancel the burst interference,we first revisit the uplink multi-user system and develop a matrixform system model,where the covariance pattern and the low-rank property of the interference matrix is discussed.Then,we propose a turbo message passing based burst interference cancellation (TMP-BIC) algorithm to solve the data detection problem,where the constellation information of target data is fully exploited to refine its estimate.Furthermore,in the TMP-BIC algorithm,we design one module to cope with the interference matrix by exploiting its lowrank property.Numerical results demonstrate that the proposed algorithm can effectively mitigate the adverse effects of burst interference and approach the interference-free bound.

Keywords: burst interference cancellation;data detection;massive multiple-input multiple-output(MIMO);message passing;orthogonal frequency division multiplexing(OFDM)

I.INTRODUCTION

Interference is one of the key factors that deteriorate the performance of wireless communications.In a cellular system,interference may exist throughout the whole frame or only on a few OFDM symbols.For the former,the development of interference cancellation technology has attracted extensive research interest in the past decade,and many effective approaches have been proposed [1].The impact of inter-cell interference(ICI)on multi-cell network systems has been investigated and analyzed in cases of inter-cell cooperation and non-cooperation [2],[3].In [4],an inter-symbol interference (ISI) suppression scheme employing the periodic signals for network MIMO-OFDM systems is proposed.Recently,the successive interference cancellation and alignment(SICA)scheme is proposed in the multi-user interference channel with partial unidirectional strong interference[5].

Different from the abovementioned interference scenarios,this paper focus on the scenario as shown in Figure 1,where the so-called burst interference only contaminates data symbols rather than pilot symbols in a transmission time interval (TTI).Burst interference is usually caused by unpredictable external interferers or other coexisting co-channel links.For instance,the refractive ratio of the atmosphere decreases rapidly with increasing altitude under certain weather conditions,which causes waves at the upper boundary of the atmosphere to be reflected back to the ground,known as the atmospheric ducting phenomenon [6],[7].Electromagnetic waves in atmospheric ducts propagate over the horizon with a much lower path loss than normal,which brings unexpected,significant and dynamic interferences to wireless communication systems.Another typical scenario is the coexistence of different communication links over the same frequency bands,where multiple transceivers communicate asynchronously nearby and are affected by interference from the other coexisting links[8].

Figure 1.The scenario where an OFDM frame suffers from burst interference in a few data symbols.

The lack of interference information makes burst interference cancellation a difficult task.In [9],the authors considered the strong impulse noise in the OFDM system and used the compressed sensing(CS)algorithm to realize the noise elimination by exploiting the sparsity of the time-domain impulse noise.The occurrence time of the impulse noise in [9] is much lower than one OFDM symbol.However,the duration of the burst interference considered in this paper lasts for one or even several OFDM symbols,and does not have usable sparsity in the time domain.In [8],the authors proposed a new burst interference suppression approach based on space-time processing(STP),where part of the conventional centralized pilot sequence is scattered and embedded into the transmitted data to capture the information of burst interference.However,the approach in [8] uses additional pilots resulting in a decrease of the data transmission rate,and the scattered pilots will be wasted when burst interference does not occur.For the burst interference scenario,a useful observation is that the power of the interfered symbol averaged over subcarriers is higher than that of interference-free symbols.Therefore,the location of the burst interference can be determined by energy detection[10].Nevertheless,since the pilot symbol phase may fail to measure the burst interference or collect any relevant helpful information,it is a great challenge for interference cancellation in the data detection phase.To tackle the above issues,we propose a message-passing-based algorithm for data detection and burst interference cancellation in massive MIMO-OFDM systems.The main contributions of this paper are summarized as follows:

• We first revisit the multi-user MIMO-OFDM systems under burst interference and establish a matrix-form system model to exploit the channel correlation over adjacent subcarriers.Based on the system model,we discuss the covariance pattern and the low-rank property of the interference matrix,where channel frequency selectivity leads to a few leaked singular values.

• To effectively detect the data,we propose a turbo message passing based burst interference cancellation(TMP-BIC)algorithm.The proposed algorithm consists of three modules named Modules A,B,and C.Particularly,Module A is a linear estimator that coarsely estimates data and interference by exploiting the covariance matrix of the interference.Module B refines the estimates of user symbols by exploiting the symbol constellation.For Module C,we design two different denoisers to further estimate the interference by exploiting the low-rank property,where the main difference between the two denoisers lies in the handling of the leaked singular values.These three modules are executed iteratively until convergence.

• We conduct extensive numerical simulations(under various modulation types,signal-to-noise ratio (SNR),and interference strengths) to evaluate the algorithm performance.Numerical results show that the TMP-BIC algorithm significantly outperforms the counterparts,and can approach the interference-free bound.

The remainder of this paper is organized as follows.The system model and the problem formulation are described in Section II.Section III presents the proposed TMP-BIC algorithm.Section IV shows the simulation results,and Section V concludes this paper.

II.SYSTEM MODEL

2.1 MIMO-OFDM System with Burst Interference

Consider a MIMO-OFDM uplink system with a base station (BS) servingNsingle-antenna users.The BS antenna is arranged in the form of aMx×My×E=Muniform planar array (UPA),whereE ∈{1,2}withE=1 representing antenna element with line(or circular)polarization andE=2 representing antenna pair with cross polarization.Besides,MxandMyrepresent the number of antennas(or antenna pairs)in the row and the column,respectively.Denote byKthe number of subcarriers for data transmission.Denote byPthe number of interferers and byTthe number of interfered data symbols.Both the user signal and the burst interference arrive at the BS through multipath fading channels.Assume that the channels remain unchanged during a TTI.Denote byhk,n ∈CMthe channel of usernon subcarrierk,and bythe channel of interfererpon subcarrierk.The channel model is expressed as[11,12]

whereϵn,l ∈CE(orϵp,l ∈CE) are the complexvalued channel coefficients of thel-th path of usern(or interfererp);⊗represents the Kronecker product;τn,l(orτp,l)is the path delay;Δfis the OFDM subcarrier spacing;θn,l(orϕn,l)is the azimuth(or elevation)angle of arrival;a(θ,ϕ)∈CMis the steering vector associated with the UPA arrangement,and is defined as

with

In(4),λdenotes the carrier wavelength,andddenotes the distance between two adjacent antennas.

Given channel models(1)-(4),the received signal on subcarrierkand interfered symboltis expressed as

whereHk=[hk,1,...,hk,N]∈CM×N,sk,t ∈CNdenotes the symbols of all users,and each symbol is constrained on a constellation setwhere theu-th element is the constellation pointrepresents the data of all interferers,andnk,t ∈CMis an additive white Gaussian noise(AWGN)with the element-wise variance of.Without loss of generality,we assume the unit average power ofsk,tand.Note that the unit power assumption is satisfied by normalizingsk,tand combining the symbol power with the channel response of the user (or the interferer).Since bothin (5) are unknown,we express the burst interference on subcarrierkof symboltasThen,the system model(5)is rewritten as

The frequency-domain channel varies slowly over adjacent subcarriers,and we divideKcontinuous subcarriers intoQblocks of lengthK/Q.Since each block is processed separately using the same operations,we consider the model on one block as follows with some abuse of notation.Denote byxk,t=Hksk,t ∈CM×1the received signal of users.The received signal at interfered symboltis given by the matrix form as

whereYt=[y1,t,...,yK/Q,t]∈CM×K/Q,Xt=[x1,t,...,xK/Q,t]∈CM×K/Q,Lt=[l1,t,...,lK/Q,t]∈CM×K/Q,andNt=[n1,t,...,nK/Q,t]∈CM×K/Q.Further,the signals of one block on all interfered symbolst=1,...,Tare combined into a matrix as

whereY=[Y1,...,YT]∈CM×Jwith column numberJ=KT/Q,X=[X1,...,XT]∈CM×J,L=[L1,...,LT]∈CM×J,andN=[N1,...,NT]∈CM×J.

2.2 Propeties of Interference

This paper focuses on a UPA at the BS,which leads to a specific pattern in the interference covariance matrix.More specifically,the covariance matrix ofLis expressed as

To explicitly see the pattern ofCL,Figure 2 shows the normalizedCLcorresponding to the UPA arranged inMx=4 rows andMy=8 columns with crosspolarizationE=2.We see thatCLtends to be a block diagonal matrix with 8 diagonal blocks of size 8×8.This block-diagonal structure matches the UPA arrangement withM2=8 columns andM1E=8 antennas in each column.It is worth noting that in Figure 2 some triangular areas on the diagonal appear with low correlation,which is caused by the large distance between the tail of the current column and the head of the next column.

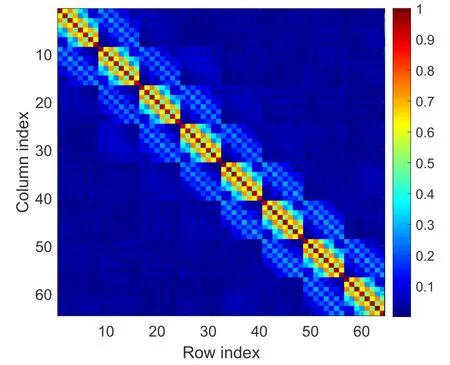
Figure 2.An example of the normalized covariance matrix of interference,where the antenna array is arranged in 4 rows and 8 columns with cross polarization. Channel coefficients are generated by the quadriga toolbox using the CDL-B channel model[10,Table 7.7.1-2].

Another aspect is thatLexhibits a low-rank property since the number of interferencePis usually much smaller than the number of the BS antennaMin the massive MIMO scenario[13,14].Specifically,if the channel within a block is flat-fading (i.e.,the channelsare identical on all subcarriers in a block,denoted asHI,) the interference matrix can be expressed asThen,we obtain that the rank ofLequals the rank ofHI ∈CM×P,i.e.,the number of interferencePwithP ＜M.In practice,since the channel frequency selectivity leads to variation between adjacent subcarriers,Lhas some leaked singular values as shown in Figure 3.This leakage issue needs to be appropriately addressed in interference cancellation,as detailed later in Section III.Note that a larger block numberQreduces the subcarrier number in each block,thus making the frequency-domain channel of one block more flat with a lower singular leakage.However,with the increase ofQ,the column numberJ=KT/QofLdecreases,which leads to fewer observations inL.As such,by adjustingQ,there is a trade-off between the degree of singular leakage and the number of observations.

Figure 3.The normalized singular values of interference matrix Lq with the number of interferers P=8 and the number of receiving antennas M=64.

2.3 Problem Formulation

We now describe the considered problem as follows.Based on the model(8),our goal is to suppress the interferenceLand detect data{sk,t}upon the received signalsYby exploiting the low-rank property ofLand the constellation information{cu}of{sk,t}.Note that the user channelHkcan be estimated on the pilot symbols without burst interference,so allHkis assumed to be perfectly known in this paper.1The channelof interference is unknown.In the next section,we propose an iterative message-passing based burst interference cancellation algorithm (TMP-BIC)to suppress the interference and detect the target data from the received signal.

III.TMP-BIC ALGORITHM

3.1 Algorithm Framework

The diagram of the proposed TMP-BIC algorithm is shown in Figure 4,which involves three modules,and the burst interferenceLis to be estimated for cancellation in TMP-BIC.Specifically,Module A provides coarse linear estimates of{sk,t}andLbased on the noisy measurementYin(8).Module B is used to refine{sk,t}by exploiting the constellation information.Module C is to estimateLby exploiting the low-rank property.These three modules are executed iteratively to refine the estimates of{sk,t}andLuntil a stopping condition is met.In what follows,variable superscripts denote different types of variable messages.SubscriptsA,B,andCare used to distinguish estimates from different modules.As shown in Figure 4,is the input estimate ofsk,tat Module A,where superscript“pri”represents the prior(input)message;is the output estimate ofsk,tfrom Module A,where superscript“ext”represents extrinsic message.As for estimation variance,e.g.,is the extrinsic variance ofSat Module B.Similar notations apply to the variableL.

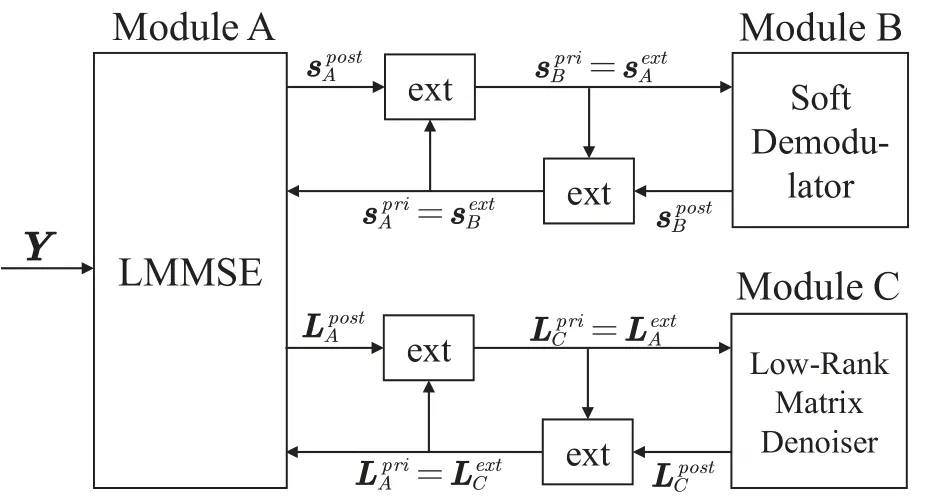
Figure 4.The diagram of the TMP-BIC algorithm.

3.2 Module A:Linear Estimator

We now present the details of Module A,where the linear minimum mean square error(LMMSE)estimator is used to provide coarse estimates of{sk,t}andL.The posterior estimates ofsk,tandlk,tare given by

where tr(·)represents trace operator.Note that a commonly used approximation ofCLis to treat it as a diagonal matrix [15].This diagonal matrix approximation ignores the correlation of the interference elements at different received antennas,and is not accurate when the antenna array is a UPA.To obtain a better estimate,we replace it with the covariance pattern given in Section 2.2.

Then,we average the posterior variances ofsk,tandlk,tin one block as

From the turbo message passing [16],the extrinsic messages ofsk,tandLin Module A are respectively given by

3.3 Module B:Soft Demodulator

In Module B,the constellation information{cu}of target symbol{sk,t}is used to refine the input=where the operation is similar to a soft demodulator.By utilizing the constellation in each iteration,the interference contained in the symbol estimates is gradually eliminated.We first calculate the posterior probability oftaking theu-th constellation point as

where|·|denotes the magnitude of a complex variable.Givenwe obtain the posterior mean and variance of each element as

Similar to Module A,we average the posterior variances in each block as

Then,the extrinsic messages ofsk,tin Module B are given by

3.4 Module C:Low-Rank Matrix Denoiser

Module C further estimates the low-rank matrixLfrom the input estimate.We design two denoisers in the following.

3.4.1 Approach 1: Best Rank-rDenoiser

We ignore the small leaked singular values ofL,and regardLas an ideal rank-rmatrix.The rankris estimated by adopting the minimum description length(MDL) algorithm [17,eq.(17)] over.Next,we adopt a best rank-rdenoiser[18],which is defined by the following optimization problem:

where||·||Fandrank(·)denote the Frobenius norm and the rank of a matrix,respectively.Let the singular value decomposition (SVD) ofUΣVH,whereU∈CM×M,V∈CJ×J,andΣ=diag(σ1,σ2,...,σmin(M,J))∈RM×Jis a diagonal matrix with the singular valuesσiarranged in the descending order.The posterior mean ofLis the solution to the above problem as

whereDL(·) denotes the denoiser employed in Module C,andΣr ∈RM×Jis a diagonal matrix with the firstrdiagonal elements beingσ1,...,σrand the others being zeros.

3.4.2 Approach 2: Optimal Shrinker

The best rank-rdenoiser sets all leaked singular values to be zeros,which loses some useful information.To achieve better performance,we consider a more efficient denoiser in[19]to deal with the leaked singular values,termed as optimal shrinker(nuclear norm).As shown in Figure 5,the firstrsingular values estimated by the optimal shrinker are almost consistent with the real values,and the leaked singular values are selectively retained.The detailed operation of the optimal shrinker is as follows.

Figure 5.The normalized singular values of the interference matrix L with the number of interferers P=8 and the number of antennas M=64.

withβ=M/J.Then,the singular value is again shrunk as

Then,the posterior mean ofLis given by

whereΣopt=diag(η(σ1),...,η(σmin(M,J)))∈RM×J.

3.4.3 Extrinsic Message Computation

where the combination parameters are given by

where div(·)denotes the matrix divergence,and〈·,·〉denotes the inner product of two matrices.The computation of the extrinsic meanensures that the output estimation error-Lis uncorrelated with the input estimation error-L,which is the key for the iteration convergence.For more details,see[20,Sec.III].Then,considering the stability of the algorithm,the extrinsic variance is obtained by a robust approach[21,Sec.V-D]as

3.5 Overall Algorithm

The overall algorithm is summarized in Algorithm 1.Compared with the turbo-type message passing(TMP)algorithm in[21],the proposed TMP-BIC has necessary modifications in each module.In Module A,TMP-BIC replaces the diagonal approximation with the covariance matrixCL.Module B replaces the sparse matrix estimator with a soft demodulator which obtains the symbol-wise posterior probability.In Module C,we propose the optimal shrinker to deal with leaked singular values.

We now analyse the computational complexity.Module A mainly involves matrix inversion and matrix multiplication with complexityO(KM3) andO(KTNM(M+N)),respectively.Module B involves entry-by-entry calculation with complexityO(KTNU).For Module C,the complexity is dominated by the SVD ofwith complexityO(KM2).Besides,the number of non-zero singular values ofLis much less than the number of antennasMand is about twice the number of interferersP,so the complexity of SVD can be reduced toO(KMP).

IV.NUMERICAL RESULTS

In this section,we evaluate the detection performance of the TMP-BIC algorithm.Channel coefficients are generated by the Quadriga toolbox in the Urban Macro(UMa)scenario[10,Table 7.5-6].For a robustCLin(11),we computeCLby averaging over 104independent experiments,whereθp,l,∀p,lrandomly takes the values within [-π,π],ψp,l,∀p,lrandomly takes the values within[-π/2,π/2].Note that the channels for the computation ofCLand the simulations are generated independently.Unless otherwise specified,considerN=8 target users andM=64 receiver antennas,where the antenna array is arranged in 4 rows and 8 columns with cross-polarization.16 QAM constellation is adopted.The number of interferers isP=5 with the interference-to-noise ratio(INR)being 10 dB.The number of interfered symbols isT=2.The number of subcarriers isK=144,which is divided intoQ=3 blocks.The baselines are as follows:

• LMMSE: The burst interference is treated as an AWGN,and the LMMSE algorithm is used for the data detection[22].

• TMP: We modified the TMP algorithm in [21],where the sparse matrix estimation module is replaced by the soft demodulator in[23].

• Interference-free: We use the case of no burst interferences as a lower bound,and corresponding data detection is performed by LMMSE.

In Figure 6,the three blue curves represent the BER performances of TMP-BIC and TMP as a function of the iteration number,and the three orange curves represent the corresponding running time.The simulation platform is a Dell Optiplex 7090 Desktop with an i7-11700/2.50 GHz Intel-Core CPU and a 32 GB RAM.We see that compared to the TMP algorithm,the computational complexity of the TMP-BIC algorithm is nearly 30% higher.On the other hand,the TMP-BIC algorithm,especially with the approach 2,significantly outperforms the TMP algorithm in the BER performance by an order of magnitude.

Figure 6.Average BER(or running time)against the number of iteration. SNR=4 dB.

Figure 7 shows average BER versus SNR under different modulation types,where the iteration number of the message-passing algorithms is 40.It is seen that TMP-BIC approaches achieve considerable performance gain over the baselines.For example,compared with TMP,TMP-BIC(approaches 1 and 2)achieve SNR gains of 1 dB and 5 dB under QPSK at BER=0.01,respectively.The trends under 16 QAM and 64 QAM are similar.Besides,we observe that the gap between TMP-BIC and the lower bound increases as the modulation order increases.This is because in high-order modulation,the symbol correction capability at the soft demodulator is reduced,which meanwhile increases the power of detection error seen by the low-rank denoiser,and thus affects the interference suppression.Furthermore,we consider that the correlation of the interference signal between different antennas is ignored by the BS with TMP-BIC(approach 2),i.e.,CLis approximated as a diagonal matrix by setting its off-diagonal elements to be zeros.In this case,there is a performance loss within 1 dB.

Figure 7.Average BER versus SNR under different modulation types. Left: QPSK;Middle: 16QAM;Right: 64QAM.

Figure 8 shows the BER performances under different INRs,where we set INR=5 dB and INR=15 dB in the left and right sub-plots,respectively.The trends on the two sub-plots are similar.The TMP-BIC algorithm outperforms the baseline.When the INR increases,TMP-BIC (approach 2) exhibits a greater performance superiority over TMP-BIC(approach 1),which is because TMP-BIC (approach 2) better handles the singular value leakage.

Figure 8.Average BER versus SNR with INR=5 dB and INR=15 dB in the left and right plots,respectively.

Figure 9 shows average BER versus SNR under different numbers of receiver antennas and interferers,where TMP-BIC (approach 2) is adopted with 20 iterations.We see that the BER performance decreases as the number of interferences increases.More importantly,we see that the increase of the receiver antenna number leads to a performance improvement.For example,the SNR requirement for BER=0.01 andP=2 atM=32 is 5 dB higher than that atM=64.This is because an increase in the number of antennas provides higher diversity gain for the LMMSE estimator and contributes to a lower ratio of theL’s rank to its row number for the low-rank denoiser.

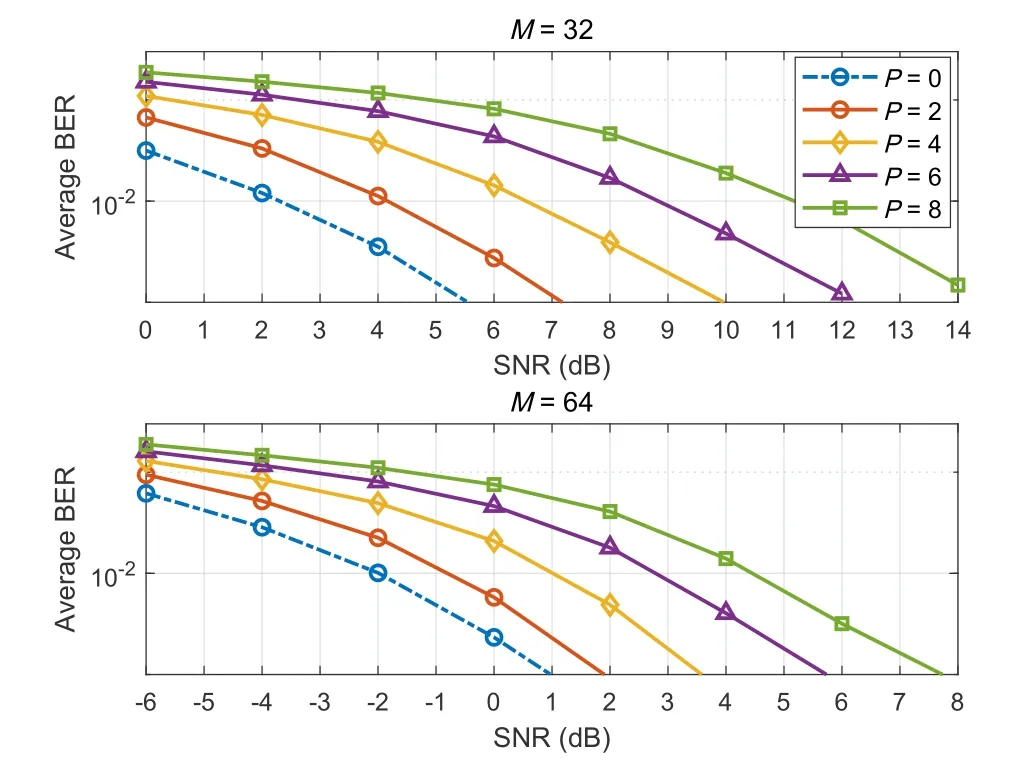
Figure 9.Average BER versus SNR under different numbers of receiver antennas and interferers. Top: M=32;Bottom: M=64.

Figure 10 shows average BER versus SNR under different numbers of interfered symbolsTand blocksQ,where TMP-BIC (approach 2) is adopted with 20 iterations.The performance achieves considerable gains with the increase in the number of interfered symbols,e.g,atQ=3,the SNR requirement for BER=0.01 decreases by 1.5 dB whenTincreases from 2 to 8.This is because the increase ofTdirectly leads to the increase of column numberJ=KT/QofL,which improves the performance of low-rank denoiser[24].We now consider how block numberQaffects the detection performance.Note that a smallerQleads to a largerJ,but makes the leaked singular values bigger.Under this trade-off,we see that the performance difference for differentQinT=4 and 8 is contrary to that inT=2.This result reveals that whenTis relatively large,e.g,T=4 and 8 in Figure 10,we can increaseQto ensure small leaked singular values.However,whenTis relatively small,e.g,T=2,we need to reduceQto ensure a sufficiently largeJso that the interference can be suppressed effectively.

Figure 10.Average BER versus SNR under different numbers of interfered symbols and blocks.

V.CONCLUSION

In this paper,we studied the data detection problem for the multi-user MIMO-OFDM system with burst interference.The received signals on adjacent subcarriers were combined into a block to construct the matrix-form system model.Based on the system model,we developed the TMP-BIC algorithm to cancel the burst interference,which effectively exploits the low-rank property of the interference matrix and the constellation information of the user symbol.Besides,the structure of the receiving antenna array was used to obtain the interference covariance matrix for the LMMSE module of TMP-BIC.The numerical results demonstrate that the TMP-BIC algorithm significantly outperforms the baselines and can approach the interference-free bound.

ACKNOWLEDGEMENT

This work was supported by the National Key Laboratory of Wireless Communications Foundation,China(IFN20230204).

NOTES

1When the burst interference exists in the pilot symbol,how to achieve a high-accuracy channel estimation is an interesting topic,but a detailed discussion on this topic is beyond the scope of this paper.