基于改进VMD和HP的滚动轴承故障诊断方法
吕品德,齐明思,时彦浩
(中北大学机械工程学院,山西 太原 030051)
滚动轴承是机械设备的重要零部件,其故障情况直接影响设备的正常运行。因此研究滚动轴承的故障检测方法具有十分重要的意义[1]。变分模态分解(variational mode decomposition,VMD)可以实现在分解模态的同时提取特征,具有较强的泛化能力和鲁棒性[2],但是依靠经验设置惩罚因子和分解层数会影响信号分解效果。张杰等[3]利用蝙蝠算法对VMD参数进行了优化,使其能够对振动信号进行自适应分解。熵作为一种特征提取方法,能够有效获取信号的规律性和微小变化,因而被广泛应用于故障诊断中[4]。王泽等[5]利用多尺度排列熵(multiscale permutation entropy,MPE)相关理论对滚动轴承进行了特征提取。
针对滚动轴承振动信号非线性、非平稳性以及特征难以提取导致分类准确率低等问题,本文提出了参数优化的VMD-MPE和层次原型(hierarchical prototype,HP)相融合的滚动轴承故障诊断方法,并通过实验验证其有效性。
1 VMD和鹈鹕优化算法
1.1 VMD
VMD是一种新的信号分解方法,它可将非平稳信号分解为不同时间尺度的平稳信号[6]。其目标是将输入信号f分解成具有G个中心频率wg的本征模态函数ug(t),其中g=1,2,…,G。具体步骤为:分解输入信号f,对每个模态函数的中心频率初始化,通过计算解调信号梯度的平方范数来估计每个模态分量的带宽。约束变分模型的表达式为:
(1)
其中:
{uG(t)}={u1(t),…,ug(t)}
{wG}={w1,…,wg}
式中:t为时间,Au是把每个模态分量调制到所相对应的基频带中得到的解析信号,∂t为对时间t的偏导。
为了求得约束变分问题的最优解,引入惩罚因子α和拉格朗日乘子λ建立不受约束的方程,得到增广的拉格朗日函数:
(2)
式中:L({ug(t)},{wg},λ)为增广的拉格朗日函数,f(t)为原始信号。

(3)
(4)

用式(2)更新λ(w)可得:
(5)
式中:ψ为时间常数。
反复执行上述迭代的每一步,直至满足迭代停止条件:
(6)
式中:ε为判别精度,ε>0。
1.2 鹈鹕优化算法
鹈鹕优化算法(pelican optimization algorithm,POA)是2022年由Trojovsk等[7]提出的一种种群智能优化算法。其主要步骤如下:
1)初始化参数。鹈鹕种群数量规模为m,最大迭代次数为B,随机在[0,1]上生成鹈鹕位置。
2)第1阶段(探索阶段)为向猎物移动时,鹈鹕位置为:
(7)

3)第2阶段(开采阶段)为鹈鹕在水面上飞翔时,鹈鹕位置为:
(8)

4)位置更新。
(9)

5)重复上述步骤,直到获得最优值。
1.3 参数优化和特征提取
利用POA对VMD参数组合[α,G]进行优化,并对原信号进行分解得到层IMF,选择样本熵最小的IMF分量作为特征向量,同时对其进行包络谱分析,其流程图如图1所示。

图1 参数优化和特征提取流程图
1.4 仿真信号分析
拟采用如下模型来模拟滚动轴承内圈故障产生的振动信号[8]:
(10)
式中:s(t)为添加了高斯白噪声的振动信号;Vi和g(t-iT1)均为振动信号;m(t)为周期性的信号冲击;n(t)为高斯白噪声,其信噪比取-13 dB;T1为周期;g(t)为随指数衰减的余弦冲击信号;V0为幅值,取值0.3;fr为转频,取值30;Q为衰减系数,取值700;fn为共振频率,取值4 000 Hz。
在仿真试验中,设置采样频率为16 kHz、采样时间为0.25 s,冲击与仿真信号的波形与频谱如图2所示。

图2 冲击与仿真信号的波形与频谱
在参数寻优过程中,根据表1中的相关参数,在POA每次迭代更新后,选择IMF最小样本熵值作为最优适应度函数值。图3所示为POA寻优曲线。

表1 POA相关参数设置

图3 POA寻优曲线
由图3可知,各IMF的样本熵值随着迭代次数的增加不断减小。从第27代到迭代结束一直保持最小样本熵值0.419 8。故此时最优参数组合为[α,G]=[2 823,4],同时更新VMD中相关参数并对原信号进行分解。图4为分解后的仿真信号波形和频谱。

图4 POA-VMD分解后的仿真信号波形和频谱
由表2得,IMF3样本熵的值最小,且IMF3含有频带中心为4 000 Hz的共振频带,杂质信号也较少,故选用IMF3。对其进行包络谱分析,结果如图5所示。在IMF3中,出现明显的特征频率fi以及其倍频。因此,通过对VMD的参数寻优和对仿真信号的分解,可以有效地获取滚动轴承的故障特征信息。

表2 4个模态分量的样本熵

图5 IMF的包络谱
2 多尺度排列熵(MPE)
2.1 多尺度排列熵的原理
多尺度排列熵灵敏度高,已经可以从多个尺度上计算测量时间序列的复杂度,因此广泛应用于机械设备检测中。多尺度排列熵原理的计算和推导过程如下:
对长度为Z的时间序列X(X={x1,xx,…,xZ})进行粗粒化,若尺度因子s取值为1,则原始序列和处理后序列相等同,即:
(11)
式中:ys,j1为多尺度时间序列,j1为随机变量,[Z/s]表示取整数。
对ys,j1进行时间重构可得:
Ys,a={ys,a,ys,a+ξ,…,ys,a+(m-1)ξ}
(12)
式中:m为嵌入维数;ξ为延迟因子;对于Ys,a,a表示第a个重构分量;Ys,a是对ys,j1进行时间重构后得到的结果。
将Ys,a升序排列,对任意h都有唯一符号序列S(r)={a1,a2,…,am},其中r=1,2,…,R1,且R1≤m!,计算每种符号序列出现的概率Pr。
经上述推导,MPE定义式为:
(13)
式中:Hp(m)为排列熵值。
由式(13)可知,Hp(m)最大值为ln(m!),将Hp(m)进行归一化处理可得:
hp(m)=Hp(m)/ln(m!)
(14)
式中:hp(m)是Hp(m)进行归一化处理后的结果。
2.2 技术路线与流程图
基于改进VMD和HP的滚动轴承故障诊断方法的技术路线和流程如图6所示,其详细步骤如下:1)采集滚动轴承振动信号;2)用POA优化VMD的惩罚因子和分解层数;3)通过改进VMD对信号进行分解,选择样本熵最小的敏感IMF分量;4)利用MPE计算所得到的各敏感IMF熵值,进而得到特征向量;5)将特征向量输入到HP中进行故障识别;6)对HP与KNN、SVM、DT、RF、DA进行比较。
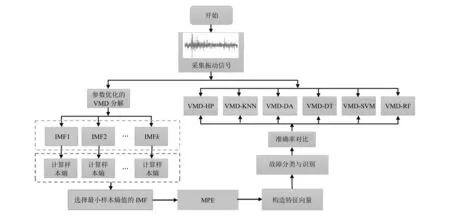
图6 技术路线与流程图
3 HP


图7 HP中第i个原型层次类型结构图
3.1 HP的学习阶段
对所有的样本进行标准化可得:
(15)
(16)

(17)

(18)

(19)
(20)

(21)
3.2 HP的测试阶段
对于没有标签的样本xK,将其导入每个层次以获得一系列分数λi(xK):
λi(xK)=e-‖p-xK‖2
(22)
即计算各个原型与测试样本的相似度λi(xK),进而找出最大相似度的原型代表类别,然后将预测标签与实际标签进行比较,以测试模型的性能[10]。
4 滚动轴承故障诊断
采用滚动轴承故障实验平台所采集的振动信号进行故障诊断实验,装置如图8所示。测试的滚动轴承型号为LDKUER204。在电机转速为1 500 r/min、加速度传感器采样频率为12.8 kHz状态下采集振动信号。实验台分别设置了4种状态:滚子故障、外圈故障、内圈故障和正常,所述几种故障状态均由人工通过线切割开槽进行添加。

图8 实验装置图
在除正常外的其他3种故障状态下设置5种载荷,分别为150、300、450、600、750 kg,在12.8 kHz采样频率下,选用内圈、外圈、滚子分别在负载150 kg和300 kg下的故障实验数据以及无故障实验数据共7种类型,见表3。每种故障类型选取50组样本,每个样本有1 024个数据点。其中NO为无故障,IF为内圈故障,OF为外圈故障,BF为滚子故障。

表3 不同状态的类别标签
4.1 特征提取
采用POA-VMD方法对全部样本信号进行合理分解并计算所得IMF样本熵值。利用MPE再次进行特征提取,如图9所示。在同一尺度下,不同信号的敏感IMF分量的MPE熵值都能很好地表征出来。郑近德等[11]通过仿真发现,当尺度因子s=11、嵌入维数m=6、时间延迟τ=1时,能够有效提取出滚动轴承信号中的特征信息。本文借鉴其实验参数,依次用MPE计算获得的敏感IMF分量的熵值,最终得到了一个350行11列的由MPE熵值组成的特征向量矩阵。

图9 多尺度排列熵提取滚动轴承的特征向量
4.2 故障分类与诊断
将特征向量矩阵数据按照训练集和测试集8∶2进行随机分配并输入到HP中,绘制诊断结果混淆矩阵,如图10所示。

图10 故障诊断结果混淆矩阵示意图
这里将VMD+MPE-HP和支持向量机(SVM)、决策树(DT)、K最近邻(KNN)、随机森林(RF)以及线性判别(DA)分类器进行对比实验。实验中每种方法的数据都与HP分类器相同。分别运行5次并打乱训练集,整理后的结果见表4。由表可知HP的分类精度最高,分类结果的标准差与其他各分类结果相比最小,证明其整体分类效果优于其他模型,且具有较好的稳定性。

表4 不同分类方法的分类结果
5 结论
本文提出一种基于改进VMD和HP的滚动轴承故障诊断方法,通过实验表明:1)通过参数优化的VMD能够使振动信号更好地自适应分解;2)将改进VMD和MPE相融合,将振动信号粗粒化处理,再结合多尺度相关理论,能够更全面地提取振动信号的故障特征;3)基于改进VMD和HP的滚动轴承故障诊断方法有着较高的分类准确率。

