一道2023年江苏高考物理试题的深入探讨

邵 云

(南京晓庄学院电子工程学院,江苏 南京 211171)

1 问题的缘由

2023年江苏高考物理试卷第10题(选择题)是一道很有意义的题目,该题的题设如下.

例题.达·芬奇的手稿中描述了这样一个实验:一个罐子在空中沿水平直线向右做匀加速直线运动,沿途连续漏出沙子．若不计空气阻力,则图1中能反映空中沙子排列的几何图形是[1]

图1 高考物理试卷第10题(选择题)的题图

达·芬奇提出的问题看似平凡实则蕴含着深刻的物理思想．从考生的角度看,选择正确的答案(D)并不是十分艰难,但是从教学研究的角度看,其实教师也未必能够把其中的物理情境交代得清楚明白,即未必能够把握住其中内涵的深刻物理思想．[2,3]如果罐子在空中沿水平直线做匀速运动(或者静止),那么沙子在空中的排列形状应如选项(A)所示,为一竖直直线,这正是伽利略惯性实验揭示的原理．伽利略把一个苹果挂在匀速运动的船桅顶上,苹果落下后一定还在船桅的正下方;现设想把沙罐挂在船桅顶上,让沙罐里的沙子连续漏下,则不论从船上看还是从岸上看,它们必定成一条与船桅杆平行的直线;然而本题达·芬奇提出罐子在空中沿水平方向向右做匀加速直线运动,选项(A)倒是很容易排除,但是(B)(C)(D)3个选项却不那么容易判断,且十分具有迷惑性．

2 在地面静止参考系中求解

2.1 空间轨迹法

如图2所示,设罐子在t=0时刻位于坐标原点O处,从静止开始以恒定的加速度a沿x轴正方向运动;在tn时刻第n颗沙子Pn离开罐子,它在t(>tn)时刻到达图2中位置处．

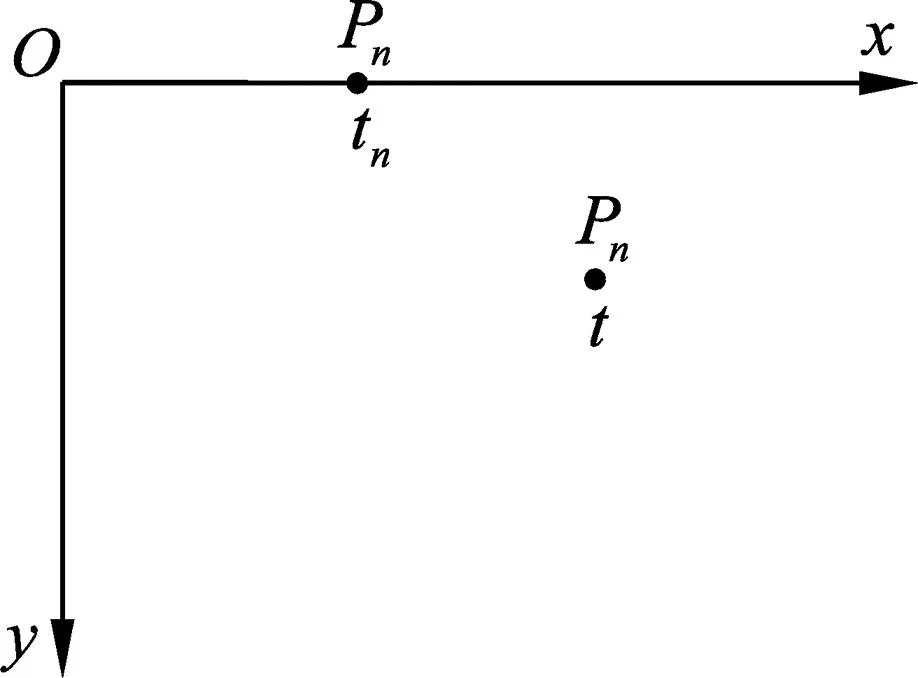
图2 第n颗沙子Pn的位置示意图

根据题意及以上设置可得,tn时刻沙子Pn的x、y坐标分别为

(1)

yn(tn)=0.

(2)

t时刻沙子Pn的x、y坐标则分别为

(3)

(4)

其中g为重力加速度．联立式(3)(4),消去tn后即得

(5)

式(5)即为第n颗沙子Pn的坐标xn、yn所满足的方程．式(5)显然与沙子的序数n无关,即方程式

(6)

能够适用于所有t时刻之前漏出的沙子．虽然每颗沙子下落的时间t-tn不同,但是方程式(6)只与时刻t有关,并且所有在空中下落的沙子同处t时刻,于是式(6)即为一直线方程．这就意味着,所有之前漏出的沙子在t时刻均排列在该直线上,如图3所示．因此(D)是正确的选项．

2.2 相对空间方向

任取t时刻前的两颗沙子A、B,设它们离开罐子的时刻分别为tA、tB,且tA

vA(t)=atAi+g(t-tA)j.

(7)

vB(t)=atBi+g(t-tB)j.

(8)

则在t时刻,沙子A相对于沙子B的相对速度矢量为

vAB(t)=vA(t)-vB(t)=a(tA-tB)i+

g(tB-tA)j=(gj-ai)(tB-tA).

(9)

鉴于A、B两颗下落的沙子之间的时间差tB-tA在下落过程中保持不变,因此式(9)所表达的是一个常矢量,即任何两颗离开罐子的沙子,彼此之间相对都在做匀速直线运动,并且前一颗沙子相对于后一颗沙子的相对速度均统一沿常矢量gj-ai的方向.这就表明:所有漏出的沙子均排列在沿gj-ai方向的同一条直线上,彼此间相对做速度大小不等的匀速直线运动,呈现出与多个小球在同一地点依次自由下落相似的相对运动图像．易见该直线在Oxy坐标系中的斜率为-g/a,这与上一种解法中所获得的直线方程式(6)相一致．该直线如图4所示．

图4 A、B等沙子及罐子的位置及相对方位示意图

3 参考系变换

罐子在x轴正方向做匀加速直线运动,因此罐子是一个直线加速非惯性参考系．在非惯性参考系中,人们通常是通过引入惯性力来使牛顿第二定律依然能够成立．[4]在罐子参考系中,设每一颗沙子的质量均为m,则其惯性力为-ma,与重力mg相叠加,即得沙子所受等效重力也即视重力为

mg视=m(g-a).

(10)

视重力加速度为

g视=g-a.

(11)

式(10)(11)便是在罐子参考系中沙子所感受到的重力和重力加速度．

如图5所示,沙子相对于罐子将沿g视的方向依次做自静止开始的“自由落体”运动．很显然,从固联在罐子上的x′O′y′坐标系(即罐子参考系)来看,诸沙子均在同一条直线上运动,该直线在x′O′y′坐标系中的斜率为-g/a．这些观察结果与地面静止参考系中所观察到的结果完全一致.

容易证明图4和图5中A、B两颗沙子间的相对运动速度是相等的,即有

vAB′(t)=vAB(t).

(12)

这就是说,尽管所有沙子的速度均与参考系有关,但是各沙子彼此之间的相对运动(包括相对速度、相对位移等)却与参考系无关.这其实是经典的伽利略时空变换、速度变换等的必然结果．由于各沙子在空间的位置相对分布仅与彼此间的相对运动有关,因此各沙子在空间的位置相对分布就与参考系无关了,换言之,在不同的参考系中,无论惯性系与非惯性系,对于沙子排列形状的观察结果都应该是相同的、等价的．

4 比较“类”判断

罐子在水平方向上的运动,粗看起来可以分为匀速直线运动(包括静止)、匀加速直线运动、变加速直线运动这3类;但是细看起来,匀速直线运动(包括静止)可以被看作加速度为0的匀加速直线运动;于是,罐子在水平方向上的运动便只有两类了,即匀加速直线运动和变加速直线运动．

既然罐子在做匀速运动(包括静止)时,沙子在空中的排列形状是一条竖直直线,即选(A),那么当罐子向右做匀加速直线运动时,沙子在空中的排列形状也应是一条直线,只是该直线是倾斜的,形如图1(D),即选(D)．当然,其中也有沙子在水平方向和竖直方向先后做匀加速度运动的考量——水平和竖直方向存在着某种对称性．不难料想,当罐子向右做匀减速直线运动时,沙子在空中的排列形状将是一条2、4象限的直线．

至此,图1(B)、图1(C)就容易理解了．图1(C)所表达的应是罐子向右做变加速(加速度的大小a不断增加)直线运动的情形;而图1(B)所表达的则是罐子向右做变减速(减速度的大小a不断增加)直线运动的情形．这些道理从第3节的罐子参考系中不难理解．以罐子向右的加速度大小a=kt(k为常量)为例,可以求得t时刻诸沙子坐标x、y所满足的方程为

(13)

图6 在t=10 s时t≤10 s内从a=t m/s2的罐子中

5 总结

本文介绍了求解2023年江苏高考物理试卷第10题(选择题)的4种方法,其中的第1种解法比较常规——直接在地面静止参考系中求出在t时刻空中的任意沙子坐标(xn,yn)均需满足的、统一的直线方程式(6),由此获得正确的选项(D)．第2种解法则是通过论证地面静止参考系中任意两颗沙子之间的相对速度[即上文vAB(t)]均沿同一个方向(即常矢量gj-ai的方向),来证明所有的沙子均在同一条直线上,从而获得正确的选项(D)．该解法的思路十分简单,并且过程简洁,但是需要一定的抽象思维能力．第3种解法更加简便——直接将罐子参考系中观察到的沙子排列在同一直线上的图像移植到地面静止参考系中即可．但是该解法需要充分地掌握伽利略变换的知识,并且能够充分地理解其推论:质点系内各质点彼此之间的相对运动(包括相对速度、相对位移等)与参考系无关,因此各质点在空间的相对分布状况便与参考系无关．第4种解法则需要领悟罐子的匀速直线运动(包括静止)和匀加速直线运动,在本问题中其实属于同一大类——前者只是后者的一个特例．因此它们的空间沙子排列形状也应该属于同一类型,既然前者沙子的排列形状是一条竖直直线,那么后者沙子的排列形状便是一条斜直线．另一大类是变加速或者变减速运动,其中罐子加速度越来越大的空间沙子排列形状对应于图1(C),而罐子减速度越来越大的情形则对应于图1(B)．倘若将以上罐子的运动情况颠倒,例如将匀加速变成匀减速,或者越来越大变成越来越小,则会获得另外3个图像,这里不再赘述．

感谢:对于本文所研究的试题,江苏省南通市海门实验学校姜兵老师从几何特征上给出了综合性的评价,即沙子排列曲线局部的空间斜率倒数即代表罐子的加速度,颇具启发性,在此鸣谢．