非均匀伴流中复合材料螺旋桨非定常空化流固耦合研究

张 晶，张晨星，王 惠，梁欣欣，吴 钦

（1.北京宇航系统工程研究所，北京 100076；2.北京理工大学机械与车辆学院，北京 100081）

0 引 言

船用螺旋桨大多采用锰-镍-铝-铜/青铜（MAB、NAB）合金制成，虽然屈服强度高，可靠性较好，但存在因阻尼性能差而易产生振动噪声、易空蚀和易疲劳破坏等问题，直接限制其服役寿命及推进性能[1-3]。纤维增强聚合物基复合材料由于具有高比强、耐腐蚀、耐疲劳、阻尼减振性好和性能可设计等优势，已在航空航天等领域得到广泛应用[4-5]。近年来，利用先进复合材料研制性能优异的新型船用螺旋桨备受关注[6]。

与可忽略水弹性响应的刚性金属螺旋桨不同，针对复合材料螺旋桨的研究必须考虑桨叶与流体之间显著的流固耦合效应[7-9]。然而，目前关于复合材料螺旋桨的研究多是基于CFD 对其敞水性能和结构静力学响应进行的计算分析，对复合材料螺旋桨的瞬态双向流固耦合及空化水动力特性的研究非常少[10-13]。国内外学者对流固耦合算法进行了深入研究，建立了两种经典的算法：完全耦合法和分步耦合法。其中完全耦合法也称整体求解法，通过对流场和结构场建立统一的耦合方程，在一个时间步内对流体域和结构域中所有的未知量同时进行求解；分步耦合法则是分别对流场和结构场选择合适的数值算法进行独立求解，再通过流固耦合交界面进行数据传递直至获得收敛解。按照耦合的紧密程度，可分为松耦合算法和紧耦合算法：松耦合算法是指在一个时间步内，按顺序先求解流场，接着通过流固耦合交界面进行水动力信息传递，再进行结构场有限元计算；紧耦合算法的流程与松耦合算法相似，两者的区别在于紧耦合算法在求解完结构场后的时间步内添加子迭代步，对每一子迭代步的计算结果都进行收敛性判断，使得数值结果更为准确。吴钦等[14]基于完全耦合法对NACA 0009 水翼的流固耦合特性进行了数值研究，揭示了流体与结构的惯性作用对水弹性响应的影响规律；Ryzhakov等[15]应用完全耦合法求解柔性结构与流体间的相互耦合，结果表明该算法可以有效减小附加质量效应对结果的影响。然而在工程领域中，大型且复杂的流固耦合系统往往局限于计算资源与时效而难以采用完全耦合法进行求解，因此分步耦合法得到了更为广泛的应用[16-17]，即分别对流场和结构场选择合适的数值算法进行独立求解，再通过流固耦合交界面进行数据的传递直至获得耦合收敛解。Ducoin等[18]利用分步松耦合算法研究了绕弹性水翼流动的水弹性响应和结构稳定性，结果表明在流场作用下弹性水翼发生绕弹性轴顺时针方向的扭转变形导致有效攻角增大，同时结构的变形加速了流场转捩和失速现象的发生；Hu等[19]基于分步紧耦合算法针对弹性水翼分析了流体载荷、水动力特性与结构变形间的相互作用；陈倩等[20]采用分步紧耦合算法研究了NACA 0009 复合材料水翼的结构变形特性和强度特性，发现复合材料水翼的尖端扭转角随铺层角的增大而减小，并提出无量纲扭转角和无量纲位移来表达复合材料的弯扭耦合特性。

近年来，随着海洋工程等领域的迫切需求，越来越多的学者开始关注非定常空化流固耦合的计算与研究。陈倩[21]对NACA 66 水翼建立非定常空化流固耦合数值计算方法，开展了典型空化和不同云状空化非定常流动机制的空化流固耦合研究，揭示了典型空化阶段及不同云状空化非定常流动机制的空化演变规律及结构振动响应；胡世良[22]建立了三维非定常空化流动-结构耦合动力学仿真计算平台，并对弹性水翼的空化绕流特性进行研究，基于分步紧耦合算法分析了流场载荷作用下弹性结构的响应及其对空化流的影响；Zhang[23]开展了基于空化流固耦合的诱导轮流激振动特性数值计算，此外还对大侧斜复合材料螺旋桨的敞水性能及结构响应做了一定的基础研究，并基于该研究结果提出了一种有效的预变形设计方法，提高了复合材料螺旋桨在设计工况的推进效率[24-25]；张宏磊[26]基于CFD耦合FEM 方法，结合MATLAB 的几何重构程序建立了复合材料螺旋桨空泡数值计算方法，完成了空化工况下复合材料螺旋桨的流固耦合计算，研究了不同工况、不同空泡数下复合材料螺旋桨的空泡水动力性能。

本文在传统金属螺旋桨计算分析的基础上，建立复合材料螺旋桨非定常空化流固耦合数值计算方法，分析复合材料螺旋桨在非均匀伴流中的非定常空化水动力性能及桨叶结构动态响应，对比复合材料和刚性螺旋桨的叶梢空泡演化过程及空化特性的不同，揭示因复合材料的应用使螺旋桨推进效率得以提高、叶梢空化得以抑制的机理，对改善螺旋桨空泡性能及提高船舶航行稳定性具有一定参考价值。

1 非定常空化流固耦合数值计算方法

1.1 复合材料螺旋桨结构有限元模型

本文以日本Seiun-Maru 船用大侧斜模型螺旋桨（M-HSP）为研究对象，其几何参数如表1 所示。以碳纤维增强环氧树脂复合材料作为螺旋桨结构有限元模型的工程材料，材料参数如表2所示。纤维铺层方式为[30°5/60°5/60°5/15°5/15°5]s，如图1所示，以从螺旋桨导边指向随边为纤维0°铺层参考方向。由于水动力载荷压力梯度较大且具有非线性特征，故采用三维20 节点SOLID 186 单元对复合材料桨叶进行结构化网格划分，螺旋桨旋转速度为1050 r/min，桨叶根部为固支约束，桨叶表面设置为流固耦合交界面，以实现结构场与流场之间力和位移的数据传递。复合材料螺旋桨旋转时，叶片受到水动力载荷和离心力作用而产生变形，变形后的桨叶将改变螺旋桨周围流场，同时流场载荷的变化又将再次改变桨叶结构的变形。将桨叶结构动力学方程在时域内进行离散：

表1 螺旋桨几何参数Tab.1 Geometric parameters of M-HSP

表2 碳纤维复合材料参数Tab.2 Properties of carbon fiber

图1 复合材料螺旋桨有限元模型Fig.1 Finite element model of the composite material propeller

1.2 复合材料螺旋桨外流场数值模型

外流场计算域分为静止域与旋转域两部分，具体尺寸如图2 所示。在流域入口端设置长0.8D（D为螺旋桨直径）的静止域来充分模拟船尾流场以保证计算准确性[27]。入口来流条件采用实验获得的非均匀尾流速度场分布[28]，出口定义为压力出口，桨叶和桨毂设置为无滑移壁面，静止域和旋转域间采用滑移网格技术Transient Rotor Stator 模型实现动静交界面连接，旋转域的转速与结构场保持一致。为精确捕捉叶片附近压力脉动和桨叶负载，在旋转域内部螺旋桨周围建立半径为0.75D的小圆柱体域，如图3 所示，采用适应性较强的非结构网格并作加密处理，静止域与旋转外域均采用六面体单元进行结构化网格划分。针对空化流动的计算，采用均相流模型进行求解，其中连续性方程和动量方程分别为

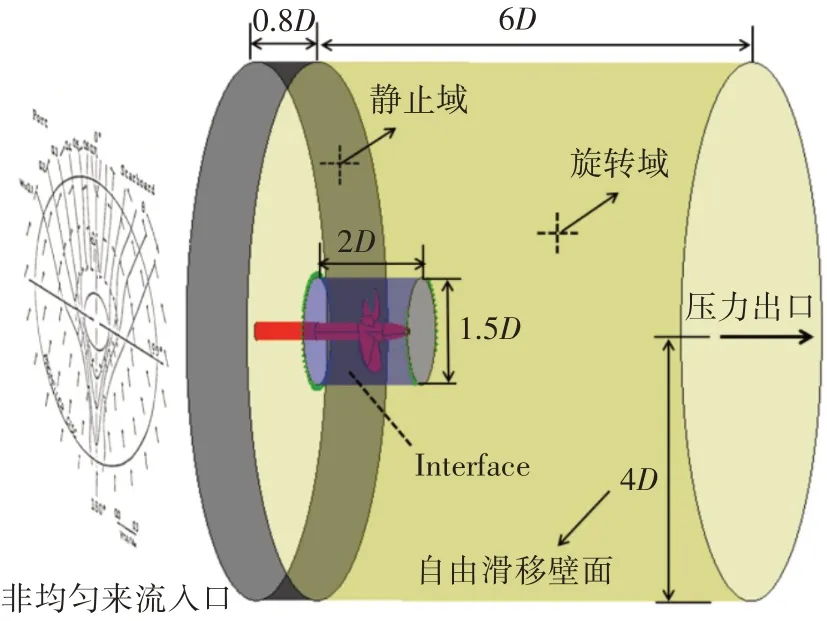
图2 外流域及边界条件Fig.2 Fluid domain and boundary conditions

图3 桨叶附近网格Fig.3 Grids near blades

式中，下标i、j代表坐标方向，u为流场速度，p为流场压力，ρm为混合介质密度，μm为混合介质的动力粘性系数，μt为湍流粘性系数。其中混合项的介质密度ρm和介质动力粘性系数μm的定义分别为

式中，ρl和ρv分别为液相和汽相流体的密度，αl和αv分别为液相和汽相的体积分数，μl和μv分别为液相和汽相流体的运动粘度。此外，计算采用k-ωSST湍流模型和Kubota空化模型，具体方程见文献[29]。

1.3 双向流固耦合数值计算方法

基于ANSYS 平台的System Coupling 模块，采用紧耦合算法来计算复合材料螺旋桨外流场与桨叶结构场之间的数据传递和耦合效应。图4 给出了所用双向流固耦合算法(Bi-FSI)的示意图，其中整个瞬态求解过程由多个时间步（Time Step 1，2，…，i）组成，在每一时间步内，流场和结构场进行交错迭代（Stagger）计算，每一次交错迭代计算中包括多个子迭代步（Iteration Step 1，2，…，j）计算，每一子迭代步中进行一次流场与结构场之间力（Force）和位移（Displacement）的数据传递。在流场或结构场的单独求解过程中，根据单元类型、求解方法、载荷输入等步骤完成各物理场求解（Field Solution）。此外在流固交界面上，流体和结构的应力（τ）、位移（d）和其他变量应相等或守恒，在流体网格和结构网格之间采用Conservative插值算法来传输数据，收敛目标值均设置为0.01。

图4 流固耦合计算方法示意图Fig.4 Schematic diagram of FSI method

2 结果与讨论

2.1 数值方法验证

为了验证螺旋桨非定常空化数值计算方法的准确性，对比了典型空化工况下（J=0.789，σ=2.99）刚性螺旋桨在一个旋转周期内数值计算的推力系数KT-HSP 及扭矩系数10KQ-HSP 和实验测量[30]的KT-Exp 及10KQ-Exp，如图5 所示。由图可以明显地观察到五个正弦峰，与螺旋桨五个桨叶依次进入高伴流区相对应。图中还给出了数值结果时均值与实验值间的误差分别为5.42%和1.56%，故所用数值计算方法可以准确地预测该螺旋桨的空化水动力性能。

图5 一个周期内螺旋桨推力系数及扭矩系数与实验的对比Fig.5 Comparison of thrust coefficients and torque coefficients with experiment in one cycle

空泡形态的模拟精度是验证非定常空化数值计算方法准确性不可或缺的一部分，如图6所示，将仿真得到的桨叶处在不同位置时叶梢空泡的演化过程与实验结果进行了对比，其中以水蒸气体积分数为10%的等值面来表征空泡形态。由图可知，叶梢空泡从导边开始初生，随后沿导边向叶梢生长且空泡体积不断膨胀，逐渐在叶梢形成梢涡空化。数值模拟获得的空泡形态发展过程与实验结果吻合得较好。

图6 实验与数值计算空泡形态的对比Fig.6 Comparison of experimental and numerical bubble shapes

为了验证空化工况下捕捉压力脉动的准确性，对螺旋桨上方的三个监测点（P1、C、S1）进行了压力脉动计算，其中监测点具体坐标详见文献[30]。以监测点C为例，如图7（a）所示，压力脉动分量主要集中在各阶主叶频上(一阶主叶频f=nZ=87.5 Hz)，这是由于压力脉动的最大公共周期为桨叶通过高伴流区的频率。其他两个监测点也采用相同的处理方法，得到图7（b）所示的一阶主叶频压力脉动幅值与实验的对比，三个监测点的一阶主叶频压力脉动幅值大小及其分布趋势与实验基本保持一致。

图7 压力脉动捕捉准确性验证Fig.7 Accuracy verification of pressure fluctuation capture

2.2 复合材料螺旋桨瞬态空泡演化及结构响应

由于高伴流区的存在，如图8 所示，复合材料与刚性金属螺旋桨叶梢空泡的演化分为四个阶段：（a）空泡于导边初生；（b）沿导边向叶梢生长；（c）梢涡空泡形成；（d）急剧收缩后溃灭。图中以红色高亮展示叶梢空泡形态，蓝色为复合材料桨叶的总变形量。为了直观展示螺旋桨叶片的旋转运动，图中还给出了不同阶段流线的分布。如图8（a）所示，随着桨叶进入高伴流区，空化首先在桨叶导边初生并发展起来，细条状空泡附着在导边中上段，桨叶总变形沿导边和随边从叶根到叶梢呈带状阶梯型分布，且变形量逐渐递增，叶梢的总变形最大，桨叶中下大部区域几乎没有变形。随着桨叶的旋转，流线大部分处于吸力面侧，如图8（b）所示，细条状空泡沿导边向叶梢生长，逐渐变厚变长，除带空泡桨叶外其余桨叶最大变形量均减小。直到发展至图8（c）时刻，桨叶旋转到伴流峰附近，条状空泡到达叶梢形成明显的梢涡空泡，同时空泡体积达到最大，叶梢变形量也达到最大。之后随着桨叶逐渐离开高伴流区，如图8（d）所示，梢涡空泡开始沿叶根向叶梢方向急剧收缩，直至在叶尖处溃灭，此时桨叶的最大变形量和其余桨叶大致相同。

图8 复合材料及刚性金属螺旋桨叶梢空泡的演化Fig.8 Evolution of cavitation in composite material propeller and rigid propeller

为了研究桨叶变形与叶梢空化之间的关系，图9 给出了空泡演化的四个阶段里桨叶最大变形量的变化以及有限元计算所得的桨叶变形。由图可知，叶梢最大变形量随叶梢空化的初生、发展而逐渐增大，在梢涡空泡形成阶段达到的最大值为1.69E-4 m，然后随着空泡的溃灭而减小，但仍高于空化初生阶段的最大变形量。这是由于随着空泡的发展，桨叶吸力面与压力面的压差及其作用范围逐渐增大，从而使桨叶受到逐渐递增的水动力载荷，最大变形量随之增大。

图9 四个阶段桨叶最大变形量的变化及桨叶变形云图Fig.9 Variation of maximum deformation of blade in four stages

为了细致地研究复合材料与刚性金属螺旋桨叶梢空泡的演化，图10给出了1号桨叶弦向s=0.5的示意图及r/R=0.9上三个监测点的位置。图11为复合材料及刚性金属螺旋桨叶片弦向s=0.5上在一个旋转周期内的空泡体积分数时空分布图，其中（a）、（b）分别为复合材料螺旋桨的吸力面及压力面，（c）、（d）则分别为刚性金属螺旋桨的吸力面及压力面。两种材料螺旋桨的空泡体积分数分布基本一致，在吸力面上，空泡主要存在于0.75R～0.95R位置，在0.9R达到最大值时，其中复合材料螺旋桨上的最大值为0.43，而刚性金属桨上则为0.562。在压力面上，空泡存在的范围相较于吸力面较小，仅分布在桨叶0.9R以上并在叶梢达到最大值，其中复合材料螺旋桨的空泡体积分数最大值为0.41E-5，而刚性金属桨为2.65E-5，其它区域均为0，基本可认为桨叶压力面上没有空泡。图中红色虚线标注出了空泡在复合材料螺旋桨叶片上存在的时间∆Ta、∆Tb；黄色虚线则代表空泡在刚性金属螺旋桨叶片上存在的时间∆Tc、∆Td。由图可以明显看出∆Tc>∆Ta、∆Td>∆Tb，也即复合材料螺旋桨上的空泡存在时间要小于金属螺旋桨上的，此外，刚性金属螺旋桨的空泡初生时间要早于复合材料桨的，其空泡溃灭时间要晚于复合材料桨，说明复合材料的应用可以延迟空化初生并抑制空化发展。

图10 Blade1上弦向及径向监测点示意图Fig.10 Schematic diagram of chordal and radial monitoring points on Blade1

图11 复合材料/刚性桨叶片弦向s=0.5空泡体积分数时空分布图Fig.11 Space-time distribution of cavitation volume fraction of composite material/rigid blade chord direction s=0.5

图12 为复合材料螺旋桨及刚性金属桨叶片在两个旋转周期上三个监测点的非定常压力脉动演化对比。由图可知，两种材料的螺旋桨压力脉动趋势大致一致，但存在值得研究的显著区别。初始时刻，随着桨叶进入高伴流区，3个监测点的绝对压力骤降，两种材料的螺旋桨在旋转周期内由伴流引起的脉动压力具有最大的幅值，随后，刚性金属桨靠近导边的两个监测点Point 1和Point 2的绝对压力骤降至饱和蒸汽压3169 Pa，并持续一段时间，此时空化开始初生并沿导边生长，而复合材料螺旋桨的空化初生时间晚于刚性金属桨。在t=0.01 s时刻，随着桨叶离开高伴流区域，伴随着空泡的溃灭，两种材料的螺旋桨压力开始快速爬升，刚性金属桨的脉动压力达到最大峰值，此时复合材料螺旋桨的脉动压力较之偏低，如图中第一个紫色箭头所示。随后刚性金属桨的脉动压力开始下降并逐渐平稳，但随着桨叶的旋转，其脉动压力出现多个脉动峰，直至下一个周期的到来。与刚性金属桨相比，复合材料螺旋桨的压力脉动峰值较为缓和，整体负荷较平稳，对非均匀伴流场的适应性更好。

图12 复合材料螺旋桨及刚性金属桨叶非定常压力脉动演化Fig.12 Evolution of unsteady pressure fluctuation of composite material propeller and rigid propeller blade

2.3 复合材料对螺旋桨非定常空化性能的影响

为了研究复合材料的应用对螺旋桨非定常空化性能的影响，对比了复合材料螺旋桨及刚性金属桨上经过伴流峰的桨叶空泡体积的大小，如图13 所示。由图可知，在一个旋转周期内，两种材料的螺旋桨空泡体积经过生长、溃灭的周期过程呈正弦状演化，且由于五个叶片在一个旋转周期内依次经过伴流峰，故其空泡体积也存在五个峰值，空泡体积峰值位置对应的旋转角度与桨叶旋转至伴流峰的时刻相对应，此刻空泡到达叶梢并形成体积最大的梢涡空泡。此外，可以明显看出在一个旋转周期内复合材料螺旋桨的空泡体积均小于刚性金属桨，可见复合材料的应用可有效抑制空化，且复合材料螺旋桨的空泡体积在生长阶段要晚于刚性金属螺旋桨，而在溃灭阶段要早于刚性金属螺旋桨，可见复合材料的应用可延迟叶梢空化的初生。

图13 复合材料螺旋桨及金属桨叶空泡体积的对比Fig.13 Comparison of cavitation volumes of composite material propeller and metal blade

为了解释复合材料螺旋桨吸力面压力相较于刚性金属桨有所上升的原因，图15给出了桨叶螺距角及攻角的示意图，在相同工况下（J=0.789），刚性桨与复合材料桨的来流角相等，均为θJ=0.789，在水动力载荷作用下，刚性桨的螺距角保持不变，而复合材料螺旋桨叶片因弯扭耦合效应在吸力面压力过低时发生扭曲，使得其螺距角发生减小。由于复合材料螺旋桨的攻角αcomposite=ϕcomposite-θJ=0.789，故其攻角也随之减小。因此，攻角的减小使得复合材料螺旋桨叶片吸力侧的压力得以提升，进而抑制了叶梢空化的发展。

图15 桨叶螺距角及攻角示意图Fig.15 Schematic diagram of blade pitch angle and attack angle

为了研究复合材料的应用对螺旋桨空化水动力性能的影响，对比了典型空化工况（J=0.789，σ=2.99）下一个旋转周期内复合材料螺旋桨和刚性金属螺旋桨的推力系数及扭矩系数，如图16所示。KT和10KQ随时间演化的五个正弦峰正好与螺旋桨五个桨叶依次进入高伴流区相对应。与无耦合的刚性桨相比，在流固耦合作用下复合材料桨的推力系数KT稍有降低，而10KQ有明显降低，这是由于在非定常水动力载荷作用下复合材料桨叶发生了弯曲和扭转变形，导致桨叶各半径叶切面处的螺距角减小。此外，图17还给出了两种材料的螺旋桨推进效率的对比，由图可知，复合材料的应用使得螺旋桨推进效率稍有提升，这是由于复合材料螺旋桨所需扭矩相对较小的缘故。

图16 复材桨及金属桨的推力系数及扭矩系数Fig.16 Thrust coefficient and torque coefficient of composite material propeller and rigid propeller

3 结 论

本文基于建立的复合材料螺旋桨非定常空化流固耦合数值计算方法，系统研究了典型空化数下复合材料与刚性金属螺旋桨的叶梢空泡演化及结构响应，分析了复合材料对螺旋桨非定常空化性能的影响。主要研究结论如下：

（1）对比了复合材料与刚性金属螺旋桨的叶梢空泡演化。由于高伴流区的存在，叶梢空泡演化分为四个阶段：（a）空泡于导边初生；（b）沿导边向叶梢生长；（c）梢涡空泡形成；（d）急剧收缩后溃灭。叶梢最大变形量随着叶梢空化的初生、发展而逐渐增大，在梢涡空泡形成阶段达到最大值，然后随着空泡的溃灭而减小。

（2）揭示了典型空化数下非均匀来流中因复合材料的应用使螺旋桨空化得以抑制的机制。刚性金属螺旋桨的空泡初生时间早于复合材料桨，其空泡溃灭时间晚于复合材料螺旋桨。攻角的减小使得复合材料螺旋桨叶片吸力侧的压力得以提升，进而抑制了叶梢空化的发展。

（3）复合材料的应用可以提高螺旋桨推进效率，这是由于复合材料螺旋桨所需扭矩相对较小的缘故。与刚性金属桨相比，复合材料螺旋桨的压力脉动峰值较为缓和，整体负荷较平稳，对非均匀伴流场的适应性更好。