多种动力学模型应用于废旧轮胎的热解机理研究
单体仑,高晓东,田晓龙*,边慧光,王孔烁,李朝阳,汪传生
(1.青岛科技大学 机电工程学院,山东 青岛 266061;2.中国核电工程有限公司,北京 100840)
汽车现已成为家庭必备的交通工具,为出行带来便利的同时,随之产生了大量的废旧轮胎[1]。据估计,全球每年约产生10亿条废旧轮胎,并且伴随汽车的不断发展,废旧轮胎的数量仍在不断增加[2-3]。目前世界轮胎存在产量大、回收率低、在自然界降解周期长等问题,若废旧轮胎无法妥善处理而随意丢弃,轮胎中的化学添加剂会逐渐渗入到土壤或水源中,极易对人体和环境造成严重危害[4-6]。热解是一种清洁且具有广阔前景的化学回收技术,将其应用于废旧轮胎回收可生产能源和具有高附加值的化学产品[7-8]。
近年,国内外学者对废旧轮胎的热解进行了大量研究,包括对热解技术、热解产物及热解机理的研究。W.LUO等[9]研究低成本粘土(包括不同粒径的高岭土和用ZnCl2和HCl改性的蒙脱土)作为催化剂对废旧轮胎热解产物的影响,结果表明粘土可以提高热解产物的质量和回收率,粘土的粒径和改性条件对热解产物的分布和组分存在显著影响。D.CZAJCZYÑSKA等[10]在不同温度(400,500和600 ℃)下对废旧轮胎进行热解,并对获得的热解产物进行研究,其中热解气的高热值随温度的升高而减小,温度为400 ℃时热解油的产率最高。S.FRIGO等[11]在中等温度(300~500℃)下热解废旧轮胎以制备液体燃料,通过标准方法分析得出热解油的燃料性质(密度、粘度、热值和闪点)与商业柴油燃料相当。N.M.MKHIZE等[12]使用克级热解反应器(固定床)和微克级热解反应器[热重(TG)分析仪]研究热解温度和升温速率对废旧轮胎热解过程中柠檬烯产量的影响,结果表明热解温度对轮胎衍生油的影响显著,而升温速率和热解温度的共同作用对柠檬烯的产率存在影响。J.HAYDARY等[13]研究轮胎胶粉粒径和热分解动力学对热解时间的影响,结果表明胶粉粒径与完全热解时间呈正比,并且轮胎热解分为2个阶段,第1阶段的活化能(E)和指前因子(A)分别为79.9 kJ·mol-1和3.87×103s-1,第2阶段E和A分别为128.4 kJ·mol-1和1.57×107s-1。
研究[14]表明,无模型法是一种快速获取动力学信息的计算方式,但此类模型一般只能获得基本的E,而无法确定最概然机理函数。与无模型法不同,模型拟合法能够同时获得不同反应机理模型下的动力学参数(E和A)。通过无模型法和模型拟合法相结合的方式可快速计算废旧轮胎的动力学参数,并确定最概然热解机理函数模型。
目前,针对热化学法处理废旧轮胎的研究较多,但同时采用多种动力学模型评估动力学参数的研究较少。
本工作通过TG分析法研究不同升温速率下废旧轮胎的热解机理,并通过无模型法[Flynn-Wall-Ozawa(FWO)法、Kissinger-Akahira-Sunose(KAS)法、Starink法、Friedman法和Kissinger法]和模型拟合法[Coats-Redfern(C-R)法]计算动力学参数,判断动力学模型之间计算结果的差异以及研究废旧轮胎的热解机理,为废旧轮胎热解反应器设计和工业化提供理论基础。
1 实验
1.1 主要原材料
采用的废旧轮胎来自青岛一家废品回收站。测试前先将废旧轮胎粉碎,然后经过磁选去除所含的钢丝和铁屑,剩下材料在80 ℃×2 h条件下烘干即完成样品制备。试验和计算流程如图1所示。
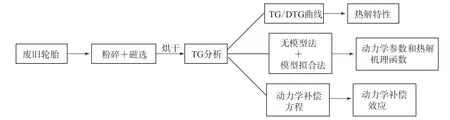
图1 试验和计算流程Fig.1 Experiment and calculation processes
1.2 TG分析
TG分析是一种基本的热分析方法,它可精确地检测可控气氛流量、加热速率、温度和样品质量的变化[15]。本试验TG分析采用德国耐驰仪器制造有限公司的NETZSCH TG 209 F3 Tarsus型TG仪,设置10,20,30,40 ℃·min-1四种升温速率。每次试验将约10 mg样品放入氧化铝坩埚中,在氮气气氛(吹扫气和保护气的流量速率分别为50和20 mL·min-1)下从40 ℃加热至800 ℃。
1.3 动力学模型表达式
固体热解的广泛表达式为:
式中,k(T)为反应速率常数,f(α)为反应机理函数,T,t和α分别为绝对温度(K)、反应时间(min)和反应转化率(%),m0,mt和m∞分别为样品在初始、瞬时和最终的质量(mg)。
式(1)中k(T)的表达式为:
式中,R为理想气体常数(8.314 J·mol-1·K-1)。
升温速率(β)表达式为:
通过式(1)—(4)得废旧轮胎热解过程中的非等温、非均相热解的表达式为:
本研究采用无模型法和模型拟合法进行动力学参数计算,判断动力学模型对计算结果的影响,并确定最概然机理函数。
1.3.1 无模型法
在不假设反应机理的前提下,无模型法可获得较为精确的E计算结果,在动力学研究中被广泛应用。本研究中采用的无模型法包括FWO法、KAS法、Starink法、Friedman法和Kissinger法。
FWO法的动力学模型表达形式为:
KAS法的动力学模型表达形式为:
Starink法的动力学模型表达形式为:
Friedman法的动力学模型表达形式为:
Kissinger法的动力学模型表达形式为:
式中,G(α)为反应机理函数的积分形式,Tp为最大质量损失温度。
式(6)—(9)计算过程中以1/T为横坐标和分别以lnβ,ln(β/T2),ln(β/T1.8),ln(βdα/dt)为纵坐标进行拟合;式(10)以1/Tp为横坐标和以ln(β/Tp2)
为纵坐标进行拟合,通过拟合曲线的斜率和截距计算得到E和A。
1.3.2 模型拟合法
模型拟合法可快速确定样品热解过程中最概然机理函数,并将确定的机理函数代入无模型法计算出对应模型的A。本试验中采用的模型拟合法为C-R法。
C-R法的动力学模型表达式为:
式(11)计算过程中以1/T为横坐标和以ln[G(α)/T2]为纵坐标进行曲线拟合,通过拟合曲线的斜率和截距计算得到E和A,根据E和相关因数(r2)判断最概然机理函数。常见C-R法的热解机理函数表达式如表1所示。

表1 常见C-R法的热解机理函数表达式Tab.1 Expressions of common pyrolysis mechanism functions of C-R method
1.3.3 动力学补偿效应
动力学补偿效应可用于检验所选反应模型的正确性[16]。一般来说,如果选定的反应机理函数G(α)适合于表征固体热解,那么lnA与E之间存在线性关系[17],如式(12)所示。
式中,a和b为补偿参数。
式(12)计算过程中,以不同转化率的E为横坐标和lnA为纵坐标进行曲线拟合,拟合曲线的斜率和截距分别为a和b。
2 结果与讨论
2.1 热解特性分析
在惰性氮气气氛下,废旧轮胎的TG/热重微分(DTG)曲线如图2所示。

图2 废旧轮胎的TG/DTG曲线Fig.2 TG/DTG curves of waste tire
从图2可以看出,废旧轮胎的热解温度主要集中于230~500 ℃之间,热解过程中只存在1个明显的质量损失峰,表明热解过程一步完成。G.Y.CHEN等[18]认为分子侧基断链和主链断裂是橡胶解聚的主要原因,其中主链断裂主要发生在天然橡胶(NR)、丁苯橡胶(SBR)和聚丁二烯橡胶(BR)中。T.MENARES等[19]研究认为废旧轮胎的热解过程分为8个步骤:前2个分解步骤发生在100~200 ℃,与增塑剂的降解有关,对应的质量损失可以忽略不计;第3和4个分解步骤发生于230~300 ℃,这归因于NR和BR形成自由基;在330~420 ℃,第5—7分解步骤发生的主要反应是NR和SBR的解聚,形成单/二聚体以及脱挥发分/缩合反应,此时质量损失最大;最后,DTG曲线在430 ℃左右处有1个宽峰值,这主要与分子主链的碳-碳单键断裂和发生缩合反应形成碳-碳双键有关,整个热解过程约在510 ℃完成。随着升温速率的增大,废旧轮胎的热解温度发生滞后现象,与之对应的降解速率逐渐增大,但达到相同转化率所需的温度更高。
不同升温速率下废旧轮胎的热解特性参数如表2所示。

表2 不同升温速率下废旧轮胎的热解特性参数Tab.2 Pyrolysis characteristic parameters of waste tire under different heating rates
从表2可以看出,随着升温速率的增大,热解温度区间逐渐增大,最终残余质量保持一致,说明升温速率影响废旧轮胎的热解温度区间,但对残余质量不产生影响。
2.2 动力学参数分析
基于一级反应模型对废旧轮胎进行动力学分析,通过FWO法、KAS法、Starink法、Friedman法和Kissinger法得出的动力学参数如表3所示。

表3 不同无模型法下废旧轮胎的动力学参数Tab.3 Dynamic parameters of waste tire under different model-free methods
从表3可以看出,Kissinger法只能获得单一的动力学参数,而FWO法、KAS法、Starink法和Friedman法的动力学参数是范围值,故Kissinger法的计算精确度最小。E和A的计算结果由大到小的动力学模型依次为Friedman法、FWO法、Starink法、KAS法、Kissinger法。不同动力学模型下废旧轮胎的动力学参数的相关因子(r2)均大于0.97,表明拟合结果可靠[20-21]。
废旧轮胎热解过程中E和A会随α的改变而改变,所以采用等转化率法研究废旧轮胎的热解过程更为准确。不同α对应的E和A如图3所示。

图3 不同α对应的E和AFig.3 E and A corresponding to different α
从图3可以看出:FWO法、KAS法和Starink法计算的E变化趋势相同,且均小于Friedman法;FWO法计算的A明显大于KAS法和Starink法,这可能与动力学模型的选择有关。
不同文献的废旧轮胎的E计算结果如表4所示,试验均在氮气气氛下进行。

表4 不同文献的废旧轮胎的E计算结果Tab.4 Calculation results of E of waste tire from different literatures
从表4可以看出,不同文献的E存在差异,这可能与材料来源和试验条件等有关。
2.3 最概然机理函数拟合分析
基于C-R法拟合废旧轮胎热解过程中不同机理函数模型对应的E如表5所示。

表5 基于C-R法的不同升温速率下E的计算结果Tab.5 Calculation results of E at different heating rates based on C-R method
从表5可以看出:升温速率对E的拟合结果存在影响,即随着升温速率的增大,E增大,r2无明显变化规律;D3模型的r2最大,E最接近无模型法计算结果,故将废旧轮胎热解过程中遵循的机理函数模型确定为D3。
2.4 动力学补偿效应分析
将不同α下E和A代入式(12)可得不同动力学模型下的动力学补偿效应公式,计算结果如表6所示。

表6 不同动力学模型对应的补偿方程Tab.6 Compensation equations corresponding to different kinetic models
从表6可以看出,4种动力学模型的r2大于0.99,说明lnA和E之间存在良好的线性关系,机理函数模型选择合适。动力学补偿效应的可靠度大小依次为KAS法、Friedman法、Starink法、FWO法。
3 结论
(1)Kissinger法仅获得单一的动力学参数,而FWO法、KAS法、Starink法和Friedman法的动力学参数是范围值,Kissinger法的计算精确度最小。
(2)采用等转化率法计算动力学参数时,FWO法、KAS法和Starink法计算的E变化趋势相同,且均小于Friedman法;FWO法计算的A明显大于KAS法和Starink法。
(3)采用C-R法确定最概然机理函数时,随着升温速率的增大,E增大,r2无明显变化规律;废旧轮胎热解过程中遵循的机理函数模型为D3。
废旧轮胎TG分析和动力学模型建立的整合有利于对其热解机理深入了解,可为废旧轮胎的热解处理提供理论支持。

