不同地震激励方向下隔震曲线梁桥易损性分析
李喜梅 蒲奎 杨国俊 母渤海


摘要:为进一步评估隔震曲线梁桥在地震激励下的抗震性能,从地震易损性角度出发并兼顾考虑地震激励方向对其易损性的影响。利用APDL建立采用板式橡胶支座的隔震曲线梁桥有限元模型,从PEER中选取同一地震事件中的近断层地震动,按规范规定比例输入水平双向地震动进行非线性动力时程分析,结合地震响应与损伤指标计算得到各构件地震易损性曲线;考虑地震激励方向的变化,通过MATLAB编程绘制得到桥梁结构构件(桥墩与支座)以及整体系统的地震易损性曲面,分析探讨地震激励方向对隔震曲线梁桥易损性的影响。结果表明:不同极限状态下各桥墩切向损伤条件概率明显大于其径向,各支座的切向与径向易损性相差不大,但仍是各支座的切向易损性略大于径向易损性;桥梁各构件(桥墩与支座)切向易损性对地震激勵方向均表现出很强依赖性,而径向易损性对其的依赖性相对较弱,且伴随损伤等级的提高,构件易损性对地震激励方向更加敏感;桥梁整体系统易损性对地震激励方向的变化不太敏感,且因各构件响应之间的相关性较高,其系统易损性更接近于易损性最大的构件——易损性下限;当进行隔震曲线梁桥抗震性能评估时,应考虑不同地震激励方向对其地震易损性的影响,从而使得易损性分析结果更加合理,能够更加真实地反映隔震曲线梁桥的实际损伤状态。
关键词:隔震曲线梁桥; 抗震性能; 地震激励方向; 易损性曲面
中图分类号: TU352.1 文献标志码:A 文章编号: 1000-0844(2024)01-0026-13
DOI:10.20000/j.1000-0844.20211230002
Fragility analysis of isolated curved girder bridges under different seismic excitation directions
Abstract:
To further evaluate the seismic performance of isolated curved girder bridges under seismic excitation, the influence of seismic excitation direction on their fragility was studied. A finite element model of an isolated curved girder bridge with laminated rubber bearings was established by APDL. Near-fault ground motions in the same seismic event were selected from PEER, and horizontal bidirectional ground motions were input according to the proportion specified in the code for nonlinear dynamic time-history analysis. The seismic fragility curves of the components were calculated by combining the seismic response and damage index. Considering the change in seismic excitation direction, seismic fragility surfaces of the components (pier and bearing) and bridge system were obtained using MATLAB programming and the influence of seismic excitation direction on the fragility of the isolated curved girder bridge was analyzed and discussed. The results show that under different limit states, the tangential damage probability of each pier is obviously greater than that in the radial direction. The tangential fragility of each bearing is slightly greater than the radial fragility, with little difference. The tangential fragility of bridge members (pier and bearing) strongly depends on the seismic excitation direction, whereas the dependence of radial fragility is weaker; with an increasing damage level, the fragility of members becomes more sensitive to the seismic excitation direction. The fragility of the bridge system, which is insensitive to changes in the seismic excitation direction, is closer to that of the most vulnerable component because of the high correlation between the responses of the components. When evaluating the seismic performance of the isolated curved girder bridges, the influence of the seismic excitation direction on their seismic fragility should be considered to make the fragility analysis results more reasonable and reflect their actual damage state more accurately.
Keywords:
isolated curved girder bridge; seismic performance; seismic excitation direction; fragility surface
0 引言
因对地形、地物等因素限制而特有的空间适应性以及优美的线型,曲线梁桥在公路及城市道路中广泛应用。地震激励下,曲线梁桥因平面不规则性导致结构地震响应相较于直线梁桥更加复杂。自1971年San Fernando地震发生以来,历次强震作用下均出现较为严重的曲线梁桥震害[1-3],对于曲线梁桥的抗震问题研究已取得了一定成果。
为研究地震激励下曲线梁桥的地震响应规律,Jeon等[4]、游新等[5]分析了曲率、墩高等因素对曲线梁桥地震响应的影响,通过对比分析得到显著影响地震需求的结构几何参数;文献[6]从地震动特性出发,分析了不同类型地震激励下曲线梁桥的动力响应,研究发现近断层速度脉冲地震激励下响应更加显著;陈彦江等[7]、Li等[8]进行了曲线梁桥的振动台试验,研究了地震激励下的纵坡、墩高等因素对其地震响应影响。此外,李喜梅等[9]借助MATLAB软件建立了隔震曲线梁桥的简化分析模型,提出多维地震激励下曲线梁桥的最不利激励方向确定方法,为后续最不利激励方向的研究提供参考;基于构件合力方法,冯睿为等[10]推导出曲线梁桥最不利激励方向的计算公式,该方法可靠性较高且能够反映构件整体的受力性能随激励方向的变化规律;梁瑞军等[11]则从地震动随机性的角度出发,研究了地震激励方向与强度随机性对隔震曲线梁桥动力响应的影响,表明激励方向对曲线梁桥地震响应有显著影响。因此,对于地震激励方向的研究成为曲线梁桥抗震设计中亟待解决的问题。
目前,以控制地震风险(Risk)与损失(Loss)为目标的新一代基于性能地震工程(Performance-Based Earthquake Engineering,PBEE)正成为国际地震工程领域的研究热点。其中,对于地震激励下桥梁结构易损性的研究也逐渐得到学者们的关注[12-13]。李宏男等[12]与文献[13]分别综述了国内与国外桥梁易损性研究现状,并对易损性分析方法及相关理论进行了详细总结归纳。Taskari 等[14]与Xu等[15]从构件角度出发研究了不同地震激励方向下曲线梁桥的桥墩易损性变化规律,结果表明低墩所受损伤程度较小。通过考虑地震动与材料特性等因素的不确定性,Abbasi等[16]研究了不同极限状态下曲率半径与墩高比对曲线梁桥易损性曲线的影响,并根据易损性敏感度划分了主要构件与次要构件。分别从构件及系统易损性层面出发,Shirazi等[17]研究发现土壤条件及地震动特性对曲线梁桥地震易损性有一定影响,并指出地震激励方向对易损性的影响同样不可忽略。
以往对于曲线梁桥抗震性能的研究,主要从地震目標响应(墩顶位移、支座位移等)角度入手分析其所受地震激励方向的影响,少有考虑地震激励方向对隔震曲线梁桥易损性的影响。鉴于此,本研究以采用板式橡胶支座的三跨隔震曲线梁桥为对象,利用APDL(ANSYS Parameter Design Language)建立该桥的有限元分析模型,在PEER地震动数据库中选取同一地震事件中的近断层地震动并进行调幅处理,依据一定水平向比例系数[18-19]输入双向地震激励进行地震响应分析,结合损伤指标计算得到其易损性曲线;另外考虑地震激励方向的影响,通过MATLAB编程绘制得到桥梁结构不同构件——桥墩与支座,以及整体桥梁系统易损性曲面;通过研究不同地震激励方向对其地震易损性的影响,可为隔震曲线梁桥的抗震性能评估及抗震设计等提供一定的参考借鉴。
1 工程背景及有限元分析模型
1.1 工程背景
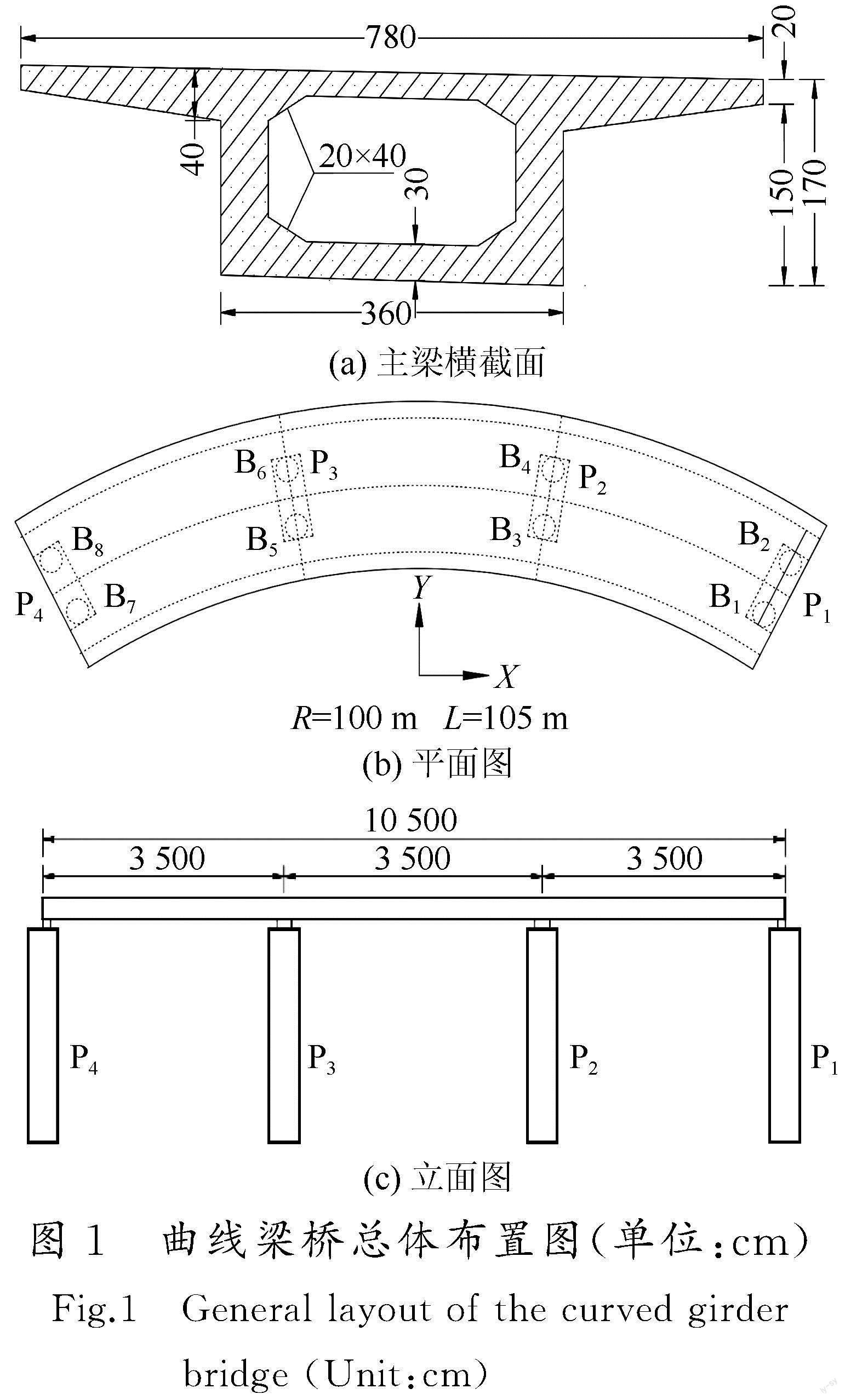
以某曲线梁桥为研究对象进行有限元模型的建立,其桥梁长度为105 m(3×35 m),曲率半径R为100 m,其桥梁总体布置图如图1所示。主梁为现浇混凝土连续箱梁,其横截面采用单箱单室截面,其混凝土强度等级为C50;桥墩为矩形单柱墩,编号为P1~P4,边墩(P1,P4)与中墩(P2,P3)截面尺寸均为3.1 m(长)×1.3 m(宽),墩高均为10 m,混凝土强度等级为C30;支座编号为B1~B8,内外侧支座的偏心距不同,分别为0.85 m、1.15 m。
1.2 有限元模型的建立
(1) 上部结构
地震激励作用下,桥梁上部结构(即主梁)通常情况下无损伤或损失程度较小,可认为其保持弹性状态,故采用弹性梁单元BEAM189模拟。
(2) 隔震支座
由于该隔震曲线梁桥采用了传统的板式橡胶支座,依据结构的对称性及竖向承载力大小选择合适的支座规格,边墩和中墩板式橡胶支座规格分别为GYZ d350×96、GYZ d500×130,其性能参数如表1所列。
每个隔震支座均由水平向(切向和径向)理想弹塑性弹簧单元及竖向弹性弹簧单元组成,分别从ANSYS单元库中选取COMBIN40与COMBIN14单元模拟,其支座本构关系如图2所示。
(3) 下部结构
下部结构(本研究为矩形单柱式桥墩)作为桥梁结构中较为脆弱的构件之一,其在地震作用下进入了塑性变形阶段,在此选用BEAM189的非线性广义梁截面,其是一种抽象的梁截面类型(所谓宏观单元),可直接定义轴力与轴向应变、弯矩与曲率以及扭矩与扭转率等函数关系,从而确定梁单元的刚度方程。非线性广义梁截面所定义的广义力和广义应变的关系如式(1)所列:
式中:N为轴力;M1、M2分别为XZ与XY平面内的弯矩;τ为扭矩;S1\,S2为XZ与XY平面内的剪力;ε为轴向应变;κ1、κ2为XZ与XY平面内的曲率;χ为横截面扭转率;γ1、γ2为XZ与XY平面内的横向剪应变;AE(ε,T)\,IE1(κ1,T)\,IE2(κ2,T)\,JG(χ,T)\,AG1(γ1,T)\,AG2(γ2,T)分别为轴向刚度、XZ和XY平面内的弯曲刚度、扭转刚度,以及XZ和XY平面内的剪切刚度。
(4) Rayleigh阻尼
Rayleigh阻尼是最常用的黏性阻尼模型,也称为比例阻尼(Proportional Damping),即
CRayleigh=αM+βK (2)
式中:α为质量矩阵系数,又称为α阻尼,用ALPHAD定义;β为刚度矩阵系数,又称为β阻尼,用BETAD定义;C、M、K分别为结构的阻尼矩阵、质量矩阵及刚度矩阵。
设结构的第i阶与第j阶固有频率分别为ωi\,ωj,相应的第i阶和第j阶模态阻尼比分别为ξi、ξj,通常假定各阶模态阻尼比相同,即ξi=ξj=ξ,则可求得α和β:
(5) 其他处理
支座与上部结构主梁、下部结构桥墩均采用刚性梁单元MPC184连接,桥墩墩底采用固结形式,未考虑主梁与挡块之间的碰撞以及桩-土相互作用。值得注意的是,ANSYS默认模型建立及分析计算均在直角坐标系下进行,由于曲线梁桥结构的特殊性,其曲率的存在需要建立由柱坐标控制下的局部坐标系(编号必须≥11且为整数),其编号为11~14;此外,不同局部坐标系下建立的桥墩与支座节点及单元均应分别通过节点旋转与单元旋转命令统一在其坐标系下,从而防止计算结果的奇异性而收敛困难甚至无解。所建立的隔震曲线梁桥的有限元简化模型与实体模型分别如图3(a)、图3(b)所示。
1.3 动力特性分析
由表2可知,采用板式橡胶支座的曲线梁桥基频为0.508 Hz,且前4阶阵型主要是主梁的水平向移动,其主要原因是与桥墩相比,支座的水平向剪切刚度较小,其与桥墩形成的串联体系较柔,产生对曲线梁桥的水平约束较小,故自振频率相对较小。该桥的主梁第1阶正对称竖向弯曲振型出现较晚,与文献[20]中支座对于曲线梁桥动力特性影响的一般规律相符。
2 易损性理论与地震动选取及输入
2.1 地震易损性分析理论
概率地震易损性分析作为一种评估单个构件或结构整体,甚至某区域桥梁网络抗震能力的常用方法,其物理意义为在给定强度地震激励下,结构构件或整体系统地震响应需求达到或超越某极限状态抗震能力的损伤条件概率,其研究内容主要包括概率地震需求分析(Probabilistic Seismic Demand Analysis,PSDA)与概率抗震能力分析(Probabilistic Seismic Capacity Analysis,PSCA)。对于前者的研究主要为得到结构工程需求参数(EDP)与地震动强度指标(IM)之间的关系,表示为:
EDP=a(IM)b (5)
式中:a与b均为统计回归系数。
假定上述的地震需求模型服从两参数对数正态分布,则对应的损伤条件概率为:
式中:DI为结构的损伤指数(Damage Index);LS为结构的极限状态(Limit State);βEDP|IM为地震需求与强度指标之间对数线性回归分析所得的标准差。
式中:n为构件的个数。
同时,假设结构构件的抗震能力也服从对数正态分布,并考虑地震激励方向的影响,则其构件易损性函数可表示为:
2.2 损伤指标的确定
作为桥梁结构易损性分析过程中的关键步骤之一,选取合适的损伤指标来量化其所遭受的地震损伤具有非常重要的意义,合理的损伤指标可以更加真实地描述桥梁结构的不同损伤状态,并对易损性分析结果产生显著影响。
(1) 支座损伤指标
文中对于支座损伤状态的判定参考文献[12]中的剪切应变指标,由于隔震支座采用了板式橡胶支座,故得到不同损伤极限状态下的板式橡胶支座的剪切应变界限值,如表3所列。
(2) 桥墩损伤指标
通常情况下,国内外学者采用曲率延性、位移延性以及Park-Ang损伤指标等作为桥墩的性能指标[12-13]。由于该桥梁桥墩为矩形截面,根据矩形桥墩在地震激励下的震害与损伤机理,将其划分为无损伤、轻微破坏、中等破坏、严重破坏与完全破坏五个损伤极限状态,对应四个不同的损伤界限值。由于矩形桥墩在两个不同主轴方向的较大刚度差异,利用软件XTRACT对各桥墩的不同方向(径向与切向)进行弯矩-曲率分析,以墩顶位移延性比为损伤指标,通过式(9)~式(13)计算得到各极限状态损伤界限值,如表4所列。
桥墩首次屈服时的曲率所对应的位移为:
Δdy1=Φ′yL2/3 (9)
同理可得,桥墩等效屈服时对应的位移为:
Δdy=ΦyL2/3 (10)
混凝土应变为0.004对应的位移为:
Δd4=Δdy+Δp
θp=Lp×Φp=Lp×(Φc4-Φy)
Δp=θp×(H-Lp/2) (11)
其中,单柱墩的塑性铰长度为:
Lp1=0.08H+0.022d·fy≥0.044d·fy
Lp2=2b/3
Lp=min(Lp1,Lp2)(12)
故可以得到各损伤界限值分别为:
μdy1=1
μdy=Δdy/Δdy1
μd4=Δd4/Δdy1
μdmax=Δd4+3 (13)
2.3 地震动选取及输入
曲線梁桥在近断层地震激励下的地震响应更剧烈,因此选取同一地震事件(Loma Prieta earthquake)中的10条近断层地震动,其选取记录如表5所列。采用IDA法将所选地震动峰值加速度(PGA)从0.1g调幅至1.0g,加速度增量为0.1g,单一角度进行100次非线性动力时程分析。
我国于2020年最新颁布的《公路桥梁抗震设计规范》对地震激励方向做出规定:当进行曲线桥梁的地震反应分析时,宜分别沿两边墩(或桥台)弦线方向与垂直于弦线方向分别输入纵向与横向地震动,从而进行动力时程分析得到地震激励下的动力响应。采用非线性时程法(Nonlinear Time History Analyses,NTHAs)进行理论易损性计算总量可通过结构对称性而在一定程度上减小[19]。由于该曲线连续梁桥关于横轴[如图2(a)中的Y轴]对称,其计算角度范围减小为-90°≤θ≤90°,又因文中所定义的角度范围均为正值,故其计算范围可转换为0°≤θ≤180°,以30°的角度增量共设7个不同激励方向。
3 隔震曲线梁桥地震易损性分析
3.1 单一激励方向桥墩与支座易损性分析
为研究地震激励下各构件不同方向(切向与径向)的易损性变化规律,以地震激励方向θ为0°时的板式橡胶支座曲线连续梁桥为例,图4与图5分别给出了四种不同极限状态下各桥墩与各内侧支座易损性曲线。
根据各极限状态下桥墩与支座的切向与径向地震易损性曲线,可以得到:
(1) 不同极限状态下各桥墩切向损伤条件概率均明显大于其径向,主要因为矩形桥墩沿两个方向的抗侧移刚度差异所致;不同桥墩的切向易损性曲线在轻微破坏、中等破坏极限状态下相接近,并随着损伤等级的提高易损性曲线之间的差异性增大;其中,4#桥墩切向与径向易损性曲线较其他桥墩差异性更为明显,应关注边墩桥墩的地震响应。
(2) 支座与桥墩不同方向易损性差异性较大,其径向与切向易损性相差不大,但总体来看,仍是各支座的切向易损性大于径向易损性,主要原因是桥梁自身结构响应主要为切向且未考虑桥梁径向挡块对支座变形的限制作用;尤其是,各支座切向与径向易损性变化趋势几乎相一致,不存在类似桥墩易损性曲线急剧增大的情况,主要因为所选取的不同极限状态下支座损伤指标界限值为线性变化关系;此外,边墩支座(1#、7#)相较于中墩支座(3#、5#)更容易发生损伤,主要因为边墩支座的规格相对于中墩支座而言较小,其抵抗变形的能力较差,故抗震设计时应考虑适当增大边墩支座规格。
3.2 不同激励方向下桥墩与支座易损性分析
基于所建立的概率地震需求模型(PSDM)与所定义的能力极限状态,考虑不同地震激励方向对构件易损性的影响,得到在不同损伤极限状态下的构件损伤概率随地震激励方向变化的规律,从而得到其易损性曲面。由于不同极限状态下各桥墩易损性相差不大,以该板式橡胶支座曲线梁桥中1#桥墩为例,利用MATLAB编程实现三维极坐标图像绘制,径向坐标代表峰值加速度PGA,其取值范围为0~1.0g;环向坐标代表地震激励方向,逆时针旋转且取值范围为0°~360°;X轴与Y轴分别代表直角坐标系下的图像投影范围,其切向与径向的易损性曲面在不同极限状态下的损伤概率变化趋势如图6与图7所示。
为进一步阐述桥墩易损性随地震激励方向的变化规律,图8描绘了在轻微破坏极限状态(LS1)下,各桥墩在同一地震动强度(PGA=0.4g)地震激励下对应不同激励方向的切向损伤概率,其余损伤极限状态下的规律与此相似,可类推。
由以上各极限状态下桥墩不同方向易损性曲面与轻微破坏极限状态下各桥墩切向损伤概率雷达图可以看出:
(1) 总体来看,桥墩切向易损性对地震激励方向表现出很强依赖性,即在不同损伤极限状态下其易损性随地震激励方向的变化而产生较大差异,但桥墩径向易损性对激励方向的依赖性相对较弱,表明地震激励方向对桥墩易损性有重要影响;同时,随着损伤等级的提高,各桥墩切向易损性对地震激励方向的变化更加敏感,而径向易损性对激励方向的敏感性相对较弱。
(2) 各桥墩切向易损性总存在特定地震激励方向使其损伤概率达到最大,即“最不利激励方向”,1#与2#桥墩所对应的角度为150°,而3#与4#桥墩所对应的角度为120°;尽管各桥墩可通过易损性分析得到其最不利激励方向,但由于矩形桥墩曲线梁桥其结构的特殊性,与最不利激励方向相邻的角度也应该被考虑,因此建议用“最不利区间角”表达,则该桥梁各桥墩切向最不利区间角为120°~150°。
同样地,因边墩支座损伤可能性相对较大,故用前述方法绘制出边墩位置处1#支座的切向与径向易损性曲面在不同极限状态下的损伤概率变化曲面,如图9与图10所示。可以得到:
支座与桥墩易损性曲面的规律相似,即支座切向易损性对地震激励方向表现出很强依赖性,但其径向易损性对激励方向的依赖性相对较弱,表明地震激励方向同样对支座易损性具有重要影响;随着损伤等级的提高,各支座切向易损性对地震激励方向的变化更加敏感,而径向易损性对激励方向的敏感性相对较弱。由前述对于桥墩“最不利区间角”的建议及说明,可以得到该曲线梁桥各支座切向对应的最不利区间角为120°~150°,径向对应的最不利区间角为30°~60°。
3.3 不同激励方向下桥梁系统易损性分析
由前述的地震构件易损性分析可以看出,在不同地震激励方向下,各支座和桥墩的损伤状况以及破坏秩序不尽相同,故为了判定曲线梁桥的最不利地震激励方向,需要从结构构件转向结整体系统来分析损伤条件概率。文中采用宽界限法(又称一阶界限法)[21]分析桥梁系统易损性,即:将各桥梁构件看成串联体系,假定各构件之间完全相关,构件中破坏概率最大者为系统损伤概率的下限值;反之,将各桥梁构件看成并联体系,假定各构件之间完全独立,则所有构件全部失效时的概率为系统失效概率的上限值,可表示为:
式中:Psys为桥梁系统的失效概率;Pi为第i个构件发生损伤破坏的概率。
圖11给出板式橡胶支座隔震曲线梁桥各极限状态下的系统易损性曲面,其中红色表示系统易损性上界,蓝色表示不同极限状态下系统易损性下界,可以得到:
(1) 随着损伤等级的提高,采用板式橡胶支座的曲线梁桥系统地震易损性曲面呈现出不规则的形状特征,尤其以下界不规则性更加显著,其对地震激励方向的敏感性逐渐增强,这与构件易损性所得结论近似相同。
(2) 尽管构件(如桥墩)易损性对地震激励方向有较强的依赖性,但相同极限状态下桥梁系统易损性对地震激励方向的依赖性相对较弱,因此采用构件易损性代替整体桥梁系统易损性较不合理;各构件响应之间的相关性较高,因此桥梁系统易损性更加接近于易损性最大的构件,即易损性的下界;因各构件对地震激励方向的敏感性不同,且不同构件之间的相关性未知,故进行易损性分析研究时地震激励方向对桥梁易损性的影响不可忽略,否则可能导致对桥梁系统易损性的低估,从而对最终决策的合理性产生不利结果。
4 结论
为研究不同地震激励方向下隔震曲线梁桥的易损性变化规律,以某三跨曲线梁桥为研究对象,利用APDL建立采用板式橡胶支座的曲线梁桥有限元模型,选取同一地震事件中的近断层地震动进行调幅处理;考虑地震激励方向的变化,得到地震激励作用下桥梁结构构件(桥墩与支座)及系统易损性曲面,分析地震易损性变化规律所受地震激励方向的影响。得到的主要结论如下:
(1) 不同极限状态下各桥墩切向损伤条件概率均明显大于其径向,而各支座的径向与切向易损性相差不大,但总体上仍是各支座的切向易损性大于径向易损性;同时,随着损伤等级的不断提高,边墩切向与径向易损性曲线较中墩差异性更为明显,且边墩支座相较于中墩支座更容易发生损伤。
(2) 桥梁构件(桥墩与支座)切向易损性对地震激励方向表现出很强依赖性,但径向易损性对激励方向的依赖性相对较弱;随着损伤等级的提高,构件切向易损性对地震激励方向的变化更加敏感,而径向易损性对激励方向的敏感性相对较弱。
(3) 由于矩形桥墩曲线梁桥其结构特殊性,与最不利激励方向相邻的角度也应该被考虑,建议用“最不利区间角”表达,得到桥梁各桥墩与支座切向易损性对应的最不利区间角为120°~150°,径向易损性对应的最不利区间角为30°~60°。
(4) 与构件易损性不同,桥梁系统易损性对地震激励方向的依赖性相对较弱,因此采用构件易损性代替整体桥梁系统易损性较不合理,其桥梁系统易损性因各构件响应之间的相关性较高而更接近于最大的构件易损性,即易损性的下界;此外,应考虑不同地震激励方向对其地震易损性的影响,从而使得易损性分析结果更加合理,能够更加真实地反映隔震曲线梁桥的实际损伤状态。
参考文献(References)
[1] 唐伟健,王东升,张鹏颺,等.桥梁震害的历史回顾(上)[J].地震工程与工程振动,2021,41(4):70-80.
TANG Weijian,WANG Dongsheng,ZHANG Pengyang,et al.A review of the seismic damage history of bridges (Ⅰ)[J].Earthquake Engineering and Engineering Dynamics,2021,41(4):70-80.
[2] 唐伟健,王东升,张蒙等.桥梁震害的历史回顾(下)[J].地震工程与工程振动,2021,41(5):90-105.
TANG Weijian,WANG Dongsheng,ZHANG Pengyang,et al.A review of the seismic damage history of bridges (Ⅱ)[J].Earthquake Engineering and Engineering Dynamics,2021,41(5):90-105.
[3] 吴刚,王克海,宋帅,等.不同约束体系曲线梁桥震害调查及损伤模式分析[J].振动与冲击,2020,39(12):113-120,141.
WU Gang,WANG Kehai,SONG Shuai,et al.Investigation of seismic damage and analysis of damage mode of curved bridges with different restraint systems[J].Journal of Vibration and Shock,2020,39(12):113-120,141.
[4] JEON J S,DESROCHES R,KIM T,et al.Geometric parameters affecting seismic fragilities of curved multi-frame concrete box-girder bridges with integral abutments[J].Engineering Structures,2016,122:121-143.
[5] 游新,何睿華,吴刚,等.地震作用下曲线梁桥结构响应及敏感性分析[J].世界地震工程,2020,36(1):118-124.
YOU Xin,HE Ruihua,WU Gang,et al.Response analysis and sensitivity analysis of curved bridge under seismic actions[J].World Earthquake Engineering,2020,36(1):118-124.
[6] 左烨,孙广俊,金昊贵,等.曲线梁桥近断层地震响应分析[J].振动测试与诊断,2018,38(4):687-695,868.
ZUO Ye,SUN Guangjun,JIN Haogui,et al.Analysis of seismic response of curved bridge subjected to near-fault ground motion[J].Journal of Vibration,Measurement & Diagnosis,2018,38(4):687-695,868.
[7] 陈彦江,苏鹏,闫维明.带纵坡曲线梁桥地震响应试验研究[J].桥梁建设,2019,49(1):12-17.
CHEN Yanjiang,SU Peng,YAN Weiming.Experimental study on seismic response of curved girder bridge with longitudinal slope[J].Bridge Construction,2019,49(1):12-17.
[8] LI N N,XU W B,CHEN Y J,et al.Experimental research on adjacent pounding effect of midspan curved bridge with longitudinal slope[J].Engineering Structures,2019,196:109320.
[9] 李喜梅,杜永峰,母渤海.多維地震激励下曲线梁桥简化模型及最不利输入方向研究[J].地震工程学报,2020,42(2):304-310.
LI Ximei,DU Yongfeng,MU Bohai.A simplified model of,and critical angles for curved bridges under multi-dimensional earthquake excitation[J].China Earthquake Engineering Journal,2020,42(2):304-310.
[10] 冯睿为,劳天鹏,邓通发,等.基于构件合力的曲线梁桥最不利激励方向确定[J].同济大学学报(自然科学版),2019,47(3):301-308.
FENG Ruiwei,LAO Tianpeng,DENG Tongfa,et al.Resultant response-based method for assessing the critical excitation direction of horizontally curved bridges[J].Journal of Tongji University (Natural Science),2019,47(3):301-308.
[11] 梁瑞军,王浩,沈惠军,等.考虑地震动随机性的隔震曲线连续梁桥动力响应分析[J].振动工程学报,2020,33(4):834-841.
LIANG Ruijun,WANG Hao,SHEN Huijun,et al.Seismic response analysis of the isolated curved girder bridge considering the randomness of ground motions[J].Journal of Vibration Engineering,2020,33(4):834-841.
[12] 李宏男,成虎,王东升.桥梁结构地震易损性研究进展述评[J].工程力学,2018,35(9):1-16.
LI Hongnan,CHENG Hu,WANG Dongsheng.A review of advances in seismic fragility research on bridge structures[J].Engineering Mechanics,2018,35(9):1-16.
[13] MUNTASIR BILLAH A H M,SHAHRIA ALAM M.Seismic fragility assessment of highway bridges:a state-of-the-art review[J].Structure and Infrastructure Engineering,2015,11(6):804-832.
[14] TASKARI O,SEXTOS A.Multi-angle,multi-damage fragility curves for seismic assessment of bridges[J].Earthquake Engineering & Structural Dynamics,2015,44(13):2281-2301.
[15] XU T F,ZHANG Z Y,LI Y P,et al.Seismic fragility analysis of reinforced concrete piers in spatially curved urban flyover[J].Structures,2020,27:1890-1902.
[16] ABBASI M,ABEDINI M J,ZAKERI B,et al.Seismic vulnerability assessment of a Californian multi-frame curved concrete box girder viaduct using fragility curves[J].Structure and Infrastructure Engineering,2016,12(12):1585-1601.
[17] SARRAF SHIRAZI R,PEKCAN G,ITANI A.Analytical fragility curves for a class of horizontally curved box-girder bridges[J].Journal of Earthquake Engineering,2018,22(5):881-901.
[18] 中华人民共和国住房和城乡建设部,国家质量监督检验检疫总局.建筑抗震设计规范:GB 50011—2010[S].北京:中国建筑工业出版社,2010.
Ministry of Housing and Urban-Rural Development of the People's Republic of China,General Administration of Quality Supervision,Inspection and Quarantine of the People's Republic of China.Code for seismic design of buildings:GB 50011—2010[S].Beijing:China Architecture & Building Press,2010.
[19] TORBOL M,SHINOZUKA M.Effect of the angle of seismic incidence on the fragility curves of bridges[J].Earthquake Engineering & Structural Dynamics,2012,41(14):2111-2124.
[20] AMJADIAN M,AGRAWAL A K.Dynamic characteristics of horizontally curved bridges[J].Journal of Vibration and Control,2018,24(19):4465-4483.
[21] CHEN X.System fragility assessment of tall-pier bridges subjected to near-fault ground motions[J].Journal of Bridge Engineering,2020,25(3):1-12.

