强初值敏感性的一些性质及充分条件

牛应轩,汪 轶

（皖西学院数理系,安徽六安 237012）

强初值敏感性的一些性质及充分条件

牛应轩,汪 轶

（皖西学院数理系,安徽六安 237012）

设X为紧致度量空间,f:X→X为连续映射,讨论了强初值敏感性的一些性质,证明了（X,f）是强初值敏感的当且仅当其自然扩充是强初值敏感的,并给出系统（X,f）是强初值敏感的充分条件,另外证明了如果（X,f）是拓扑混合的或是区间上拓扑传递的,那么（X,f）是强初值敏感的。

强初值敏感性;初值敏感性;拓扑混合;拓扑传递

1 引言

设X为具有度量d的紧致度量空间,f:X→X为连续映射,我们称（X,f）为一个动力系统或简称为系统。本文假设X为无限的紧致度量空间,并记diam（A）为A⊂X的直径,Ac为A的余集。x∈X,ε＞0,B（x,ε）={y∈X:d（x,y）＜ε}。+和分别表示非负整数集和正整数集。对任意的n∈。我们归纳定义fn=f fn-1,f0=id为恒同映射。

（X,f）称为初值敏感的是指存在一个常数,使得对于每个非空的开集,其中都存在两个互异的点,当若干次迭代后它们两两之间的距离将大于这个给定的常数。也就是说,存在δ＞0,对任意的x∈X及ε＞0,存在y∈B（x,ε）及n∈+,使得d（fn（x）,fn（y））＞δ。初值敏感性被认为是混沌的核心概念。混沌和系统的复杂性一直是动力系统研究中的重要方向之一。关于初值敏感性的研究已经获得许多深刻的成果。对于传递系统,要么是几乎等度连续的,要么是初值敏感的[1]（P25-40）。特别地,任何极小系统,要么是等度连续的,要么是初值敏感的。极小点稠密的非极小的传递系统是初值敏感的[2]。非极小的Banach传递系统也是初值敏感的[3]。

随着研究的不断深入,研究者们给出了不同的敏感性的概念。A kin和Kloyada引入了比初值敏感性更强的概念——L i-Yorke敏感性[4]。熊金城推广了敏感性的定义引入了n初值敏感性的概念[5]。最近,有学者[6]引入了强初值敏感性的概念并研究了测度空间上的保测变换的强初值敏感性,得到了测度空间上的保测变换是强初值敏感的充分条件。

（X,f）称为强初值敏感的,如果存在δ＞0,对任意的x∈X及任意的ε＞0,存在N∈,使得对任意的n≥N,存在y∈B（x,ε）有d（fn（x）,fn（y））＞δ。δ称为（X,f）的一个强初值敏感常数。以下我们将强初值敏感简称为强敏感。

本文对拓扑动力系统（X,f）讨论了强敏感性的一些性质并得到系统（X,f）是强敏感的充分条件。证明了如果（X,f）是拓扑混合的或是区间上拓扑传递的,那么（X,f）是强敏感的。

2 强敏感性的一些性质

定理2.1 设（X,f）是具有度量d的系统。则

（1）如果（X,f）是强敏感的,那么对任意的k∈,（X,fk）是强敏感的。

（2）如果对某个k∈,（X,fk）是强敏感的,那么（X,f）是强敏感的。

证明:（1）由强敏感的定义易证。

（2）因为对某个k∈,（X,fk）是强敏感的。设δ＞0为（X,fk）的一个强敏感常数。因此,对任意的x∈X及任意的ε＞0,存在N∈,使得对任意的n≥N,存在y∈B（x,ε）有d（fnk（x）,fnk（y））＞δ。对于δ＞0,存在δ0＞0,使得当d（y1,y2）＜δ0有d（fi（y1）, fi（y2））＜δ,对i=0,1,2,…,k成立。令N′=kN,那么对任意的j≥N′存在y∈B（x,ε）使得d（fj（x）,fj（y））＞δ0。所以（X,f）是强敏感的,δ0为其一个强敏感常数。

设（X,f）和（Y,g）为两个分别具有度量d和d′的系统,π:X→Y为满足πf=gπ的连续满射,则π称为（X,f）到（Y,g）的因子映射。如果π为同胚映射,那么则称（X,f）与（Y,g）拓扑共轭。π称为半开的,如果对X的任意的非空的开集U,π（U）的内部int（π（U））非空。

由强敏感性的定义可得（X,f）是强敏感的等价地说,存在δ＞0,对X的任意的非空的开集U,存在N∈,使得对任意的n≥N,存在y1,y2∈U,有:

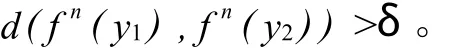
定理2.2 设（X,f）和（Y,g）为两个分别具有度量d和d′的系统,π:X→Y为（X,f）到（Y,g）的因子映射并且π为半开的。如果（Y,g）是强敏感的,那么（X,f）是强敏感的。

证明设δ＞0为（Y,g）的一个强敏感常数。那么对于δ＞0,存在δ0＞0,使得当d（x,y）＜δ0,有d′（π（x）,π（y））＜δ。对X的任意的非空的开集U,由于π为半开的,故int（π（U））≠Ø,所以存在N∈,使得对任意的n≥N,存在y1,y2∈π（U）有:

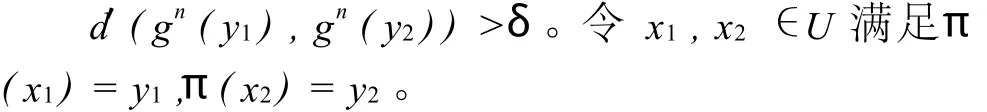
从而d′（πfn（x1）,πfn（x2））＞δ。因此我们有d （fn（x1）,fn（x2））＞δ0,所以（X,f）是强敏感的。

推论2.3 如果系统（X,f）与（Y,g）拓扑共轭的,那么（X,f）是强敏感的当且仅当（Y,g）是强敏感的。

设（X,f）为具有度量d的系统且f是满射,令

3 强敏感性的充分条件

定理3.1 如果动力系统（X,f）是拓扑混合的,那么（X,f）是强敏感的。

由定理2.1的（2）及定理3.1,我们有:

推论3.2 如果存在k∈,使得（X,fk）是拓扑混合的,则（X,f）是强敏感的。

注记3.3 称系统（X,f）是一致刚性的,如果存在正整数序列有fni一致收敛于恒同映射。显然,一致刚性系统不是强敏感的。文献[8]给出极小的一致刚性的弱混合系统,因此存在弱混合系统甚至极小的弱混合系统不是强敏感的。

对于区间上的一维动力系统,我们有:

定理3.4 设I=[0,1]是闭区间,f:I→I连续,如果f是拓扑传递的,（I,f）则是强敏感的。

为了证明定理3.4,我们需要下面的引理。

引理3.5（[9]）设I=[0,1]是闭区间,f:I→I连续,则f是拓扑传递的当且仅当下列条件之一成立:

（1）f是拓扑混合的;

（2）存在不动点e∈（0,1）,使得f（[0,e]）=[e,1],f（[e,1]）=[0,e]且f2|[0,e]与f2|[e,1]都是拓扑混合的。

定理3.4的证明设f是拓扑传递的,如果引理3.5中的（1）成立,则由定理3.1可得（I,f）是强敏感的。

[1]EAkin,J Auslander and KBerg.When is a Transitive Map chaotic?[A].V.Bergelson,P.March,J.Rosenblatt.Convergence in Ergodic Theo ry and Probability（Columbus, OH,1993）（Ohio University Math.Res.Inst.Pub.,5） [C].Berlin,New York:de Gruter,1996.

[2]Glasner E,Weiss B.Sensitive Dependence on Initial Conditions[J].Nonlinearity,1993,（6）:1067-1075.

[3]Huang W,Ye X.An Explicit Scattering,Non-weakly Mixing Example and Weak Disjointness[J].Nonlinearity, 2002,15:1-14.

[4]Akin E,Kolyada S.Li-Yorke Sensitivity[J].Nonlinearity,2003,16:1421-1433.

[5]熊金城.拓扑传递系统中的混沌[J].中国科学A辑,2005, 35（1）:302-311.

[6]Christophe A,Gerard B,Benoit C.Chaotic Properties on a Probability Space[J].J.Math.Anal.Appl.,2002,266（2）: 420-431.

[7]Kolyada S,Snoha L.Noninvertible Minimal Maps[J]. Fund.Math.,2001,168（2）:141-163.

[8]Glasner S,Maon D.Rigidity in Topological Dynamics[J]. Ergodic Theo ry and Dynamical Systems,1989,9（2）:309 -320.

[9]汪火云,熊金城.拓扑遍历映射的一些性质[J],数学学报, 2004,47（5）:859-866.

Some Properties and Sufficient Conditions on the Strong Sensitivity to Initial Conditions

NIU Ying-xuan,WANG Yi

（Dept.of Math.and Phys.,West Anhui University,L u’an237012,China）

LetXbe a compactmetric space andf:X→Xcontinuous.In this paper,some propertiesof the strongly sensitive dependence on initial conditions are discussed,it is obtained that（X,f）is strongly sensitive if and only if so is its natural extension,and some sufficient conditions for（X,f）to be strongly sensitive are obtained.What’s more,it is show n that if（X,f）is topological mixing or topologically transitive on the interval,then（X,f）is strongly sensitive.

strongly sensitive dependence on initial conditions;sensitive dependence on initial conditions;topological mixing;topologically transitive

O189.11

A

1009-9735（2010）02-0001-03

2010-03-04

项目资金:安徽省教育厅自然科学研究项目（KJ2007B123）;皖西学院自然科学青年项目（WXQZ0602）。

牛应轩（1962-）,男,安徽六安人,教授,研究方向:动力系统与遍历理论。