基于AM-MCMC算法和Nash模型的概率洪水预报*

邢贞相 芮孝芳 冯 杰

(东北农业大学水利与建筑学院1) 哈尔滨 150030)

(东北农业大学农业工程博士后科研流动站2) 哈尔滨 150030)

(河海大学水文水资源学院3) 南京 210098)

BFS(贝叶斯概率预报系统)是一个可与任一确定性水文模型协作进行概率水文预报的通用理论框架[1],其理论基础是贝叶斯公式.Krzysztofowicz相继提出了线性正态假设、亚高斯转换、概率定量降雨预报和概率河流水位预报的贝叶斯系统等[2],推动了BFS的研究进展.国内,张洪刚采用平稳序列线性AR模型与线性扰动模型(LPM)分别描述先验分布与似然函数,在一定程序上降低了贝叶斯求解的复杂度[3];李向阳等采用神经网络模型来描述先验分布与似然函数,进一步降低了贝叶斯求解过程的复杂程度[4].王建平等[5]将贝叶斯理论用于水质模型的参数识别问题,对复杂环境模型参数的不确定性进行了研究.贝叶斯理论还是贝叶斯网络模型的基础,它是一种不确定性知识的表达与推理模型,在建筑、经济,环境等领域均有广泛应用[6].本文尝试将贝叶斯理论与自适应马尔可夫链蒙特卡罗算法相结合来研究Nash模型参数的不确定性,并将其用于洪水概率预报.

1 BFS的基本原理

BFS的理论依据就是下列贝叶斯公式

式中:π(θ|x)为参数的后验密度,它是在样本 x给定条件下,参数 θ的条件分布;π(θ)为θ的先验分布;p(x|θ)为似然函数;Θ为θ的积分区间.

π(θ|x)集中了总体、样本和先验等3种信息中有关θ的信息,是排除一切与θ无关的信息后所得的结果.基于后验分布 π(θ|x)对 θ进行统计推断将更为有效、合理,称之为贝叶斯统计推断.

当参数的先验密度与似然函数形式确定后,为获得式(1)的后验密度解析式还需求得其右端分母的积分,而参数θ的积分区间只能靠实测资料估计,无法获得其真实的区间,所以,很难求得式(1)的解析式,为此,本文采用数值解法来获得后验密度,即用马尔可夫链蒙特卡罗随机模拟的方法求其数值解.

作为随机模拟方法的马尔可夫链蒙特卡罗(MCMC)方法的关键是如何选择推荐分布(转移密度)使采样更加有效.常用的采样方法有Metropolis-Hastings算法、吉布斯(Gibbs)采样和Adapative-Metropolis(AM)算法[7].这 3种方法中只有AM算法的不依赖于事先确定的推荐分布且可并行运算,收敛速度快,故本文采用此算法.关于AM算法的具体过程和收敛判断准则及性能测试参见文献[8-9].

2 Nash模型参数的不确定性

本文利用AM-MCMC算法将Nash模型参数k,n分两种情况研究其不确定性:(1)将参数k视为随机的,而参数n视为确定性的;(2)将2参数均视为随机的.由于第一种情况是第二种情况的特例,故本文只介绍第二种情况的具体过程.Nash模型的输入,即地面净雨的计算采用斜线分割法.

选取长江三峡沿渡河流域作为研究区域,共有30场洪水实测资料.该流域位于长江三峡地区,其水系流经神农架林区巴东县.流域内降水丰沛,流域多年平降雨量为1 337 mm,全年雨量以5～9月最多,约占全年68%.流域内最大年降水量为2 448.2 mm,最小年降雨量为808.4 mm.

沿渡河流域面积601 km2,流域坡度较大,平均坡度为0.287%,高程垂直落差达2 800 m,山高坡陡,人类活动影响较小,流域内耕地面积占流域面积的10%左右,森林覆盖率在70%以上.由于流域内植被覆盖良好,地表径流中含沙量不大,除洪水期含沙量有所增大外,其余时间河水清澈.

2.1 先验分布的确定

1)参数n的先验分布的确定 假定其服从正态分布,根据地貌学的方法求得沿渡河流域的Nash模型参数n=3,可认为是其分布的均值,设其先验方差为均值的10%,则得n的先验分布为n～N(3,0.3).

2)参数k先验分布的确定 首先率定参数 ,选用该流域1981～1987年间28场洪水资料来率定参数k值.为保证计算精度,取计算时段长为1 h.为避免异参同效现象的影响,令n=3保持不变,单独率定k,方法采用矩法-优选法.根据各场洪水k的率定结果求得k取值范围为[1,1.96],其均值为1.19,方差为0.09,并假定其服从正态分布,即得k的先验分布为k～N(1.19,0.09).

2.2 似然函数的确定

由于有28场洪水资料参与率定,故采用多观测拟合优度的似然函数

式中:Q为流量;σei为第i个观测与模型预报的误差系列的标准差;N为实测序列的个数,本文为N=28;其余符号意义同前.

2.3 AM-MCMC算法初始条件

AM-MCMC算法初始条件:初始协方差取为对角阵,初始化迭代次数为2 000,初始化阶段次数为2 000,每次采样为10 000次,算法并行运行5次,这样共将取样(10 000-2 000)×5=40 000组(n,k)以用于沿渡河流域Nash模型参数的不确定性研究.

2.4 Nash模型参数不确定性分析

AM-MCMC运算结束后,根据所抽40 000个样本,统计得出Nash模型参数的边缘后验密度分别为 k～N(2.03,0.09)(见图 1),n～N(2.61,0.10)(见图2),从图1,图2可见k和n的后验边缘密度均近似服从正态分布,通过Kolmogorov-Smirnov假设检验在显著性水平为0.05时接受各自后验分布为正态分布的原假设.图3给出了2参数的后验均值迭代迹线、图4给出了2参数的后验方差迭代迹线,从2图中看出自第2 000次迭代后2参数的后验均值、后验方差均趋于稳定,说明所抽样本已具有总体样本的统计特性.图5给出了两参数的联合后验概率密度,从图中看出两参数的联合分布只有一个极值,其坐标为两参数的后验均值.图6给出了两参数样本的散点图,由图可见,n与k之间存在着明显的相关关系.

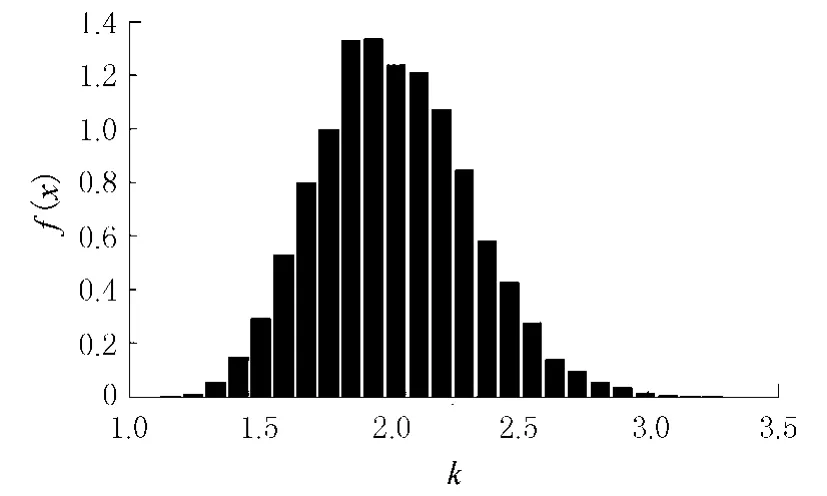
图1 参数k的后验边缘密度

图2 参数n的后验边缘密度

图3 参数n,k的后验均值迭代迹线

图6 参数n与k的散点图

3 Nash模型的降雨径流概率预报

芮孝芳[10]指出,产生水文模型的“异参同效”这一现象的原因至少有:目标函数是多极值的;模型中包含的参数之间存在相互补偿作用;模型参数具有随机性.图1和图2虽给出了Nash模型两参数的各自后验边缘密度,但却无法避免存在的“异参同效”现象,在实际水文预报时,真正有意义的是两个参数的组合,而不是单个参数.为此,本文随机选取AM-MCMC算法收敛后的10 000个参数组样本分别对沿渡流域洪水进行模拟,使某一场洪水的每个时段对应所选取的不同参数组生成10 000个流量数值.用这些数据作为样本来研究各时刻流量的统计特性,即可求得各时刻(包括洪峰时刻)流量的概率分布,其均值和方差及指定概率的置信区间.在作业预报时可采用每一时刻的预报流量样本的均值作为其预报值.

表1中只给出了本文算法对沿渡河流域6场洪水(其他洪水限于篇幅未列出)的峰值概率预报及其80%的置信区间.在表1中,同时给出了当参数k为随机而n为确定时的相应场次洪水的峰值预报结果(研究方案1为仅参数k为随机的情况,方案2为参数k和n均为随机的情况).通过对该流域30(其中的28场为参数率定过程所用过的洪水作为校核样本,另810824和870827两场为预报样本)场洪水的预报结果可知,其中洪峰预报误差在20%以内的场次占总体的77%,洪峰误差小于10%的场次占总体的60%.平均洪峰误差为12.6%,所有洪峰滞时均在3 h以内,平均洪峰滞时为1.3,所有确定性系数均大于0.70,平均确定性系数为0.86;与单一参数k为随机的模型预报结果相比,大部分洪水的洪峰误差有所降低,确定性系数稍有提高;平均确定性系数相当,而平均洪峰滞时降低了58%.这说明了Nash模型的确存在着较强的“异参同效”现象.两场预报洪水的计算精度也较高.与仅k为随机的情况下的预报结果相比,2参数均为随机的计算洪峰均方差和80%的置信区间均有所增大,这说明预报结果的不确定性增大了,这也正是由于增加了参数n的不确定性所致.综述之,模型参数的不确定性对确定性系数影响较小,对洪峰误差、洪峰滞时和置信区间影响较大.

图7绘出了洪号为810714 a)和810824 b)2场洪水的洪峰后验密度直方图及其极大似然估计的理论正态密度曲线,据图看出各洪峰的密度直方图与估计的理论正态密度曲线吻合较好.图8绘出了这2场洪水的80%的置信区间与实测洪水的比较,据图看出每场洪水的实测流量几乎都包括在80%的置信区间内.图9给出了这2场洪水基于AM-MCMC算法的Nash模型2参数均为随机的BFS预报均值过程与实测过程的比较.由图9可见,2场洪水的拟合精度都很高.

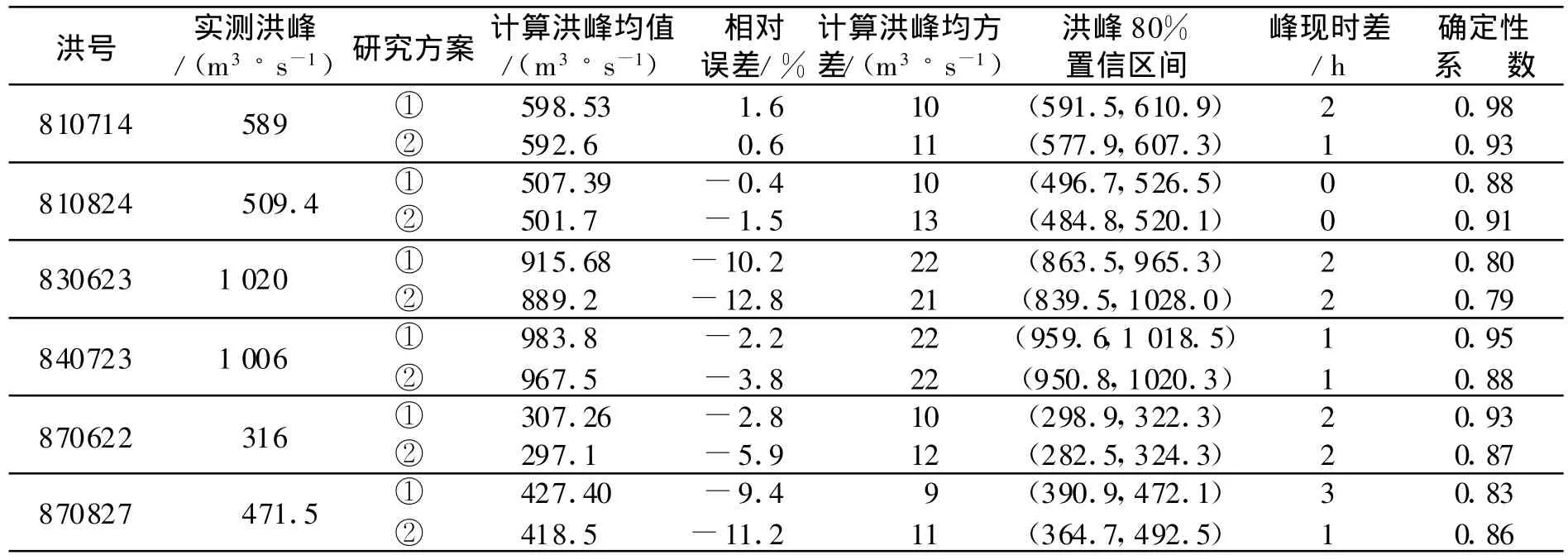
表1 沿渡河流域参数随机的Nash模型的概率洪水预报成果表

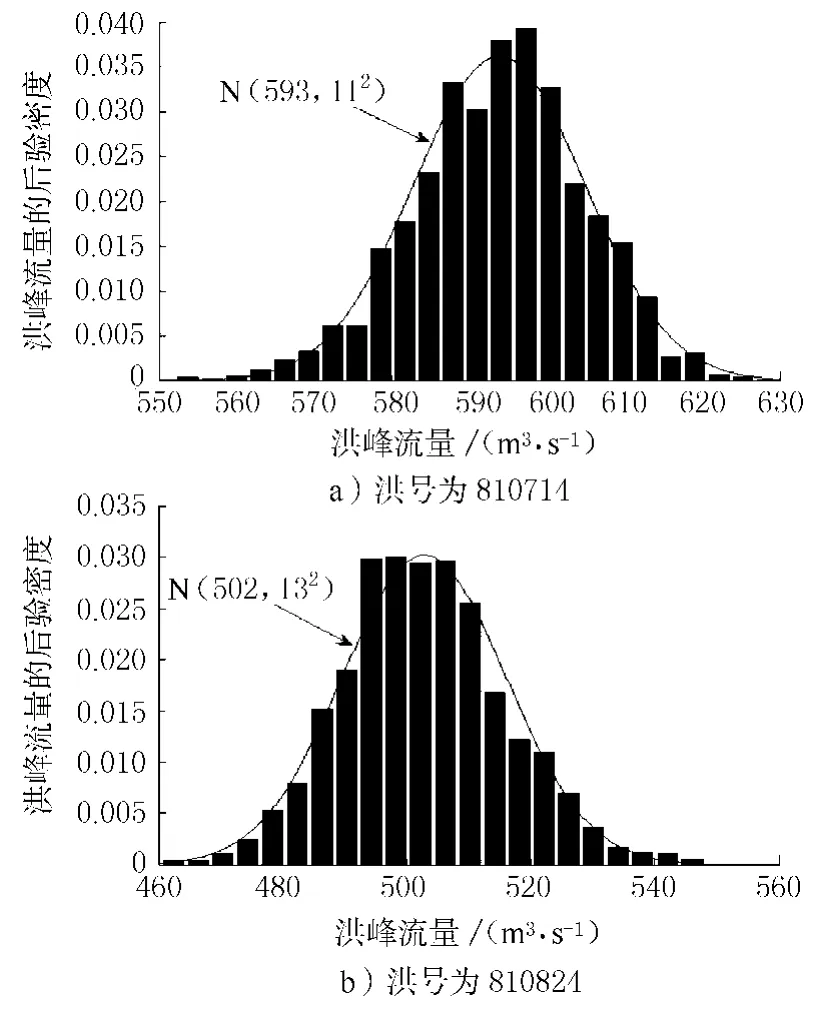
图7 洪峰后验密度直方图及其理论密度曲线

图8 概率预报的80%置信区间与实测过程比较

图9 概率预报过程与实测过程比较

4 结 论

1)贝叶斯概率预报系统可与任一复杂的确定性水文模型协同工作,而无需附加任何假设,是制定概率水文预报的通用理论框架.

2)AM算法采用并行抽样,速度快,无需事先指定MCMC算法的推荐分布,且考虑所抽历史样本的信息,能准确地获得指定参数的总体分布特征,具有算法上的优越性.

3)AM-MCMC算法能较好获取Nash模型参数k,n的后验分布特征,Nash模型的两个参数均存在较强的不确定性,沿渡河流域两参数均近似服从正态分布.使模型的应用不再受有限实测资料的制约.

4)贝叶斯概率洪水预报不仅可给出洪水各时刻的流量,而且能借助给出的各时刻的流量方差考虑洪水预报的不确定性,便于在实际应用中估计各种防洪决策的风险.

[1]Krzysztofowicz R.Bayesian theory of probabilistic via deterministic hydrologic model[J],Water Resour.Res.,1999,35(9):2 739-2 750.

[2]Krzysztofowicz R,Maranzano C J.Hydrologci uncertainty processor for probabilistic stage transition forecasting[J].Journal of Hydrology,2004,293(1-4):57-73.

[3]张洪刚.贝叶斯概率水文预报系统及其应用研究[D].武汉:武汉大学水利水电学院,2006.

[4]李向阳,程春田,林剑艺.基于BP网络的贝叶斯概率水文预报模型[J].水利学报,2006,37(3):354-359.

[5]王建平,程声通,贾海峰.基于MCMC法的水质模型参数不确定性研究[J].环境科学,2006,27(1):24-30.

[6]陈小佳,沈成武.既有桥梁的贝叶斯网络评估方法.武汉理工大学学报:交通科学与工程版,2006,30(1):132-135.

[7]Haario H,Saksman E,Tamminen J.An adaptive metropolis algorithm[J].Bernoulli,2001,7(2):223-242.

[8]Gelman A,Carlin J B,Stren H S,et al.Bayesian data analysis[M].London:Chapmann and Hall,1995.

[9]Gelman A,Rubin D B.Inference from iterative simulation using multiple sequences[J].Statistics Science,1992,7(4):457-511.