断裂力学中奇异积分方程的数值求解方法

陈梦成

(华东交通大学土木建筑学院,江西南昌330013)

在数学模型上,很多断裂力学问题的求解大都可归结为奇异积分方程的求解[1-3],如裂纹的反平面冲击响应问题和SH波散射问题均可归结为求第一类Cauchy奇异积分方程[4];而平面冲击响应和P波散射问题可归结为求解第二类Cauchy奇异积分方程;此外,在研究某些二维和三维裂纹问题时,还会导出超奇异积分方程[5-10]。

求解奇异积分方程的传统方法[11-15]是用方程本身的特征算子的相联算子作为正则化算子,对奇异积分方程进行正则化,消除积分核的奇异性,化为Fredholm积分方程求解。早在上世纪50年代,Muskhelishvili[11]对奇异积分方程的解析解的理论进行了系统的研究。但是,一般情况下,奇异积分方程的解析解很难得到。因而,用数值方法解奇异积分方程受到广泛关注。

Karpenko[16]较早开始探索奇异积分方程的直接数值解法。Erdogan&Gupta[17-18]系统研究了利用Chebyshev多项式和Jacobi多项式求解第一类和第二类Cauchy型奇异积分方程的数值解法。Krenk[19-20]不仅深入研究Gauss-Chebyshev求积公式,更重要的是将正常积分的Gauss-Jacobi求积公式推广到奇异积分,并用于求解第二类Cauchy奇异积分方程。Ioakimidis&Theocaris[21]证明了由Gauss-Chebyshev求积公式得到的线性代数方程组与由正则化方法得到的线性代数方程组是一致的。Theocaris&Ioakimidis[22]将Lobatto-Chebyshev求积公式用于奇异积分方程,改善了Gauss-Chebyshev求积公式。Gerasoulis[23]提出了分片连续函数方法,在局部用低阶连续函数去模拟实际解,直接求解配置点的函数值。Miller和Keer[24]对分片连续函数法作了改进,并用于求解第二类奇异积分方程。Russel,Thomas和Sun[25]对分片连续函数法在提高求积效率和加速收敛等细节方面进一步做了改进。

国内对奇异积分方程的数值解法的研究起步比较晚,但是发展很快,特别是在数值方法的理论分析方面,我国学者作出了一定的贡献。路见可[26]在研究了各类Chebyshev求积公式之后,首次指出了奇异积分求积与经典Gauss求积这两者之间的联系,提出了具有普遍意义的分离奇点的方法,通过分离奇点将奇异积分的求积问题归纳为相应的经典求积问题。之后,路见可又用基于密度函数变换的方法研究了闭形式下的求积公式。杜金元[27-32]建立了一般情形下的HG(Hunter-Gauss)型求积公式,讨论了在一般情况下的闭形式的求积公式即HM(Hunter-Markov)型求积公式。杜金元又将节点仅仅取在Markov节点上,提出了另一种类型的求积公式,称为PEM(Paget-Elliott-Markov)型求积公式。对于封闭曲线上奇异积分方程,王小林[33,34]等采用了样条逼近解法。

在超奇异积分方程方面,在20世纪早期,学者Hadamard[39]首次提出了“有限部积分”(finite-part integerals)的概念用来求解超奇异积分。超奇异积分方程相对于Cauchy奇异积分方程更难以求得其解析解,因此,学者们把目光放在其数值求解上。在上世纪70年代,Kutt[40]建立了超奇异积分方程的求积公式进行数值计算。超奇异积分方程方法是由希腊学者Ioakimidis[5]首先引入断裂力学的。他使用了有限部积分的概念的方法,证明了受法向载荷作用的二维与三维I型裂纹可以推导出奇异积分方程(组),并指出这些方程组可以用Kutt建立的超奇异积分方程的求积公式进行数值计算。Erdogan[41]将超奇异积分方程方法用于平面和反平面断裂力学问题,并系统地为其建立了数值解法。超奇异积分方程方法可以获得主值型奇异积分方程方法无法获得的高精度结果。Takauda等用超奇异积分方程方法数值求解了I型圆形裂纹问题,得到的数值结果比Bui用主值型奇异积分方程方法求得的结果要好的多。国内学者汤任基和秦太验等[7-10,42]利用边界积分方程方法,统一导出了三维断裂力学中柯西主值型和超奇异型的两类奇异积分方程,并使用有限部积分与边界元结合的方法进行数值求解。乐金朝[44],杜云海等[45-47]将双材料平面裂纹问题求解归结为超奇异积分方程求解,并采用多项式开法进行求解。陈梦成等[48-53]使用超奇异积分方程方法对两相材料三维界面断裂力学问题、横观各向同性材料三维断裂力学问题和压电材料三维断裂力学问题进行了求解,并系统地为其建立了多项式和有限元解法。秦太验等[54-56]将超奇异积分方程方法应用于磁电热弹断裂力学问题。

本文对现有的数值方法进行分类总结,对各类方法的优缺点、数值精度、计算效率和适用范围进行讨论,并通过实际算例的数值结果作对比分析。最后,对奇异积分方程数值求解的未来研究方向作了讨论。

1 奇异积分方程基本理论

Muskhelishvili[11]对奇异积分方程的基本理论进行了系统研究,为奇异积分方程的解析求解和数值求解奠定了基础。

设L是一分段光滑曲线(开口或闭口),φ(x)在L上满足Höder条件。考虑下列积分

可以分为以下几种情况:

①当n≤0时,令κ=-n,(1)式可以整理得到

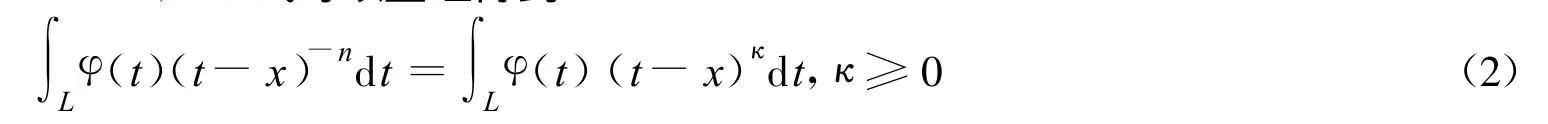
这个积分可以利用传统的数值积分进行计算。

②当0＜n＜1时,这个积分为弱奇异积分。一般来说,弱奇异积分是收敛的。通过对变量进行代换,就可消除积分核的奇异性。例如:对于下面这个积分,令 x=y2,则有

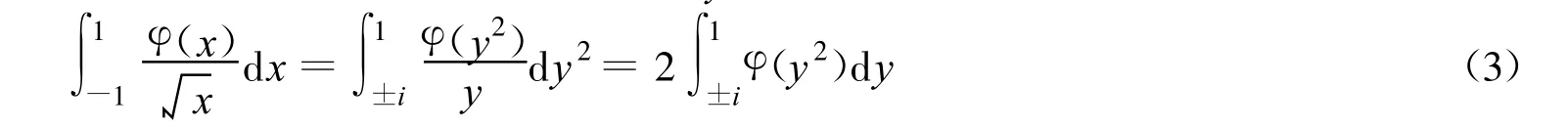
这个积分为奇异积分。一般地,Cauchy奇异积分是发散的,但当 φ(x)在L上满足Höder条件时,这个积分在主值意义下是存在的。即设 x为L上的一个内点,以x为中心,作充分小半径ε的圆周,分别在x的两边交L 于x′,x″两点。

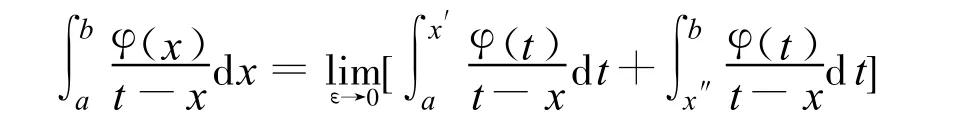
若上式极限存在,则记为

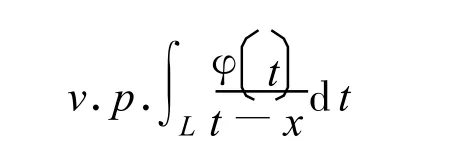
以后遇到上面形式的积分时,恒理解为Cauchy主值积分,不再一一声明。

④当n＞1时,(1)式为

这个积分为高阶奇异积分。高阶奇异积分通常是发散的,即使在柯西主值意义下也是发散的。因此定义“有限部积分”(finite-part integrals)作为高阶奇异积分的积分值。有限部积分是在计算高阶奇异积分时,舍弃积分发散的部分,保留积分收敛的部分。对于非奇异积分和弱奇异积分方程的数值求解有很多常义积分方法可以利用,本文仅阐述已有的一些Cauchy奇异积分与超奇异积分的数值求解方法。

2 Cauchy奇异积分方程的数值解法

2.1 解的一般形式

Cauchy奇异积分方程的一般形式为[35]

其中:φ(x),f(x),k(x,t)在(-1,1)内满足Höder条件;a,b为实常数或复常数。

当a=0时,称(6)式为第一类Cauchy奇异积分方程;当a≠0时,称(6)式为第二类Cauchy奇异积分方程。根据Plemelj公式

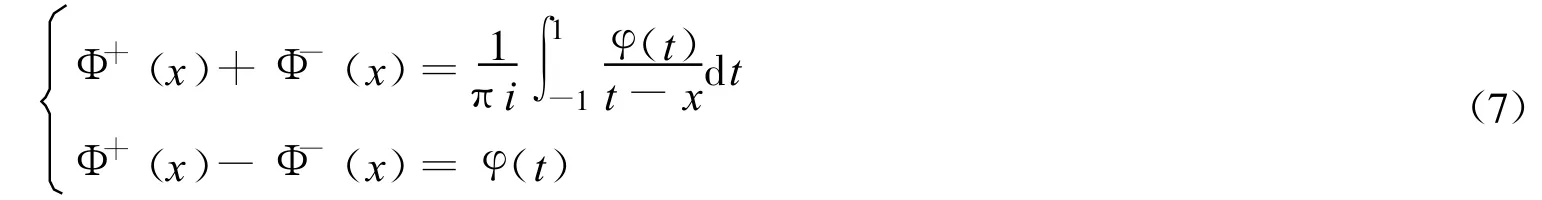
其中:Φ+(x),Φ-(x)是解析函数。

在开口或闭口边界L的左右边值,可将(6)式化成如下非齐次Riemann-Hilbert问题

求解(9)式时,应先求解对应的齐次Riemann-Hilbert问题

(10)式可以进一步化成跳跃问题

令

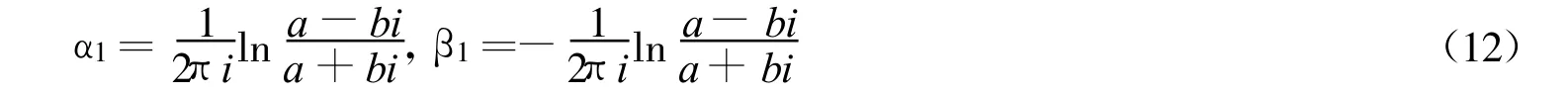
则上述问题的特解为

定义奇异积分方程(6)式的基本解为

其中:N,M由函数φ(x)在端点的性质决定。定义κ=-(N+M),则κ的取值与端点的性质的关系为

①当κ=1时,函数φ(x)在两个端点均无界,但有可积的奇异性,为保证解的唯一性,φ(x)应满足附加条件:

为保证函数φ(x)在端点存在可积奇异性,要求-1＜Re(α)＜1,-1＜Re(β)＜1。从而,奇异积分方程的一般解可以写成

其中:g(x)为区间(-1,1)内的有界连续函数。

2.2 Jacobi多项式展开法

Erdogan[17]提出了利用Jacobi多项式级数展开待求的未知函数的方法。其实质是用一组正交多项式之和表示的连续函数作为最终解。

将连续函数按Jacobi多项式级数展开,则奇异积分方程的解可以写为

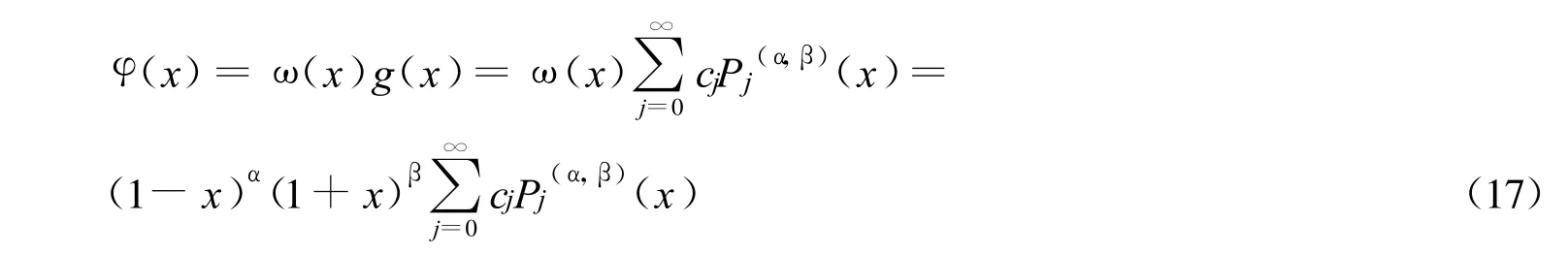
根据精度的需要,一般取级数的前N项和作为无穷级数的和。其中cj为展开级数。

将(17)式代入(6)式,利用公式[35],得到

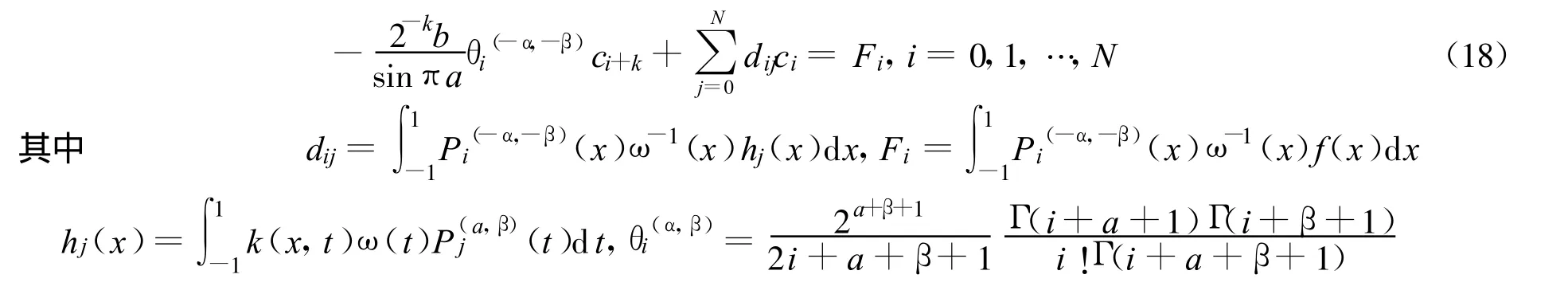
且以上积分均为常义积分,可以利用Gauss求积公式计算出其数值积分值。

①当κ=1时,方程组(18)有N+1个方程,N+2个未知数,故需要补充1个方程,由平衡条件

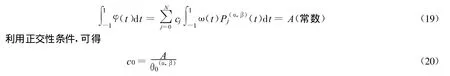
其它cj(j=0,1,…,N)可以由方程(18)确定。

②当κ=0时,方程组(18)有N+1个未知数,故其有唯一解。

③当κ=-1时,令c-1=0,此时方程组(18)有N+1个方程,N+1个未知数,可解性条件已经包含在方程组中。考虑到 P0(-α,-β)(x)=1,从而 κ=0对应的方程就是可解性条件。

Jacobi多项式展开法就是将待求的未知函数按Jacobi多项式级数形式展开,并利用Jacobi多项式的正交性质,将Cauchy奇异积分方程转化成关于展开系数cn为未知数的代数方程组。通过求解线性代数方程组,确定cn后,代入到(17)式,可以得到未知函数有限项的近似结果。这种方法对于第一类与第二类Cauchy奇异积分方程均适用。对于第一类奇异积分方程组,只需要在上述推导过程中令 α=0即可。

2.3 Chebyshev多项式展开法

Erdogan和Gupta[18]系统地阐述了利用第一类与第二类Chebyshev多项式求解第一类Cauchy型奇异积分方程的数值方法。根据不同的端点类型,分别用不同的Chebyshev多项式进行展开。记Tj(t)为阶数为j的第一类Chebyshev多项式,Uj(t)为阶数为j的第二类Chebyshev多项式。

①当 κ=1时,令

则(21)式可以化简得到

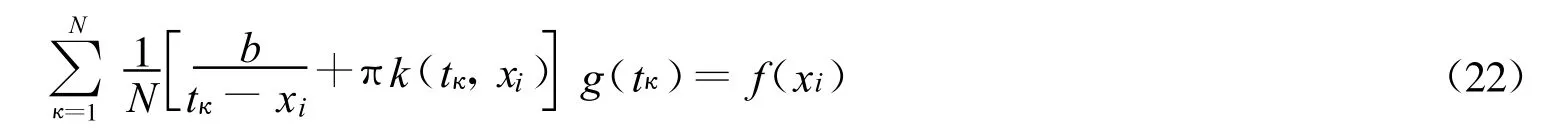
得到关于 g(tκ)的线性方程组。

补充平衡条件

②当 κ=0时,令

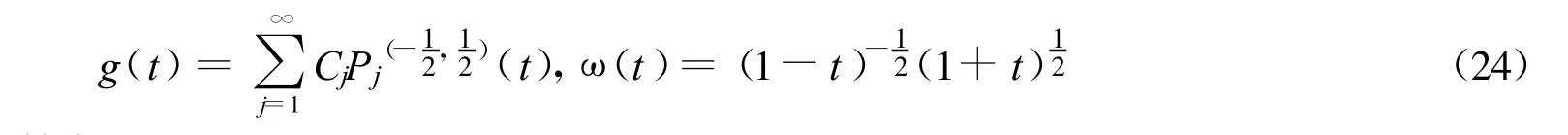
则(21)式可以化简为

或

则(21)式可以化简为

可见,κ=0的两种求积公式是完全不同的,但它们的离散方程均为已封闭定解。

③当 κ=-1时,令j=1

则(21)式可以化简得到

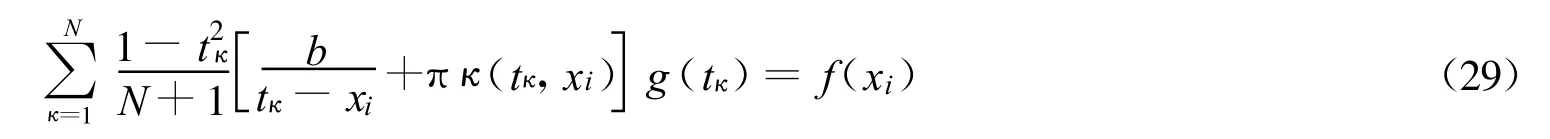
其中

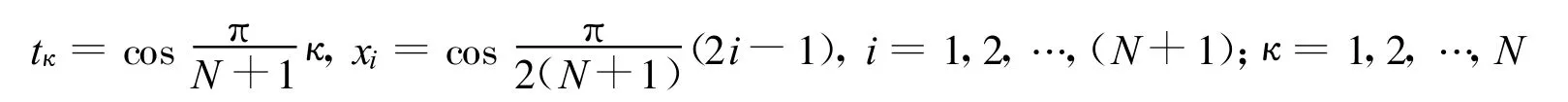
方程组(29)有N个未知数,N+1个方程。显然,需要舍去一个方程。一般舍去这个方程。表示取整。

这样即可求出第一类Cauchy奇异积分方程的解函数在积分区间上若干积分点的函数值。积分点以外的函数值,可以通过插值法实现。所以,求积公式的阶次越高,产生的积分点就越多,则所得的数值结果就越逼近真实解。

2.4 Gauss积分公式法

Krent[19-20]不仅深入研究了Gauss-Chebyshev求积公式用于求解第一类奇异积分方程,而且将常义积

分的Gauss-Jacobi求积公式推广到奇异积分,用于求解第二类奇异积分方程。

常义Gauss-Jacobi求积公式为

将Gauss-Jacobi求积公式推广到奇异积分得到

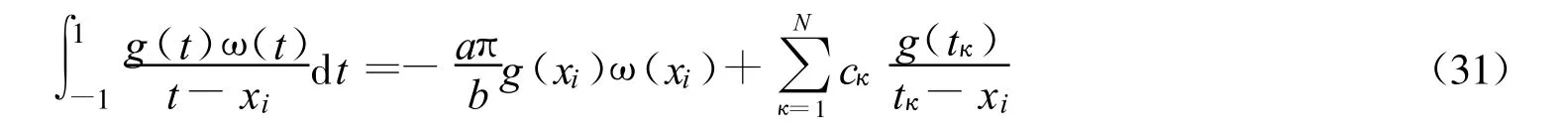
利用(30)式代入(21)式得到关于积分点函数值g(tk)的代数方程组才能构成唯一解。

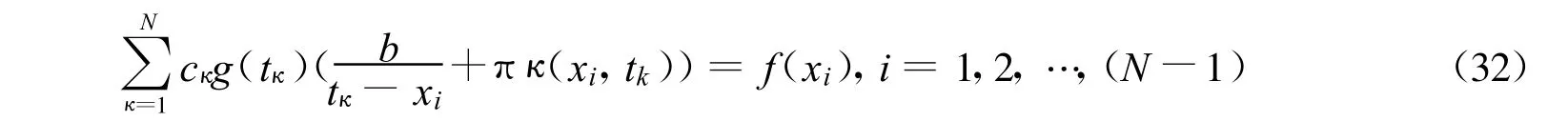
②当κ=0时,方程组(32)有N个方程,N个未知数,正好构成唯一解。

③当κ=-1时,方程组(32)有N+1个方程,N个未知数。显然,需要舍去一个多余方程,才能构成唯一解。

Gauss求积公式将常义积分的Gauss-Chebyshev求积公式和Gauss-Jacobi求积公式推广到奇异积分,导致出现两组点,一组为配置点。代数方程组的未知量是积分点上的函数值。不同于多项式展开法,求积公式法不含任何积分运算,计算工作量相对于多项式法小的多,而且推广到奇异积分的Gauss型求积公式具有2N阶的数值精度。

Gauss求积公式法和Chebyshev多项式展开法有一定的相似性,当时,两种方法相同。可以说,Gauss求积公式法是Chebyshev多项式展开法的一种推广。但是,这两种方法都存在一个缺点,就是在求两个端点附近函数值的时候,需要通过插值法来计算,而这些函数值往往在端点处变化十分剧烈,因此,通过插值法计算端点的值,误差也会比较大。Gauss求积公式法在计算不同次Jacobi多项式零点时,就已经引入了不小的误差。

2.5 Lobatto-Chebyshev求积公式

Ioakimidis和Theocaris进一步将Lobatto-Chebyshev求积公式用于奇异积分,从而将积分端点纳入积分配置点,改善了Gauss-Chebyshev求积公式不能直接计算端点函数值的缺点[22]。

对于第一类奇异积分方程,令

将(39)式代入(21)式得到

其中

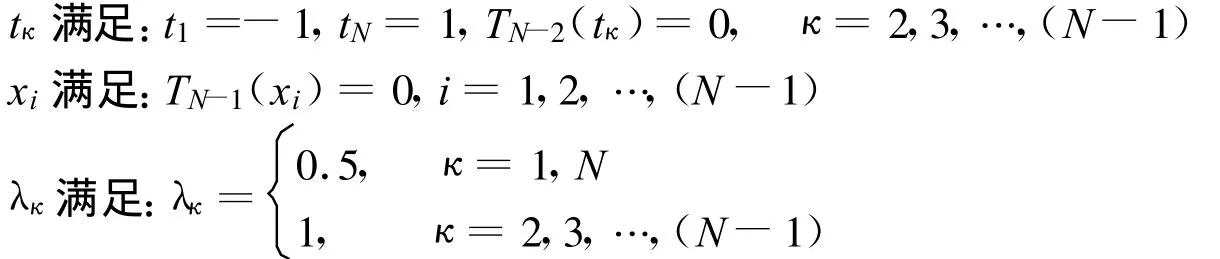
上式中方程个数为N-1,未知数g(tκ)的个数为N,要得到唯一解,应补充附加条件:

Gauss求积公式的积分点不包含端点,因而,当要求计算端点函数值时,往往需要向外插值,引入很大的误差。Lobatto-Chebyshev求积公式的积分点包含有端点,因而,在计算端点函数值时,不需要外插,避免了误差的引入。端点函数值因与裂纹尖端应力强度因子的计算有关,往往需要精确计算。因此,在这方面,Lobatto-Chebyshev求积公式法优于Gauss求积公式法。但Lobatto-Chebyshev求积公式应用于奇异积分,精度是2N-2阶,比Gauss求积公式的精度低,而且这种方法只适用于第一类奇异积分方程。

2.6 分片连续函数法

Gerasoulis[23]提出分片连续函数法,完全不同于以前的多项式展开方法和求积公式法,而是从局部出发用分片低阶连续函数去模拟实际解,直接求解配置点的函数值。该方法的原理是将区间(-1,1)化成N个子区间,在子区间上用低阶连续函数来逼近真实解。同样,在分片函数法中也有一组积分点,一组配置点,它们都是可自由确定的。积分点和配置点设置的灵活性使这一方法在某些具体问题中具有其他方法不可替代的优势。例如,当f(x)在(-1,1)内局部剧烈变化时,可以通过在相应f(x)剧烈变化的区域设置密集的积分点和配置点,来实现局部网格细化,既提高数值逼近精度,又不过分增加计算工作量。分片连续函数法包含大量的积分运算,计算工作量比求积公式法要大,这是换取积分点和配置点可以灵活设置而付出的代价[35].

2.7 数值算例

(1)算例1

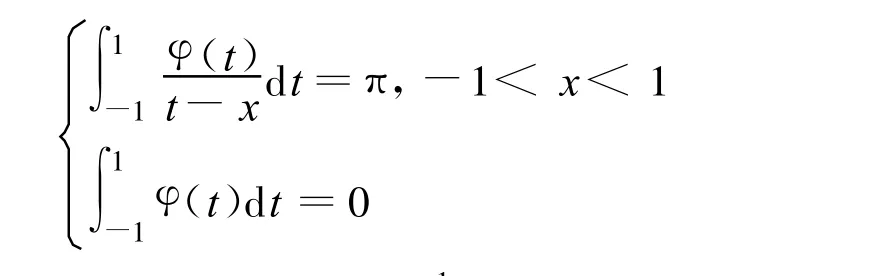
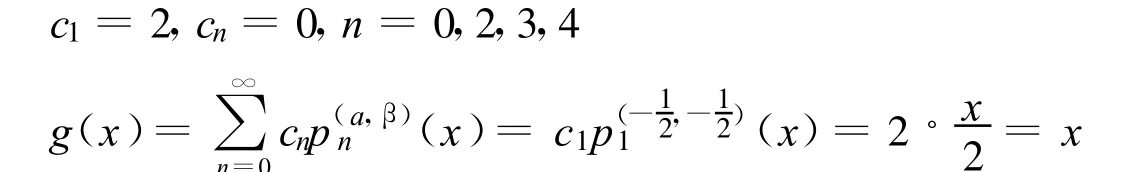
表1是用Jacobi多项式展开法、Lobatto-Chebyshev求积公式法、Gauss-Jacobi积分公式法和分片连续函数法分别计算所得到的数值结果。

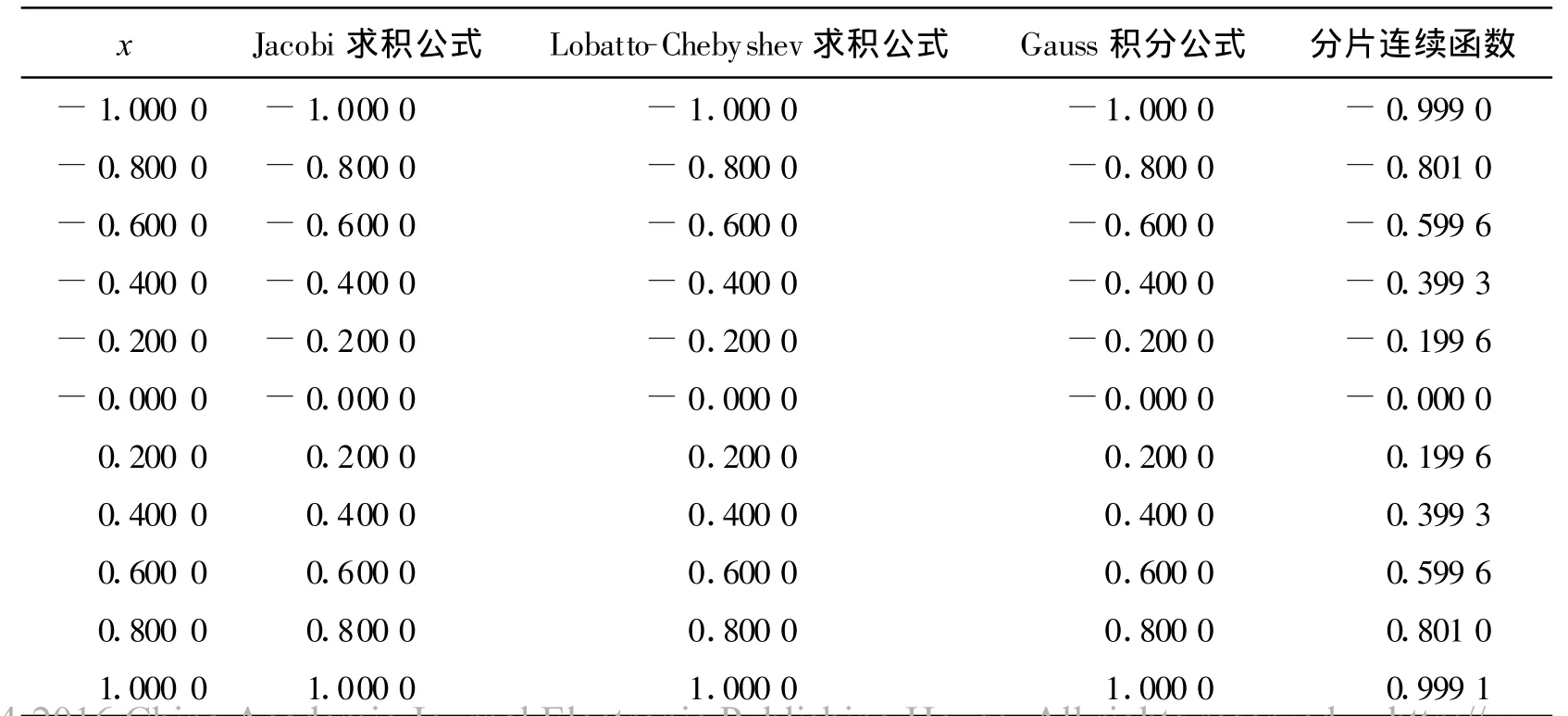
表1 四种数值解法g(x)结果比较

评价:这四种方法,对于简单的Cauchy奇异积分方程都是适用的,尤其是Jacobi多项式展开法得到的结果是解析的,并不需要进行插值计算(-1,1)区间内其他点的函数值,精确度很高;其它三种方法都是通过插值计算得到这些点的函数值,也很接近精确值。若需要计算其他点的函数值,只要以这些点为基点进行插值即可。Gauss积分公式法的端点的函数值式通过插值得到的。

(2)算例2[19]

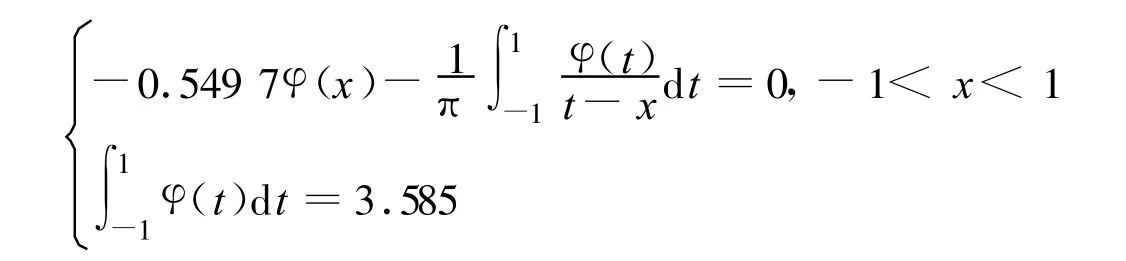
此题为第二类Cauchy奇异积分方程。因此,不能用Lobatto-Chbyshev求积公式法。

用Jacobi函数展开法。令N=4,得到

用Jacobi多项式展开法和分片连续函数法进行计算,所得数值结果见表2。

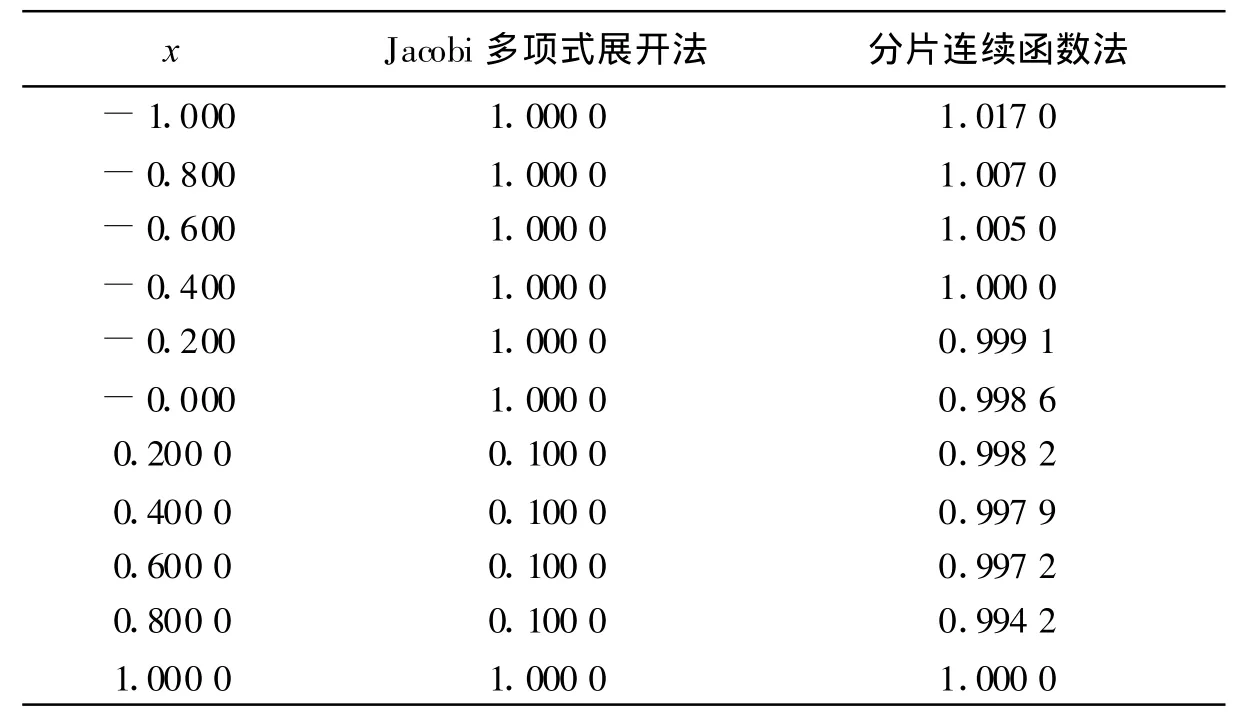
表2 两种数值解法g(x)结果比较

评价:这两种方法对于第二类Cauchy奇异积分方程都是适用的,尤其是Jacobi多项式展开法得到的结果是解析的,并不需要进行插值计算(-1,1)区间内其它的点的函数值,精确度很高;分片连续函数法是通过插值计算得到这些点的函数值,也很接近精确值。若需要计算其他点的函数值,只要以这些点为基点进行插值即可。

3 超奇异积分方程的数值求解

3.1 有限部积分的定义

考虑以下积分[15]

其中:φ(t)在 L上有导数,且 φ′(t)∈H。又设 x为L上的一个内点,则按照柯西主值积分的定义,以 x为中心,作充分小半径 ε的圆周,分别在 x的两边交L于x′,x″两点。

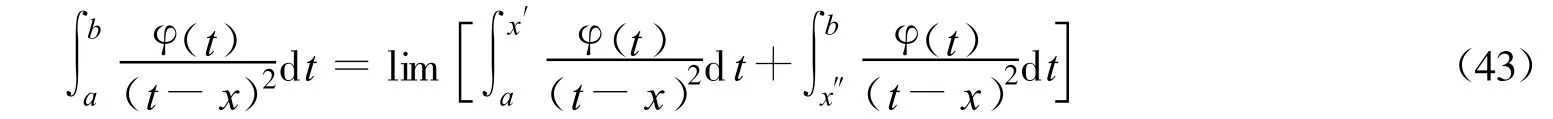
但是,这个积分一般不存在。我们可以利用分部积分法,得到

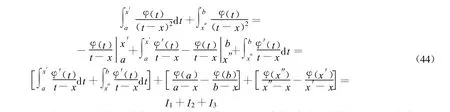
其中:I1是Cauchy奇异积分,它在主值意义下存在;I2是与ε无关的常数,它总是存在的;但I3是依赖于ε的,因而是发散,将结果引起积分发散的部分I3删去,定义

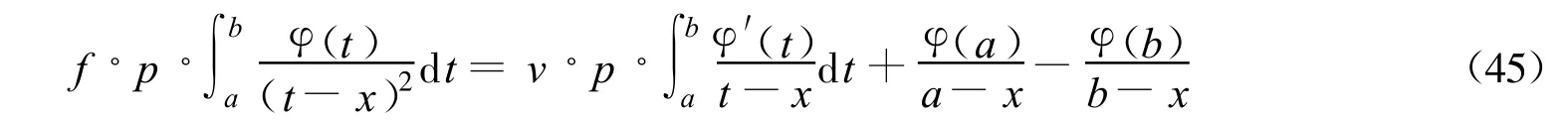
这就是超奇积分的“有限积分”定义,对于更高阶的超奇异积分,只要重复几次分部积分法,并且把引起积分发散的那些项删去,即可得到高阶奇异积分值,设L为一分段光滑弧段ab,n为一正整数,函数φ(t)∈Hn(即φ(n)(t)∈H)于L上,则高阶奇异积分的有限部积分定义为

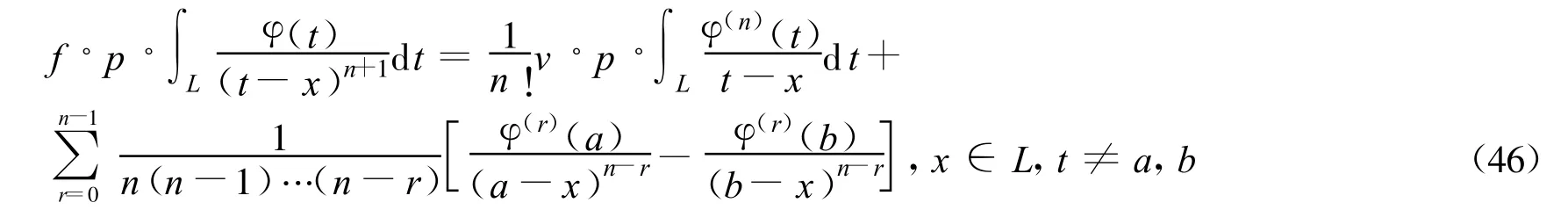
当L为封闭曲线时,上述积分公式右端只剩一项,即

以后遇见上面形式的积分时,恒理解为有限部积分,不再一声明。

3.2 多项式展开法

考虑如下形式的超奇异积分方程

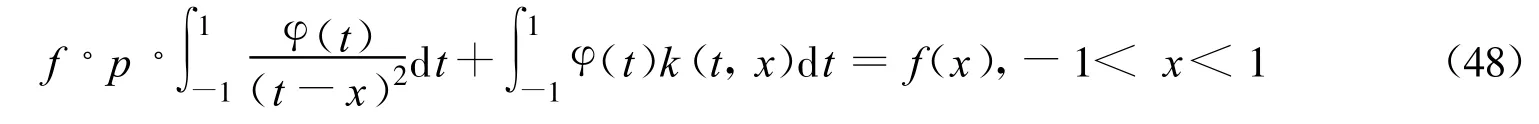
Erdogan[41]利用多项式展开法建立了超奇异积分方程的数值解法。多项式展开法是将未知函数写成连续函数与权函数之积的形式。根据不同的裂纹种类,连续函数可以展成第二类Chebyshev多项式截断级数和的形式,或者是幂级数和的形式。这种展开方式是为了更好地开展后续计算,如计算应力强度因子。

将方程的未知函数 φ(t)写成如下形式

其中:g(t)在[-1,1]上为有界连续函数;ω(t)是由问题的物理性质确定,对于裂纹问题,主要由裂纹尖端应力奇异性性质确定。

对于两端具有奇异性的内部裂纹:

对于只有一端具有奇异性的边缘裂纹:

其中有界连续函数g(t)可以近似表示为第二类Chebyshev多项式的截断级数

由有限积分结果得到[48]

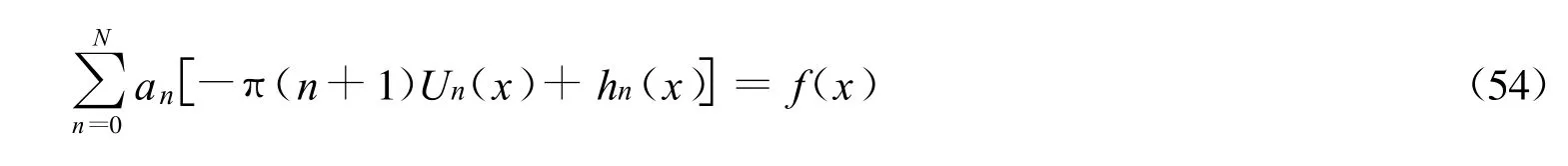
其中

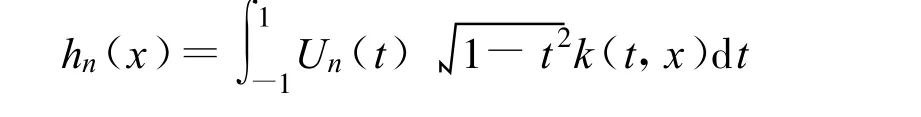
为了确定系数an,应适当选择配置点xi。一般xi关于原点对称分布,在区间端点处,分布密度应适当增加。因此,选择第二类Chebyshev多项式在(-1,1)上的N+1次的零点

则可以得到以下线性方程组

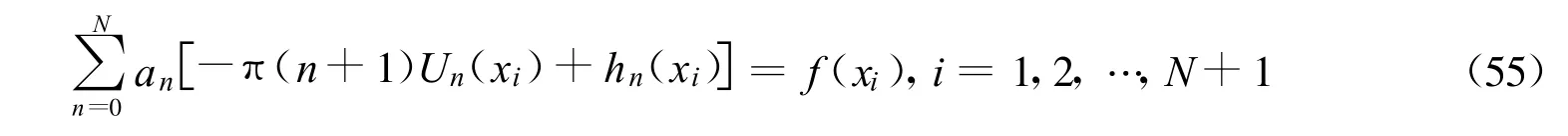
该线性方程组包含N+1个方程,N+1个未知数,因此方程组(55)有唯一解。在确定待定系数an后,将其代入(52)式和(53)式,则可以计算得到未知函数φ(t)。对于第一类奇异积分方程,线性代数方程组容易出现病态,可考虑让配置点的个数大于未知展开系数的个数,再利用最小二乘法进行求解。

②对于边缘裂纹,得到

由于g(t)在[-1,1]上为有界连续函数,因此可将其近似表示为幂级数的截断级数

由有限部积分结果[48]

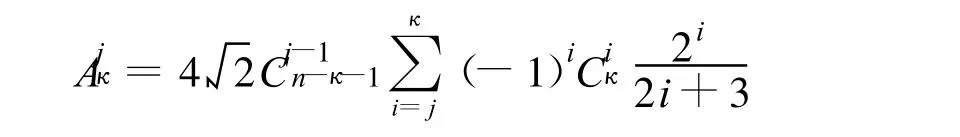
那么,方程可以推导为

其中

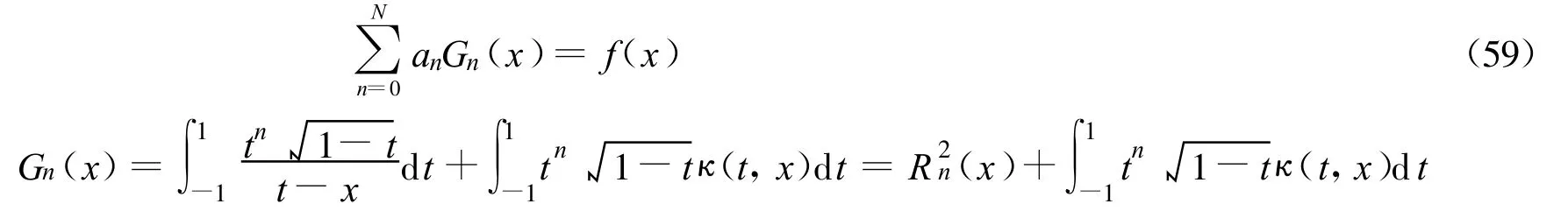
同样,为了确定系数an,可选择第二类Chebyshev多项式在[-1,1]上的N+1次零点

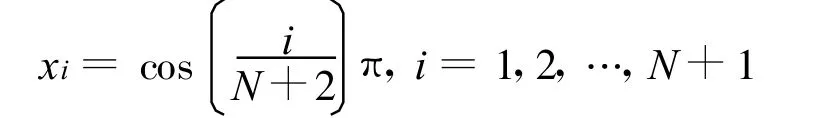
则可以得到以下线性方程组

该线性方程组包含N+1个方程,N+1个未知数,因此方程组(60)有唯一解。在确定待定系数后,将其代入(56)式和(57)式,则可以计算得到未知函数 φ(t)。

这种方法将超奇异积分方程转化为线性方程组,根据不同的裂纹形式,将g(t)展开成有限项级数和的形式。位置函数在断点的值需要进行插值计算,会有一定的误差,随着N的增加,精确度也会提高。

3.3 数值算例

算例3

该方程的解析解为 φ(x)=1,用多项式展开法求数值结果见表3,N分别取10,100,1 000。

表3 多项式展开法数值结果φ(t)(N值不同)

评价:超奇异积分方程的数值法的结果与解析解非常接近,在端点处需要插值计算,不能由公式直接得到,故误差比较大。当N值取得较大时,结果很接近解析解了。

4 结束语

对现有的一些奇异积分方程的数值解法进行了总结,重点是第一类和第二类的Cauchy奇异积分方程与超奇异积分方程的数值解法。这些方法主要思想是将奇异积分方程化成线性代数方程组,再进行求解。但是如果化成线性代数方程组,须采用不同的途径:有的利用特殊函数的正交性,将未知函数展开成特殊函数的级数形式,如Jacobi多项式展开法,Chebyshev多项式展开法;有的直接利用积分公式,将奇异积分直接用求和表示,如Gauss积分公式法,Lobatto-Chebyshev积分公式法;有的利用低阶插值函数去逼近未知函数,如分片连续函数法。途径不同,求解的误差和精度也不同,适用的范围也不同。一般应根据具体问题的特点,如未知函数在端点处的性质,方程等号右端的载荷项在积分区间的分布情况等,选择适宜的数值方法,此外,本文总结的几种超奇异积分方程的数值解法都涉及到方程基本解(权函数)的选取,权函数的形式一般由问题的物理性质确定。如对两端均有奇异性的内部裂纹,仅一端具有奇异性的边缘裂纹,他们对应的权函数是不相同的,一般应根据问题的性质具体问题分析。对于常系数奇异积分方程,权函数的形式也可以根据函数分析理论和奇异积分方程的指标理论由积分方程确定,就目前现状而言,对于常系数奇异积分方程的数值方法研究也还有待进一步深入。

[1]ERDOGAN F,GUPTA G D&COOK T S.Numerical solutions of singular integral equations,in:mechanics of fracture methodof analysis and solutions of crack problem[M].Leyden:International Publishing,1973:368-425.

[2]章梓茂.周期界面裂纹的弹性波散射问题研究[J].力学季刊,1994,15(1):14-26.

[3]汪越胜,王铎,马兴瑞,等.奇异积分方程在裂纹体弹性波散射问题中的应用[J].力学进展,1997,27:39-55.

[4]ANGEL Y C.On the reduction of elasto-dynamic crack Problems to singular integral equations[J].International of Journal Engineering Science,1988,26(7):757-764.

[5]IOAKIMIDIS N I.Application of finite-part integrals to the singular integral equations of crack problems in plane and three-dimensional elasticity[J].Acta Mechanica,1982,45(1):31-47.

[6]董春迎,谢志成,姚振汉,等.边界积分方程中超奇异积分的解法[J].力学进展,1995,25(3):424-429.

[7]汤任基,秦太验.三维断裂力学的超奇异积分方程方法[J].力学学报,1993,25(6):665-675.

[8]汤任基,秦太验.三维有限体中平片裂纹的超奇异积分方程方法——II数值方法[J].上海力学,1997,18(1):30-37.

[9]王爱勤,秦太验.三维有限体中两平行裂纹干扰问题的有限部分积分与边界元法[J].固体力学学报.1998,19(1):1-7.

[10]陈梦成,汤任基.三维裂纹问题的高精度数值解法[J].固体力学学报,2002,23(2):207-211.

[11]穆斯海里什维里.奇异积分方程[M].朱季纳,译.上海:上海科学技术出版社,1966.

[12]赵桢.奇异积分方程[M].北京:北京理工大学出版社,1984.

[13]候宗义,李明忠,张万国.奇异积分方程论及其应用[M].上海:上海科学技术出版社,1990.

[14]沈以淡.积分方程[M].北京:北京理工大学出版社,1992.

[15]路见可.解析函数边值问题[M].武汉:武汉大学出版社,2002.

[16]KARPENKO L N.Approximate solution of a singular integral equation by means of Jacobi Polynomials[J].Journal of Applied Mathematic Mechanism,1966,30(4):668-675.

[17]ERDOGAN F.Approximate solution of systems of singular integral equation[J].SIAM Journal of AppliedMathematics,1972,29(4):525-534.

[18]ERDOGAN F&GUPTA G D.On the numerical solution of singular integral equations[J].Quarterly of Applied Mathematics,1972,29(4):525-534.

[19]KRENK S.On quadrature formulas for singular integral equations of the first and second kind[J].Quarterly of Applied Mathematics,1975,32(3):225-232.

[20]KRENK S.On the use of interpolation polynomial for solutions of singular equations[J].Quarterly of Applied Mathematics,1975,32(3):479-484.

[21]IOAKIMIDIS N I&THEOCARIS P S.A comparison between the direct and classic numerical methods for solution of Cauchy-type singular integral[J].SIAM Journal Analysis,1980,17(1):115-118.

[22]THEOCARIS P S&IOAKIMIDIS N I.Numerical integral methods for solution of singular integral equations[J].Quarterly of Applied Mathematics,1977,35(2):173-183.

[23]GERASOULIS A&SRIVASTAV RP.A methodfor numerical solution of integral equationswith a principle vatue integral[J].International of Journal Engineering Science,1981,19(226):1 293-1 298.

[24]MILLER G R&KEER L M.A numerical technique for the solution of singular equations of the second kind[J].Quarterly of Applied Mathematics,1985,42(4):455-465.

[25]RUSSUL D K,THOMAS N F&SUN CT.The numerical solution of cauchy singular integral equations with applicationto fracture[J].International Journal of Fracture,1994,66(1):139-154.

[26]路见可,杜金元.奇异积分方程的数值解法[J].数学进展,1991,29(3):278-293.

[27]杜金元.奇异积分方程的一些求积公式[J].数学物理学报,1984,4(2):233-242.

[28]杜金元.奇异积分方程的数值解法(I)[J].数学物理学报,1985,5(2):205-223.

[29]杜金元.奇异积分方程的数值解法(II)[J].数学物理学报,1985,5(4):433-443.

[30]杜金元.高阶奇异积分的求积公式[J].数学年刊,1985,6A(5):625-636.

[31]杜金元.高阶奇异积分的求积公式(II)[J].数学杂志,1986,6(4):439-454.

[32]杜金元.带Hilbert核的奇异积分方程的数值解法[J].计算数学,1989,2(2):248-266.

[33]王小林.一类奇异积分方程组的样条间接近似解法[J].数学杂志,1996,17(1):113-116.

[34]王小林.封闭曲线上奇异积分方程的样条逼近解法[J].数学物理学报,1997,17(3):348-355.

[35]魏培君,章梓茂.求解Cauchy型奇异积分方程的数值解法[J].数值计算与计算机应用,2003,24(1):36-43.

[36]ROOKE D P,SNEDDON I N.The crack energy and stress intensity factor for a cruciform crack deformed by internal pressure[J].International Journal of Engineering Science,1969,7(6):1 079-1 089.

[37]QU JIANMIN.Internal crack Loaded by a time-harmonic plane wave[J].International Journal of Solids Structures,1994,31(3):329-345.

[38]张建勇,李星.各向异性平面含斜裂纹的奇异积分方程方法[J].力学季刊,2004,25(2):248-255.

[39]HADMARD J.Lectures on Cauchy Problem in Linear Partial Differential Equations[M].USA:Yale Universtiy Press,1923.

[40]KUTT H R.The numerical evaluation of principal value integrals by finite-part integration[J].NumericalMathematics,1975,24(2):205-210.

[41]KAYA A C&ERDOGAN F.On the solutionof integral equationswith strongly singular kernel[J].Quarterly of Applied Mathematics,1987,45(1):105-122.

[42]汤任基.断裂力学中的两类奇异积分方程[J].上海交通大学学报,1990,24(5):36-46.

[43]CHAN YOUNSHA,FANNJIANG A C&PAULINO G H.Integral equationswith hypersingular kernels theory and applications to fracture mechanics[J].International Journal of Engineering Science,2003,42(4):683-720.

[44]乐金朝,汤任基.双材料中平片裂纹问题的超奇异积分方程解法[J].应用力学学报,1999,16(4):1-6.

[45]杜云海,徐建国,温玲君,等.双材料平行于界面裂纹问题的超奇异积分方程法[J].机械强度,2003,25(2):174-177.

[46]杜云海,乐金朝.双材料平面裂纹问题的超奇异积分方程解法[J].机械强度,2004,26(3):236-331.

[47]乐金朝,杜云海.双材料平面多裂纹问题的超奇异积分方程解法[J].岩石力学与工程学报,2004,23(22):3 834-3 839.

[48]陈梦成.三维断裂力学问题求解—超奇异积分方程方法[M].成都:西南交通大学出版社,2007

[49]CHENMENGCHENG,NODA NAOAKI&TANG RENJI.Application of finite-part integral to planar interfacialfracture problemsin3D bimaterials[J].ASME Journal of Applied Mechanics,1999,66(4):885-890.

[50]CHEN MENGCHENG.Application of finite-part integrals to three-dimensional fracture problems for piezoelectric media,Part II:Numerical analysis[J].International Journal of Fracture,2003,121(1):149-161.

[51]陈梦成,张安哥.横观各向同性的三维断裂力学问题[J].力学学报,2006,38:612-617

[52]陈梦成,张安哥,野田尚昭.压电材料中三维 I型断裂力学分析[J].力学学报,2005,37(1):15-23

[53]CHEN MENGCHENG.Application of finite-part integrals to three-dimensional fracture problems for piezoelectric media,Part I:hypersingular integral equation and theoretical analysis[J].International Journal of Fracture,2003,121(1):133-148

[54]ZHU BOJING,QIN TAIYAN.3D modeling of crack growth in electro-magneto-thermo-elastic coupled viscoplastic multiphase composites[J].Applied Mathematical Modelling,2009,33(2):1 014-1 041

[55]XU C H,QIN T Y,NODA N A.Numerical solutions of singular integral equationsfor planar rectangular interfacial crack in 3D biomaterial[J].Applied Mathematics and Mechanics,2007,28(6):751-757

[56]朱伯靖,秦太验.磁电热弹耦合材料三维多裂纹问题的超奇异积分法[J].力学学报,2008,40(1):46-58.