脉冲噪声环境下循环ESPRIT新方法

兰天，邱天爽，杨娇

（大连理工大学 电子与信息工程学院，辽宁 大连 116024）

1 引言

现代移动通信和集成传输系统的迅速发展，使电磁波的传输环境变得越来越复杂，并且对高分辨波达方向估计和减少干扰波影响的技术要求也越来越高[1]。在这些技术中，cyclic-MUSIC[2]（循环MUSIC）和 cyclic-ESPRIT[2]（循环 ESPRIT）2类算法可以利用到达波的循环平稳性[3,4]有选择性地估计波达方向，且估计精度也很高，因而受到广泛重视。与cyclic-MUSIC算法相比较，cyclic- ESPRIT算法无需谱峰搜索因而运算量少,且具有稳健性等优点，更适合在工程上的应用。在cyclic- ESPRIT类算法中，TLS-cyclic-ESPRIT（总体最小二乘循环ESPRIT）算法性能更好，因为此算法可以把一个较大维数病态广义特征问题转化为一个较小维数的无病态广义特征问题[5]。

但是当实际环境中存在脉冲噪声时，cyclic-ESPRIT类算法的性能会明显退化甚至失效，这是因为脉冲噪声可能不存在有限的二阶统计量[6]。文献[7,8]表明，现实环境中的确存在着大量脉冲噪声，例如环境噪声、雷达杂波以及水下声波信号、人造信号等，这些脉冲性噪声难以用高斯模型描述，而往往采用具有厚拖尾的α稳定分布[7]过程来描述。根据脉冲性噪声的特性和 cyclic-ESPRIT算法存在的问题，本文提出了分数低阶循环相关矩阵的概念，并在此基础上，提出了分数低阶总体最小二乘（TLS）循环ESPRIT算法的2种新形式。新算法保留了 cyclic-ESPRIT类算法的优良性能，并对脉冲噪声有较强的抑制作用，其性能显著优于传统的cyclic-ESPRIT算法。

2 信号噪声模型

如图1所示，设阵元数为M的天线阵列为线性均匀阵列[9]，各相邻阵元间的距离为 d ≤λ0/2，其中 ， λ0=2πc/ω0,ω0为 信 号 的 中 心 频 率 。为l个入射信号，假定s1( n), s2( n),… ,sKa(n)为指定的循环频率的循环平稳信号，且为非相干源。其他 l - Ka个信号为非指定循环频率的信号；入射角分别为 θ1, θ2,… ,θl。第i个信号到达各个阵元的相位差所组成的向量为：第k个阵元上的接收信号为

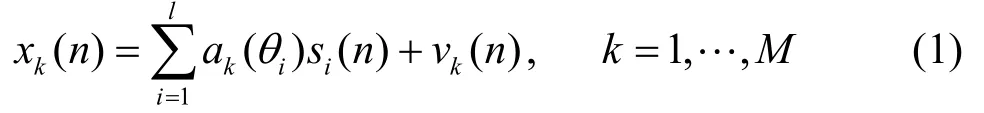
图1 阵列模型

2.1 ESPRIT算法形式1的信号噪声模型

x (n)=A1S (n)+ v( n)，y (n )=A1ΦS (n)+v (n+1)其中， A1为此算法的天线阵列的方向矩阵，将其写成Vandermonde矩阵形式，有：为天线阵列接收到的噪声矢量，假定各个阵元接收噪声均服从α稳定分布，且与信号循环互不相关。

2.2 ESPRIT算法形式2的信号噪声模型

把M个阵元组成线阵分为2个子阵，其中子阵列1由第1个至第 1M- 个阵列组成，子阵2由第2个至第M个阵元组成。由式（1）得整个阵列输出为

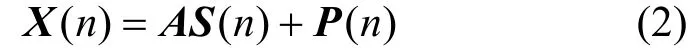
则：

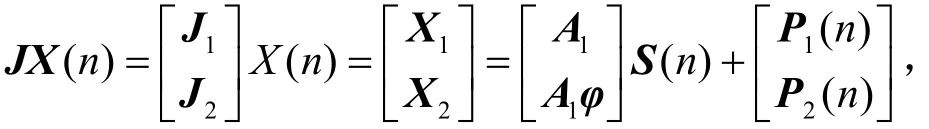
其中，A =[a(θ1) , a(θ2), … ,a(θl)]为天线阵列的方向矩阵，φ是一酉矩阵，所以 X1和 X2具有相同的信号子空间和噪声子空间。 Ρ(n)= [v1(n), v2( n ) ,… ,vM(n) ]为天线阵列接收到的噪声矢量，假定各个阵元接收噪声均服从α稳定分布，且与信号循环互不相关。

2.3 α稳定分布的概念

α稳定分布是唯一一类满足广义中心极限定理的分布[6,7]。与高斯分布相比，α稳定分布具有更厚的统计拖尾，因此其时域实现具有显著的脉冲特性。α稳定分布并没有闭合的表达式，但可以用它的特征函数来方便地表示α稳定分布。

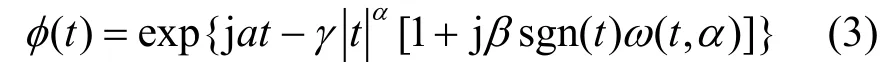
式中，

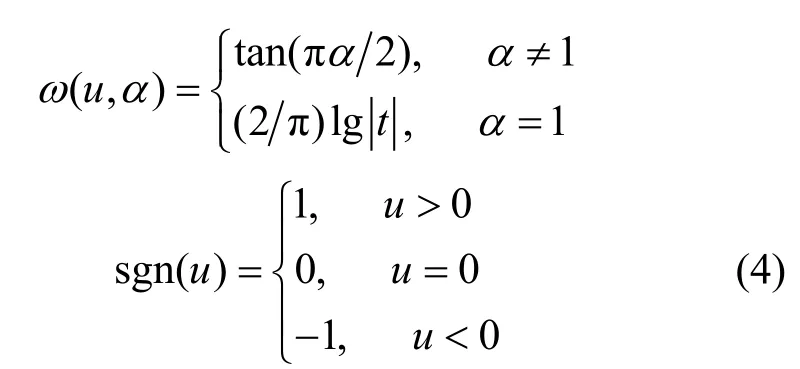
其中， - ∞＜a＜∞,γ＞ 0,0 ＜α≤2,-1 ≤ β≤1。

由上式可见，α稳定分布的特征函数由α、β、γ、a 4个参数即可确定。α为特征指数，它决定该分布脉冲特性的程度。α越小，所对应的分布拖尾越厚，脉冲特性越显著。β为对称参数，0β=对应于对称分布，简称SαS分布。γ为分散系数，类似于高斯分布中的方差。a称为位置参数，对于SαS分布，a表示中值或均值。当2α=时，其特征函数与均值为a，方差为22σ的高斯分布相同，即高斯分布是α稳定分布的一个特例。定义02α＜＜的非高斯稳定分布为分数低阶α稳定分布。

3 分数低阶循环ESPRIT算法

经典的循环ESPRIT类算法通常是把加性噪声假设为高斯噪声，利用阵列输出信号的二阶循环统计量进行波达方向（DOA) 估计。但是如果信号模型与实际的信号环境不匹配，则会使算法的估计性能下降，甚至失效。即当信号被高斯噪声污染时，基于二阶循环统计量的算法可以很好地抑制相关噪声和干扰，提取有用信号的信息。但是，当信道中存在没有二阶统计量的 alpha稳定分布的脉冲噪声时，经典的循环ESPRIT类算法是不能有效滤除或抑制这种噪声的。因此，本文提出了分数低阶循环ESPRIT算法。

3.1 分数低阶循环相关矩阵

针对分数低阶α稳定分布条件下，二阶统计量的循环ESPRIT算法存在退化问题，本文提出了一种新的估计矩阵——分数低阶循环相关矩阵为

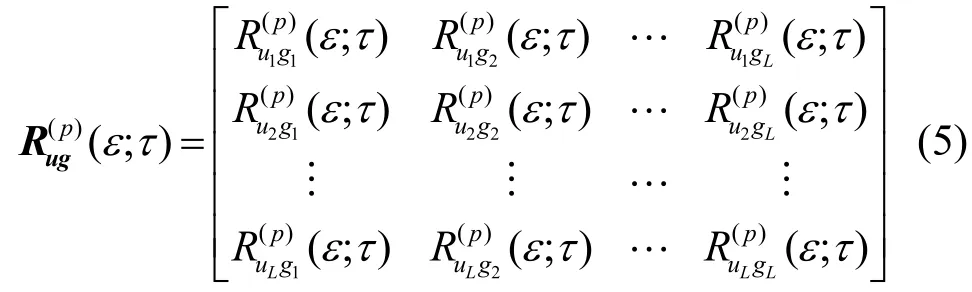
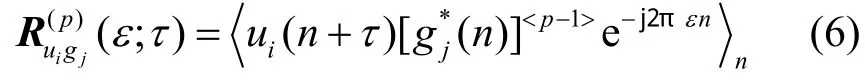
本文提出的分数低阶循环ESPRIT算法，分为2种形式：分数低阶总体最小二乘循环ESPRIT算法形式 1和算法形式 2(分别简称为 FLOM-TLS-cyclic-ESPRIT1 和 FLOM-TLS-cyclic-ESPRIT2)。

3.2 FLOM-TLS-cyclic-ESPRIT1

根据 x(n)和 y (n)的定义，由式（5）得出(M-1)×( M- 1)维分数低阶循环相关矩阵为由式（6）得到的第i行、第j列元素为

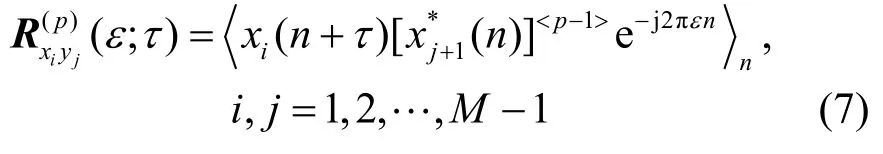
把式(1)代入式(7)得

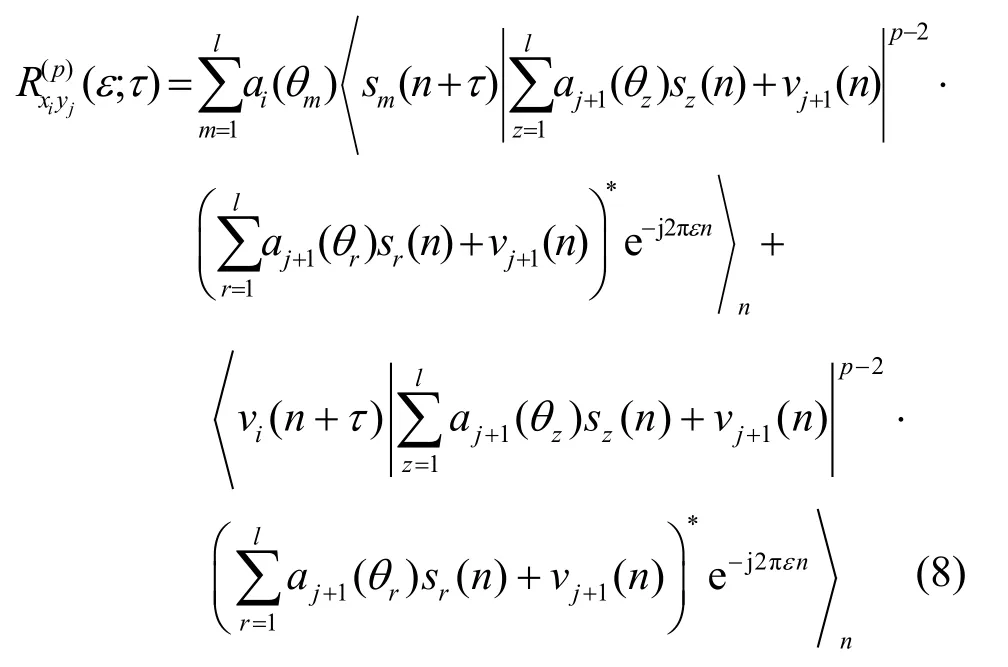
[10]的证明，可写成

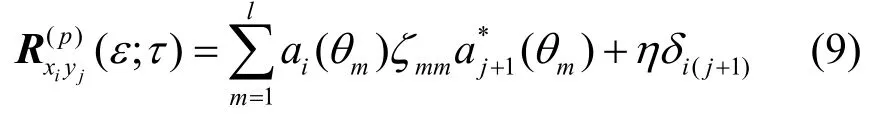
其中：当 m = 1和 m ＞Ka时，ζm(j+1)= 0 ;当1 ＜m≤ Ka时，

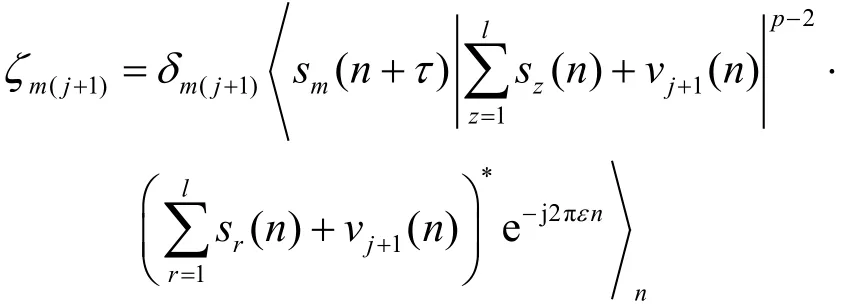
其中，(1)mjδ+为克罗内克尔符号。因为只有aK个信号为指定循环频率的循环平稳信号，其他非指定循环频率的信号都为零。由于噪声不存在非零的循环频率，因此η为零。

其中，Λ1的第i行、第j列元素为ζij，i, j = 1,2,…,l 。同理可求得

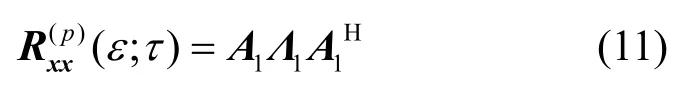
可以看出式（10）和式（11）与二阶循环相关矩阵[2]表达式类似，之后按照循环 ESPRIT的方法估计波达方向。，因为矩阵A1满列秩， Λ1非奇异[1]，所以矩阵和I - λΦH的广义特征值完全相等。其中，λ为的广义特征值。为了使做广义特征值的矩阵束的维数减小，提高估计精度，本文使用TLS方法，对做截尾奇异值分解，得到。求矩阵束的广义特征值分解，得到单位圆上的个广义特征值，由确定波达方向。

3.3 FLOM-TLS-Cyclic-ESPRIT2

根据 x ( n)和 y ( n)的定义，由式（5）得出(M - 1 )×(M - 1 )维分数低阶循环相关矩阵为由式（6）得到的第i行、第j列元素为

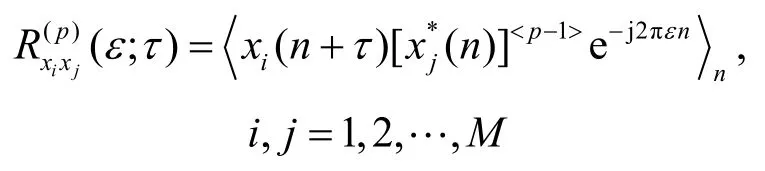
与3.2节中推理步骤相同，可以得到

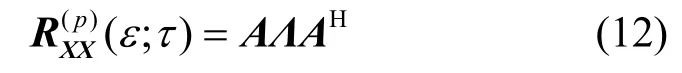
其中，Λ的第i行、第 j列为：

①当1 ≤ i≤ Ka时，

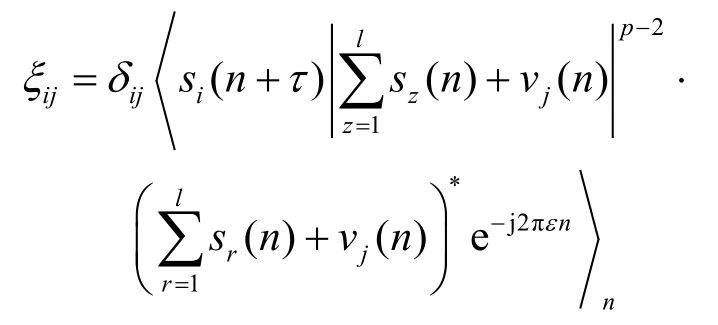
②当Ka＜i≤l时，ξij=0，i, j = 1 ,2,… ,l 。

4 仿真实验结果

本文采用广义信噪比（GSNR, generalized signal-noise-ratio）为 1 0lg(γ)来描述SαS过程的信噪比[7]。其中 γ ( γ ＞ 0 )表示SαS噪声的分散系数，表示信号功率。实验采用8阵元均匀线阵，阵元距为半个波长。入射源为2个BPSK信号，其中，目标信号的入射角为30°，载频为100MHz；干扰信号为入射角为60°，载频为30MHz。这里的均方根误差定义为辐射源的波达方向估计的样本均方根误差。即， ˆ()n为第n次实验的估计值，N为实验总次数。

实验1 G SNR= 1 5dB ,循环频率取200MHz，p从0.5取到2，每个p值仿真200次，取均方根误差。

由图2(a)可以得出，当 p = 1 .3时，此算法DOA估计误差最小。由图2(b)可以得出，当 p = 1 .4时，此算法DOA估计误差最小。当 p = 2 时，FLOM-TLS-cyclic-ESPRIT类算法退化为TLS-cyclic-ESPRIT类算法，估计误差较大。在使用本文提出的新算法时，首先找到在给出的脉冲环境中最优的p值，之后再按照这个p值进行新算法的角度估计。

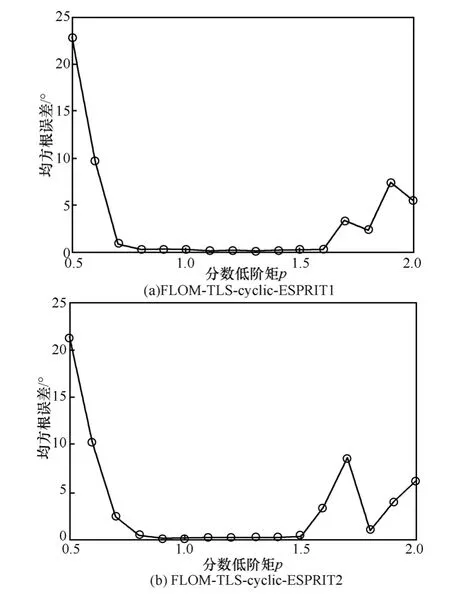
图2 p取不同值时，对FLOM-TLS-cyclic-ESPRIT类算法的影响

实验2 G SNR=15dB、α=1.5的SαS噪声环境下 FLOM-TLS-cyclic-ESPRIT类算法与 TLS-cyclic-ESPRIT算法的比较。参照实验1，FLOM-TLS-cyclic-ESPRIT1算法的p取1.3, FLOM-TLS-cyclic-ESPRIT2算法的p取1.4。仿真分别独立进行了2 000次。

从表1和表2中可以得到，FLOM-TLS-cyclic-ESPRIT类算法的性能明显好于 TLS-cyclic-ESRPIT类算法。在α稳定分布噪声的条件下，TLS-cyclic-ESRPIT算法的稳定性差，估计精度低。而FLOM-TLS-cyclic-ESPRIT类算法稳定性很好，估计精度高，可以很好地抑制了α稳定分布噪声，比较准确地估计出了源信号的 DOA。同时可以得到在这个广义信噪比条件下，FLOM-TLS-cyclic- ESPRIT1算法的性能优于FLOM-TLS-cyclic- ESPRIT2。

表1 TLS-cyclic-ESPRIT算法形式1和FLOM-TLS-cyclic-ESPRIT1算法结果比较

表2 TLS-cyclic-ESPRIT 算法形式2 和FLOM-TLS-cyclic-ESPRIT2 算法结果比较

实验3 广义信噪比从 15dB- 到15dB增大时，均方根误差的变化，其他条件同上。每个广义信噪比的取值都独立仿真200次。

图3 FLOM-TLS-cyclic-ESPRIT类算法的抗噪性能分析

从图 3(a)中可以看出，FLOM-TLS-cyclic- ESPRIT1算法和TLS-cyclic-ESPRIT算法形式1在广义信噪比比较低（ 15dB- ～5dB- ）时，抗噪性能基本相当；当广义信噪比升高时，FLOM-TLS-cyclic-ESPRIT1算法抗噪性能明显好于TLS-cyclic- ESPRIT算法形式1。从图3(b)中可以看出，FLOM-TLS-cyclic-ESPRIT1算法的抗噪性能明显好于 TLS-cyclic- ESPRIT算法形式2。从图3(c)中可以看出，FLOM-TLS-cyclic-ESPRIT1算法和FLOM-TLS-cyclic-ESPRIT2在广义信噪比比较低（ -1 5dB～ -5 dB）时，FLOM-TLS-cyclic-ESPRIT2的抗噪性能较好；当广义信噪比升高时，FLOM-TLS-cyclic-ESPRIT1算法抗噪性能稍微好于 FLOM-TLS-cyclic-ESPRIT2。FLOM-TLS-cyclic-ESPRIT1算法在低广义信噪比时性能下降的原因应该是p值的选择，在不同的广义信噪比下，最优的p值是不同的。

实验 4 为验证本文算法的广泛适用性，对入射源为QPSK信号的情况进行仿真实验。入射源为2个QPSK信号，其中，目标信号入射角为30°，载频为100MHz，键控速率为50MHz；干拢信号入射角为60°，载频为30MHz，键控速率为3MHz。在 G SNR=15dB 、α=1.5的SαS噪声环境下，循环频率取为 2倍键控速率100MHz。p从0.5取到2（间隔为0.1），每个p值仿真200次，取均方根误差最小时对应p值对 FLOM-TLS-cyclic-ESPRIT1算法与 FLOM-TLS-cyclic-ESPRIT2算法进行仿真比较。仿真分别独立进行了2 000次。

通过对表1～表3的对比看出，本文提出算法对QPSK信号的DOA效果较好，但对BPSK信号具有更高的估计精度。可以表明本文的FLOM-TLS-cyclic-ESPRIT1算法和 FLOM-TLS-cyclic-ESPRIT2算法具有较为普遍的适用性。

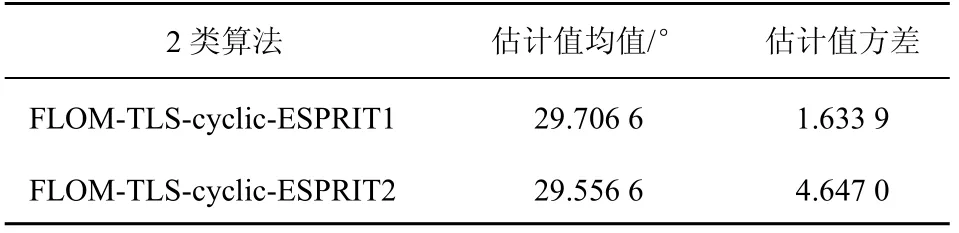
表3 FLOM-TLS-cyclic-ESPRIT1与FLOM-TLS-cyclic-ESPRIT2算法结果比较

5 结束语

循环统计量是一种研究具有循环平稳特性的非平稳随机信号的有效工具，但是广泛存在的脉冲性非高斯分布噪声会降低基于传统二阶循环统计量的各类算法的性能。本文以α稳定分布作为噪声模型，考虑了非高斯噪声对传统的二阶循环统计量的影响，给出了分数低阶循环相关矩阵的概念，同时结合高分辨波达方向估计技术，提出基于分数低阶循环相关矩阵的ESPRIT新方法，仿真表明该方法可以有效消除α稳定分布噪声及相关干扰对角度估值的影响，具有潜在的应用前景。

参考文献：

[1] INAGAKI Y, KIKUMA N. DOA estimation of desired signals by cyclic ESPRIT based on noise subspace and its performance improvement[J].Electronic and Communications in Japan , 2007, 90 (11)∶ 95-104.

[2] GARDNER W A .Simplification of MUSIC and ESPRIT by exploitation of cyclostationarity[J]. Proceedings of the IEEE, 1988, 76 (7)∶ 845-847.

[3] 王宏禹.非平稳随机信号分析与处理[M].北京：国防工业出版社,1999.WANG H Y. Nanstationary Random Signal Analysis and Processing[M]. Beijing∶National Defence Industry Press,1999.

[4] GARDNER W A, NAPOLITANO A, PAURA L. Cyclostationarity∶half a century of research[J]. Elsevier Science Signal Processing, 2006,86(44)∶ 639-697.

[5] 张贤达.现代信号处理（第二版）[M].北京：清华大学出版社,2002.ZHANG X D. Modern Signal Processing Second Edition[M].Beijing∶Tsinghua University Press,2002.

[6] SHAO M, NIKIAS C L. Signal processing with fractional lower order moments∶ stable processes and their applications[J]. Proceedings of the IEEE, 1993, 81(7)∶986-1010.

[7] NIKIAS C L, SHAO M. Signal Processing with Alpha Stable Distributions and Applications[M]. New York∶ John Wiley & Sons Inc，1995.

[8] TSIHRINTZIS G A, NIKIAS C L. Fast estimation of the parameters of alpha-stable impulsive interference[J].IEEE Transactions on Signal Processing,1996,44 (6)∶1492-1503.

[9] 王永良,陈辉，彭应宁等. 空间谱估计理论与算法[M].北京：清华大学出版社,2004.WANG Y L,CHEN H,PENG Y N, et al. Spatial Spectrum Estimation[M]. Beijing∶ Tsinghua University Press,2004.

[10] LIU T H, MENDEL J M. A subspace-based direction finding algorithm using fractional lower order statistics[J]. IEEE Transactions on Signal Processing, 2001, 49( 8)∶ 1605-1613.