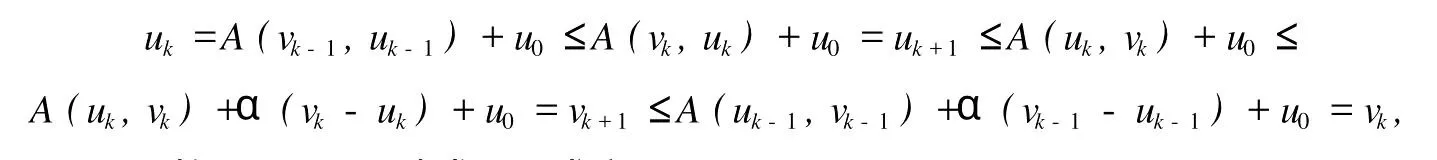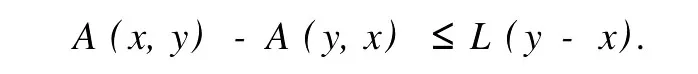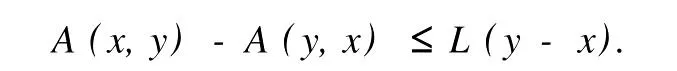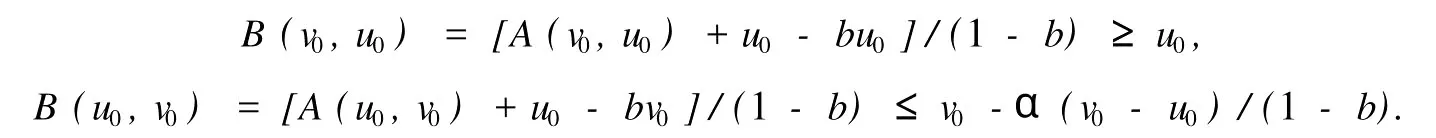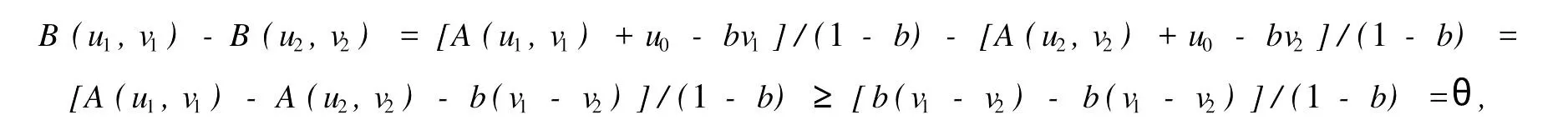一类不具有连续性和紧性条件的反向混合单调算子方程解的存在性定理＊

李庆芳

(河南化工职业学院公共课教学部,河南郑州450042)

一类不具有连续性和紧性条件的反向混合单调算子方程解的存在性定理＊

李庆芳

(河南化工职业学院公共课教学部,河南郑州450042)

在半序空间中,研究了不具有连续性和紧性条件的一类反向混合单调算子方程解的存在与惟一性,并给出迭代序列收敛于解的误差估计,所得结果是某些已有结果的本质改进和推广.

正规锥;反向混合单调算子;算子方程;方程解

混合单调算子和反向混合单调算子是两类重要的算子,关于Banach空间中非线性混合单调算子方程A(x,x)=x的迭代求解问题,已有许多研究[1～7],并得到了一批好的结果,但对于反向混合单调算子方程A(x,x)+u0=x解的存在性问题却涉及甚少.本文利用了非对称迭代法解决了半序空间中惯用的对称迭代法所无能为力的问题,讨论了反向混合单调算子方程A(x,x)+u0=x解的存在惟一性,并给出了迭代序列收敛于解的误差估计,改进和推广了已有文献中的相应结果.

1 预备知识

本文总假设E为具有正规锥P的半序实Banach空间,θ表示E中的零元素,N为P的正规常数,关于锥和半序理论参见文献[8].设u0,v0∈E且u0

定义1[1]称二元算子A:D×D→E为混合单调算子,如果A(x,y)对每一个固定的y∈D关于x是增的,对每一个固定的x∈D关于y是减的.

定义2[8,9]称二元算子B:D×D→E为反向混合单调算子,若:

1)对每个固定的v∈D,B(u,v)在D上关于u是单调递减的,即∀u1

2)对每个固定的u∈D,B(u,v)在D上关于v是单调递增的,即∀v1

2 主要结果

定理1 设P是实Banach空间E中正规锥,A:D×D→E是反向混合单调算子,且满足: 1)存在

2)存在正有界线性算子L:E×E→E且其谱半径r(L)<1,使得对任意的x,y∈D,x≤y有

则当0<α+r(L)<1时,方程A(x,x)+u0=x在[u0,v0]中有惟一解且对迭代序列

有误差估计式中γ=α+r(L).

证明 运用归纳法易证

事实上,当n=1时,由式(1)、(2)及A是反向混合单调算子,我们有

v1-u1=A(u0,v0)-A(v0,u0)+α(v0-u0)≥θ,即u0≤u1≤v1≤v0,式(5)成立.

假设n=k时,式(5)也成立,即uk-1≤uk≤vk≤vk-1,则当n=k+1时,有

即 uk≤uk+1≤vk+1≤vk,故n=k+1时式(5)成立.

由式(2)、(3)和(5)可得

式中H=αI+L,I是恒等算子,对任给的0

存在n0,使得‖Hn‖<γn,n≥n0,考虑到P的正规性知

故由式(6)知,对任意正数n,p有θ≤un+p-un,vn-vn+p≤vn-un≤Hn(v0-u0),

从而由式(7)与P的正规性知

所以{un}是Cauchy序列,由E的完备性及{un}∈[u0,v0],存在

同理可证{vn}也是Cauchy序列.于是存在

又由式(3)、(8)及A是反向混合单调算子有

可得

故有

即x＊是方程A(x,x)+u0=x在[u0,v0]中的解.

再证不动点的惟一性:设y＊也是A在[u0,v0]中的不动点,则仿上述证明由归纳法易得令 n→∞得是方程A(x,x)+u0=x在[u0,v0]中的惟一解.

误差估计式(4)由式(7)易得.

定理2 设P是实Banach空间E中正规锥,A:D×D→E是反向混合单调算子,且满足:

1)存在α∈[0,1],(1-α)(u0-v0)≤A(v0,u0),A(u0,v0)≤θ;

2)存在正有界线性算子L:E×E→E且其谱半径r(L)<1,使得对任意的x,y∈D,x≤y,有

则当0<α+r(L)<1时,方程A(x,x)+v0=x在[u0,v0]中有惟一解有误差估计

证明 类似于定理1的证明,略.

定理3 设P是实Banach空间E中正规锥,A:D×D→E是反向混合单调算子,且满足:

1)存在α∈[0,1],∈[0,1],有

2)存在正有界线性算子L:E×E→E且其谱半径r(L)<1,使得对任意的x,y∈D,x≤y有

则当0<α+β+r(L)<1时,方程A(x,x)=x在[u0,v0]中有惟一解且对迭代序列有误差估计其中γ=α+β+r(L).

下面讨论A未必反向混合单调时的一些结论.

定理4 设P是实Banach空间E中正规锥,A:D×D→E是二元算子,且满足:

1)若存在α∈[0,1],满足初始条件θ≤A(v0,u0),A(u0,v0)≤(1-α)(v0-u0);

2)存在b>0,使得b(y1-y2)≤A(x1,y1)-A(x2,y2),u0≤x1≤x2≤v0,u0≤y2≤y1≤v0;

3)存在正有界线性算子L:E×E→E且其谱半径r(L)<1,使得对任意的x,y∈D,x≤y有

则当0<[α+r(L)-b]/(1-b)<1时,方程A(x,x)

证明 令B(x,y)=[A(x,y)+u0-by]/(1-b),x,y∈D.由1)知,

又由2)知,对任给的ui,vi∈D,(i=1,2),当u2≥u1,v2≤v1时,

所以B(u1,v1)≥B(u2,v2),即B:D×D→E是反向混合单调算子.

再由3)知,

构造迭代序列un+1=B(vn,un),vn+1=B(un,vn)+α(vn-un)/(1-b),则仿文献[6]中定理的证明可得B(x,x)=x在D中有惟一解(1-b)的惟一解.仿上证明可得下面结论.

定理5 设P是实Banach空间E中正规锥,A:D×D→E是二元算子,且满足:

1)存在α∈[0,1],满足初始条件(1-α)(u0-v0)≤A(v0,u0),A(u0,v0)≤θ;

2)存在b>0,使得b(y1-y2)≤A(x1,y1)-A(x2,y2),u0≤x1≤x2≤v0,u0≤y2≤y1≤v0;

3)存在正有界线性算子L:E×E→E且其谱半径r(L)<1,使得对任意的x,y∈D,x≤y有

则当0<[α+r(L)-b]/(1-b)<1时,方程A(x,x)+v0=x在[u0,v0]中有惟一解x＊.

注1 本文定理4,5中研究了算子A未必反向混合单调时仍有相应的结论,拓宽了定理的适用范围.

注2 本文结论对算子A在连续性和紧性方面没有作任何假定.

[1]Guo Dajun,Lakshmikantham V.Coupled fixed points of nonlinear operators with applications[J].Nonlinear Anal T MA,1987,11 (5):623-632.

[2]颜心力.对称压缩算子方程解的存在惟一性定理及其应用[J].科学通报,1990,35(10):733-736.

[3]张庆政.序对称压缩算子方程的迭代求解及其应用[J].工程数学学报,2000,17(2):131-134.

[4]徐裕生,孙俊萍.一类混合单调算子方程解的存在惟一性定理[J].陕西师大学报,2002,30(3):1-4.

[5]孙义静.一类非线性算子方程组的迭代算法及应用[J].浙江大学学报,1999,33(3):289-294.

[6]李俊强,张斐然.一类混合单调算子的新不动点定理的推广[J].郑州大学学报,2004,36(4):13-15.

[7]TaylorA E,LayD C.Introduction to FunctionalAnalysis[M].New York:spinger-verlag,1980;277-281.

[8]郭大钧.非线性泛函分析[M].济南:山东科技出版社,1985.

[9]栾世霞,孙钦福,赵艳玲.反向混合单调算子新的不动点定理[J].吉首大学学报,2008,29(1):7-9.

Existence Theorem of Solution of Anti-m ixedMonotone Operator Equation without the Conditions of Cont inuity and Compactness

LIQing-fang

(Dept.of Public Courses,Henan Vocational College of Chemical Technology,Zhengzhou Henan 450042,China)

The paper discusses the existence and uniqueness of solution of anti-mixed monotone operator equation in semi-ordered space without the conditions of continuity and compactness,and the error estimations that iterative sequences converge to solutions are given.The results presented here improve and generalize some correspondingresults for anti-mixed monotone operators.

normal cone;anti-mixed monotone operator;operator equation;equation solution

book=9,ebook=375

O 177.91

A

1673-2103(2010)05-0032-04

2010-06-11

河南省教委科研基金资助项目(200810483004)

李庆芳(1973-),女,河南郑州人,讲师,研究方向:非线性泛函分析及其应用.