论二次分式函数的值域
●
(杭州市第九中学 浙江杭州 310020)
论二次分式函数的值域
●龚雷陈伟
(杭州市第九中学 浙江杭州 310020)

对于二次分式函数的值域问题,比较流行的解法是判别式法,但此法并不可靠.这一点已有不少文献指出,但这些文献基本上只是面向中学生的解题易错点作出提醒,未从解法的理论依据进行研究.本文拟对此作个补遗,同时给出二次分式函数值域问题的另一种新的解决思路.
1 判别式法的理论依据
判别式法实质上就是运用函数与方程的思想以及化归思想,把函数值域问题化归为二次方程的根的讨论问题.为了看清判别式法的理论依据,我们把这一化归过程细化为以下问题链:


(3)若关于x的方程
(a2y-a1)x2+(b2y-b1)x+(c2y-c1)=0
(1)
至少有1个实根,求y的取值范围.
问题(1)是原问题,将问题(1)化归为问题(2)的理论依据是函数的概念,这一过程不存在什么问题,这是一个等价转换;从问题(2)转化到问题(3)是一个方程同解变形过程,根据方程同解理论可知,这里去分母有可能产生增根,因此这在理论上讲是一个不等价转换,很多人以为判别式法的问题主要源自于这个不等价转换.但追问一下“何时产生增根”就不难发现,当且仅当分子分母可约时有增根.而此时这个函数可以化简为一次分式函数甚至常函数.因此对于分子分母不可约的一般情况而言,这个不等价转换并不会影响结论.

2 判别式法的局限性
从以上讨论可以看出,只要在问题(3)中不忘讨论方程(1)的二次项系数是否为0,用判别式法求二次分式函数的值域并不存在太大的问题.
事实上,判别式法的局限性主要在还于当函数定义域不是自然定义域时,问题(2)、(3)中的“至少有1个实根”相应改成“在规定的定义域内至少有1个实根”,此时问题化归为二次方程根的分布问题,要分“2个根均在定义域内(包括重根)”和“1个根在定义域内1个根在定义域外”这2种情况讨论,再加上二次项系数是否为0的讨论,共需讨论3种情况.如例1所示:

解原问题等价于:关于x的方程

在区间[0,1]上至少有1个实根,求y的取值范围.
(1)当y=1时,x=-2∉[0,1];
(2)当y≠1时,Δ=-3y2-4y+8.记
f(x)=(y-1)x2+(y-2)x+(y+1),
得

①如果方程(2)有2个实根(包括重根)在区间[0,1]内,那么
即
②如果方程(2)有1个实根在区间[0,1]内,另1个实根在区间[0,1]外,那么
f(0)f(1)≤0,
即

根据笔者的经验,能熟练掌握这种讨论并且运算不出错的学生很少.这样,一个原本不是很难的问题被化归为大部分高中学生不易解决的难题,因此这个解题思路方向并不能令人满意.
3 另一种解题思路
例1另解由0≤x≤1知
x-2<0,
从而

(3)

1≤|x-2|≤2,


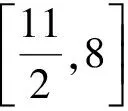
从而

此即为所求的函数值域.
在这一解法中,式(3)的代数变形能力要求稍高,如果遵循以下的问题化归思路,那么就会有章可循,十分自然了.
4 求二次分式函数值域的化归思路

(1)当a2=c2=0,b2≠0时,

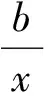


当且仅当x=1时,等号成立,且当x无限接近于0时,y无限增大,故y∈(1,+∞).
这是二次分式函数值域问题的最简单、基本的情形.以下讨论显示,除一些平凡的或者退化的情形外,其他情形均可化归为此类情形.
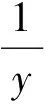

解(1)当x=0时,y=0;
(2)当x∈[-2,0)∪(0,2]时,由

得

从而

(3)当a2=0,b2≠0,c2≠0时,作变量代换u=b2x+c2,问题化归为情形(1).

解令x+4=t,则t∈[4,6],于是
(4)当a1=0,b1≠0,c1≠0时,作变量代换u=b1x+c1,问题化归为情形(2).

解令x-3=t,则t∈[-3,-1],于是
从而
(5)当a1a2≠0时,作以下变形:


则问题可化归为情形(4).例1就是这类情形的一个实例.
以上忽略了一些平凡和退化情形的讨论,最后对此作一个交代:
(6)当分子分母可约,或a1,a2同时为0时,函数可化为(或退化为)一次分式函数或常函数,一次分式函数均可利用图像平移化归为反比例函数.
(7)当a2=b2=0时,函数退化为二次函数,当a1=b1=0时,函数是二次函数与反比例函数的复合.


限于篇幅,对以上几种平凡和退化的情形不再举例说明.

