对三元均值不等式加强的一串演变

●

(咸阳师范学院基础教育课程研究中心 陕西咸阳 712000)

对三元均值不等式加强的一串演变

●安振平

(咸阳师范学院基础教育课程研究中心 陕西咸阳 712000)

《数学教学》1985年第3期上问题栏目的第73题为：

问题1若x,y,z为正数，求证：

x3+y3+z3≥ 3xyz+x(y-z)2+

y(z-x)2+z(x-y)2.

这显然是三元均值不等式的一个加强.对这个不等式进行变形可得1975年全苏数学奥林匹克竞赛十年级的第2题：

问题2对于正数x,y,z，有下述不等式成立:

x3+y3+z3+3xyz≥

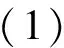
证明不妨假设x≥y≥z>0，则

(x-y)2(x+y-z)≥0,z(x-z)(y-z)≥0，

也就是

x3+y3+2xyz≥xy(x+y)+y2z+zx2,

z3+xyz≥yz2+xz2.

将这2个式子相加，即得不等式(1).

其实，不等式(1)还可以变形为:

问题3已知x,y,z为正数，求证：

xyz≥(y+z-x)(z+x-y)(x+y-z).

(2)

这是一道1983年瑞士数学竞赛试题.把不等式(2)进行变形，就有

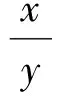
问题4设正数a,b,c满足abc=1，求证：

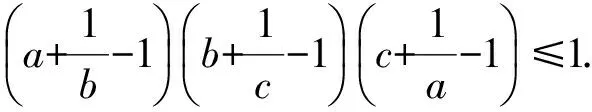
将问题2弱化，对不等式(1)的右边应用二元均值不等式，得

x3+y3+z3+3xyz≥

xy(x+y)+yz(y+z)+zx(z+x)≥

问题5对于正数a,b,c，有下述不等式成立:

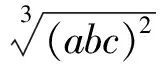
利用这个不等式，容易证明2004年亚太地区数学奥林匹克竞赛中的一道不等式题目：

问题6对于任意正实数a,b,c，均有

(a2+2)(b2+2)(c2+2)≥9(ab+bc+ca).

证明所证的不等式等价于

(abc)2+2(a2b2+b2c2+c2a2)+

4(a2+b2+c2)+8≥9(ab+bc+ca).

(4)

由二元和三元均值不等式,易证

2(a2b2+b2c2+c2a2)+6≥4(ab+bc+ca),

3(a2+b2+c2)≥3(ab+bc+ca)，

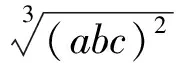
将以上3个不等式与不等式(3)的2边分别相加，立即得出不等式(4)，得证.

文献[2]将问题6加强为:

问题7对于任意正实数a,b,c，均有

证明所证的不等式等价于

(abc)2+ 2(a2b2+b2c2+c2a2)+(a2+b2+c2)+8≥

仿照问题6的证法，由二元和三元均值不等式，容易得到

2(a2b2+b2c2+c2a2)+6≥4(ab+bc+ca),

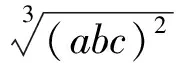
将以上2个不等式与不等式(3)的2边相加，立即得出不等式(6)，得证.

文献[3]将问题7进一步深化为：

问题8对于任意实数a,b,c及非负实数m，均有

问题9对于任意实数x,y,z,均有

问题10对于任意实数a,b,c,均有

(8)

证明注意到

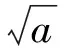
因此要证明不等式(8)，只要证明

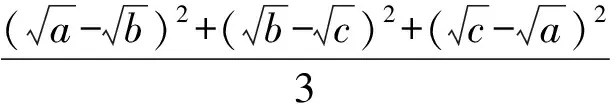
即

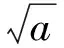
(本文为咸阳师范学院重点科研课题(08XSYK110)资助项目.)

[1] 安振平.三元均值不等式的加强及应用[J].中学数学教学参考,1998(10):40-41.

[2] 杨志明.两道赛题的统一加强[J].中学数学研究，2007(10):48-49.

[3] 杜旭安.一道竞赛题的加强与推广[J].数学通讯,2008(5):33.

[4] 罗增儒.数学解题学引理论[M].西安:陕西师范大学出版社，1997:228-329.