基于VB和Access的温度采集系统的设计与实现
宁必锋,苏 琪
(1.吉林化工学院 理学院,吉林 吉林 132022;2.吉林市第五中学 吉林 吉林 132022)
在工程设计、机械制造等许多领域中,求解全局优化问题的智能优化算法有粒子群优化算法、遗传算法等,笔者考虑使用粒子群优化算法。1995年,粒子群优化算法被美国的Kennedy和Eberhart首次提出后[1]在各个领域得到广泛的应用。目前产生了许多改进的粒子群优化算法。由于混沌具有遍历性、随机性等特点,许多学者提出了嵌入混沌序列的混合粒子群优化算法[2],这些算法在不同程度上改进了粒子群优化算法的收敛速度和解的精度。
笔者主要做了如下工作:1)首先将混沌序列初始化与粒子群优化算法充分结合,即在混沌初始化后,继续使用混沌序列产生新的粒子位置,使混沌序列遍历性得以充分利用。2)然后采用离差平方和法对粒子群进行聚类,同时根据粒子更新位置的目标函数适应值与个体和全局历史最好位置目标函数适应值进行比较,不同的类速度更新公式不同。提出基于离差平方和法的粒子群优化算法简称(CPSOW),并且给出了算法流程,通过3个标准测试函数的数值模拟实验,结果表明所提出的算法优于其它算法。
1 基于离差平方和法的粒子群优化算法
文中所要解决的全局连续优化问题[3]是

其中f(x)是一个实函数,x是一个实数向量。S={x∈S⊂Rn,aj≤xj≤bj; j=1…n}。
1.1 充分运用混沌序列遍历性质
笔者在算法的前期充分利用混沌序列均匀性、遍历性和随机性,避免了在算法后期搜索速度慢。文章采用的混沌序列迭代公式是典型的混沌动力学系统Logistic方程
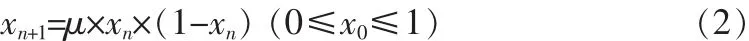
μ=4,x0∈(0,1) 随机数, 这里 x0是混沌序列的初始值,x0≠{0,0.25,0.5,0.75,1.0}。
事实上,首先根据Logistic方程迭代产生大量混沌序列后择优出初始化群体,其次混沌序列随着算法的循环继续根据Logistic方程进行迭代产生新的混沌序列,根据混沌序列遍历性和不重复性质,若是混沌序列产生的最优解位置比迄今为止粒子群搜索到的最优解位置还要好,就用这个位置替代粒子群中某一个粒子的位置。
1.2 离差平方和法
离差平方和法[4]是Ward在1936提出来的,也称为Ward法。它基于方差分析思想,如果类分的正确,则同类样品之间的离差平方和法应当较小,不同类的样品之间的离差平方和应当较大。
假定已将 n 个样品分为 m 类,记为 G1,G2,…,Gm,nw表示Gw类的样品个数,表示Gw的重心 (重心就是属于该类样品的均值)。 Xwi表示 Gw中第 i个样品(i=1,…,nw),则 Gw中样品的离差平方和为
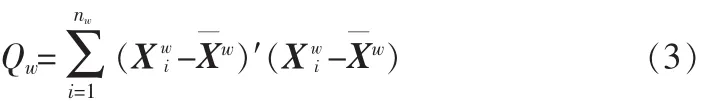
其中,Xwi,为 s维向量,Qw为一数值(w=1,2,…,m)。m个类的总离差平方和为

当m固定时,要选择使Q达到极小的分类。
Ward法的基本思想是,先将n个样品各自成一类,此时Q=0;然后每次将其中某两类合并为一类,因每缩小一类离差平方和就要增加,每次选择使Q增加最小的两类进行合并,直至所有的样品合并为一类为止。
1.3 粒子目标函数值分类过程
根据新粒子位置的目标函数值[5],可以将粒子分成3类,并由此改变粒子更新速度公式。
第一步:当搜索更新的粒子的目标函数适应值不如先前粒子最好个体的目标函数适应值时,符合以上条件的粒子用公式(5)来进行速度更新。用pbesti表示粒子本身所找到的最好解,叫做个体极值点。用gbesti表示整个种群目前找到的最好解,称为全局极值点。其中r1和r2是随机数,0≤r1≤1,0≤r2≤1;1≤i≤N,1≤j≤N;c1和 c2是加速因子,0 第二步:当搜索更新的粒子的目标函数适应值好于先前粒子最好个体的目标函数适应值,但是不如整个粒子群迄今为止搜索到的最优解的目标函数值时。用更新的粒子位置代替自己先前最好位置,符合以上条件的粒子用公式(6)来进行速度更新。,而且还要比较出这一类中目标函数适应值最好的粒子位置设为:pklc。 其中pklc表示第k代这个类中最优解的位置。 第三步:当搜索更新的粒子的目标函数适应值好于整个粒子群迄今为止搜索到的最优解的目标函数适应值时,并且在迭代公式(6)中粒子先前个体最好位置项依然应用,符合以上条件的粒子用公式(7)来进行速度更新,而且还要继续比较出这一类中目标函数适应值最好的粒子位置设为:pkgc。 其中pkgc表示第k代这个类中最优解的位置。 CPSOW算法步骤[3]如下: 1)初始化: 步骤1初始化迭代次数k=0、最大迭代次数kmax=3 000、维数n=50、种群个数N=30,利用混沌序列在n维问题空间中初始化N粒子的位置(xki,i=1,2…N)利用混沌序列在n维问题空间中初始化N粒子的速度(vki,i=1,2…N) 步骤2利用公式(1)计算每个粒子的目标函数值f(xki)。 步骤3初始化粒子的各自最好位置,预分配个体最好位置 pki=xki且 f(pki)=f(xki)(i=1,…N),初始化当前代全局最优解的位置,寻找 并且初始化pkg=pgkbest和 f(pkg)=f(pgkbest)。 2)优化过程(重复迭代直到满足停止循环的条件) 步骤1在当前代中继续计算初始化的混沌序列并且转化混沌序列为粒子的位置和速度。 步骤2执行离差平方和法聚类过程和粒子目标函数值分类过程,然后进行速度更新。 步骤3根据公式xki+1=xki+vki+1来更新粒子位置xki,根据公式(1)来计算每个粒子的目标函数值 f(xki)。 步骤4更新个体最好目标函数适应值:若是粒子的当前代目标函数适应值优于自己历史最好值,那么就用当前代粒子的位置代替先前粒子的位置;并且更新迄今为止全局最好目标函数适应值:比较所有粒子适应值,选取优于历史全局最好适应值的粒子位置替代先前全局最优解的粒子位置。 步骤5增加迭代步数 k=k+1。 3)停止迭代的条件被满足。全局最优解pkgbest和目标函数值 f(Pkgbest)。 文中采用文献[6]中3个标准测试函数:Sphere函数、Rosenbrock函数、Rastrigin函数来验证算法的性能,算法停止的两个标准:达到迭代的最大步数或者是达到最小误差限。为了评价基于混沌的聚类粒子群优化算法(CPSOW)的性能,采用了4种统计参数:最好值(最优解)、最优解的平均值、最优解的标准差、最优解满足精度所需要的步数,并且与标准粒子群优化算法(SPSO)、混沌粒子群优化算法(CPSO)、惯性权重线性递减粒子群优化算法 (LDIWPSO)进行比较分析。对于SPSO,CPSO,LDIWPSO 的参数设置分别参照了文献 [7]、[8]。运用软件MATLAB(Version7.4)进行模拟数值实验,实验进行100次,表中粗体数值表示同类别数据中最好者。 根据表1~表3主要的分析和比较如下: 表1 Sphere函数各算法的比较结果Tab.1 Resu lts com parision of four algorithm s for Sphere function 表2 Rosenbrock函数各算法的比较结果Tab.2 Results comparision of four algorithms for Rosenbrock function 表3 Rastrigin函数各算法的比较结果Tab.3 Results comparision of four algorithms for Rastrigin function 图1 Sphere函数最好解函数适应值变化趋势图Fig.1 Comparison of best fitness trendlines for the Sphere function 图3 Rastrigin函数最好解函数适应值变化趋Fig.3 Comparison of best fitness trendlines for the Rastrigin function 图2 Rosenbrock函数最好解函数适应值变化趋势图Fig.2 Comparison of best fitness trendlines for the Rosenbrock function 1)在所有函数优化问题测试中,CPSOW算法都提高了最优解的精度,在函数Sphere,Rastrigin比较中CPSOW算法最优解的精度提高的均很显著,已经达到10-29~10-9之间,这说明所提算法的搜索能力强,并能够使算法收敛到目标函数的理论极值点。 2)在最优解的标准差比较中,在函数Sphere,Rastrigin中CPSOW算法的结果相当好,精度已经分别达到10-27~10-9。由此验证了在算法中,根据粒子位置采用不同速度更新公式,由此不断靠近全局最优解,因此从数据结果来看,所提出的CPSOW算法,实验结果波动性比较小。 3)从图1到图3可知:CPSOW算法在所有测试函数中,最优解函数适应值均始终保持最好,而在Sphere函数和Rosenbrock函数中搜索最优解速度极快,百步之内就能迅速定位全局最优解的所在空间区域,这说明在CPSOW算法中充分利用混沌序列的均匀性和遍历性,为粒子发现全局最优解位置提供重要的信息,致使粒子快速靠近全局最优解,从而CPSOW算法始终保持最好的结果。 文中提出了基于离差平方和法的粒子群优化算法,该算法在应用混沌序列的遍历性和随机性,使得CPSOW算法能够避免无用的搜索,缩短寻优时间。然后采用离差平方和法进行聚类提高寻找最优解的能力。同时根据粒子更新位置的目标函数适应值与个体和全局历史最好位置目标函数适应值进行比较分类,进行速度更新。应用所提出的算法处理3个典型优化函数,并与3种算法SPSO,CPSO,LDIWPSO进行比较分析。实验数据结果表明:CPSOW算法不易受早熟影响,几乎不陷入局部最优解中,不论是算法搜索最优解的速度,还是在最优解的精度,CPSOW算法都有所的提高。 [1]Kennedy J,Eberhart R C.Particle swarm optimization[C]//In:Proceedings of IEEE International Conference on Neural Networks,Piscataway:IEEE Service Center,1995:1942-1948. [2]LIU Bo,WANG Ling,JIN Yi-hui,et al.Improve particle swarm optimization combined with chaos[J].Chaos Solitons and Fractals,2005(25):1 261-1 271. [3]钱伟懿,宁必锋.基于混沌的聚类粒子群优化算法[J].计算机工程与设计:2011,32(2):685-688.QIAN Wei-yi,NING Bi-feng.Clustering particle swarm optimization algorithm based on chaos[J].Computer Engineering and Design,2011,32(2):685-688. [4]高惠璇.应用多元统计分析 [M].北京:北京大学出版社,2009. [5]宁必锋,褚国娟,马春丽,等.一种改进的混合粒子群优化算法[J].渤海大学学报:自然科学版,2010,31(1):37-43.NING Bi-feng,CHU Guo-juan,MA Cun-li,et al.An improved hybrid particle swarm optimization algorithm[J].Journal of Bohai University:Natural Science Edition,2010,31(1):37-43. [6]Arumugam MS,Rao MV C,Chandramohan A.A new and improved version of particle swarm optimization algorithm with global-local best parameters[C]//Knowl Inf Syst,2008:331-357. [7]纪震,廖惠连,吴青华.粒子群算法及应用[M].北京:科学出版社,2009. [8]Alatas B,Akin E,Ozer A B.Chaos embedded particle swarm optimization algorithms[J].Chaos,Solitons and Fractals,2009,40(4):1715-1734.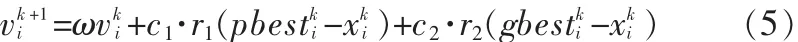
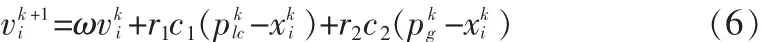

2 文中提出的算法流程
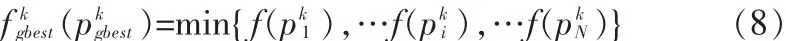
3 算法仿真实验与比较研究
4 实验结果分析






5 结束语

