不确定系统响应上下界分析的改进仿射算法

谢永强，陈建军，朱增青

(西安电子科技大学机电工程学院 西安 710071)

不确定系统响应上下界分析的改进仿射算法

谢永强，陈建军，朱增青

(西安电子科技大学机电工程学院 西安 710071)

针对仿射运算时新符号噪声的引入必然造成误差放大的不足，在函数上下界计算中引入了矩阵形式的上下界的仿射计算公式，提出了一种计算上下界的改进仿射算法。该算法在仿射变量进行乘法运算时不会引入新的噪声，相对与传统的仿射算法能得到更紧凑的界限；并通过实例计算演示了该公式的计算过程及计算方法的有效性。将有界不确定性变量的仿射型及改进的仿射运算引入不确定系统响应上下界的计算。仿真结果表明，相对于区间算法及传统的仿射算法，该算法得到解的界限更为紧凑。

仿射型; 区间算法; 改进的仿射算法; 不确定系统

对不确定系统响应的上下界求取常采用区间算法和仿射算法。当已知信息较少，如只能获得变量的上下界时，可以采用区间算法。由于区间运算(interval arithmetic, IA)规则的不合理性[1-2]，导致了区间运算结果极易扩张和溢出。当函数嵌套较深或为强非线性函数时，误差爆炸(error explosion)的强度越大，导致计算所得的变量界限毫无意义。完全忽略变量之间的相关性，以及对数、开方等运算的圆整误差(round off error)和倒数运算的溢出误差(over shoot error)是误差爆炸的直接原因[3]。

仿射型及仿射运算(affine arithmetic，AA)[3]是处理不确定性问题的新方法，已应用在电路响应界分析[4-5]、系统稳定性分析[6]、人工智能系统分析[7]及计算机图形学[2,8]中。AA将确定性变量的仿射型用噪声的线性组合表示，若多个仿射型拥有同一噪声符号，则二者具有相关性[1]；且拥有相同噪声符号的数目越多，仿射型之间的相关性越大[3]。该性质使AA能表示变量之间的相关性，加之运算规则具有优化性质，使其运算精度远高于区间运算，能被应用于众多的领域中。然而，由于仿射运算优化逼近的存在，使AA不可避免地会存在误差，例如两个仿射型的乘积运算中新噪声的引入，就是对乘积中噪声二次项的近似逼近。基于文献[9]的证明，结合仿射型的特性，本文提出了多项式矩阵形式的上下界的改进仿射计算公式，该公式不需要导数信息，在仿射变量进行乘法运算时不会引入新的噪声，能够求得更精确的上下界。本文用该公式分析了多变量作用下的不确定系统，求出了不确定系统的响应上下界，与区间算法和传统的仿射算法相比，该算法得出的结果更紧凑，更接近系统响应的真实值。

1 不确定性量的仿射型和仿射算法

1.1 仿射型与区间变量

设由于自身或环境原因有t种噪声共同影响不确定性量的真值，则其仿射型ˆx表示为t个噪声符号的一次多项式[1]：

1.2 仿射运算规则

图1 倒数运算的仿射拟合

2 二元区间多项式上下界公式和改进的仿射算法

尽管AA比区间运算有更高的精度，但由于在非线性仿射运算中采用了近似逼近，使非线性AA的误差会随着非线性程度的增高而加剧。为了进一步减小这些非线性运算带来的误差，本文提出了多项式矩阵形式的上下界的改进仿射计算算法(modified affine arithmetic，MAA)。

2.1 二元区间多项式的上下界公式

针对仿射运算中的乘法运算公式带来的误差，文献[9]给出矩阵形式二元区间多项式上下界公式，能更精确地计算出区间多项式的上下界。设二元区间多项式为:

2.2 改进的仿射算法

除了AA的乘法运算，其他的非线性运算也会在仿射运算过程中引入新的误差。对非线性运算的仿射算法常采用切比雪夫近似，文献[1]提出了AA中非线性运算的切比雪夫算法。

图2 区间减小仿射误差减小

由定理1及定理2可知，如果在进行倒数仿射拟合时能缩小近似区间的范围，就可以减小仿射近似时带来的误差。

3 系统响应界分析的改进仿射算法

针对不确定系统响应界的分析，常采用区间算法来处理[10-13]。文献[11]将区间分析理论应用于不确定参数的控制问题，通过独立模态控制得到闭环系统，并提出了估计响应上下界的计算方法。文献[10]在已知滞回环本身不确定因子的区间中点和半径的前提下，推导得到不确定响应的区间分布。当只能得到不确定参数的上下界时，用区间方法可以得到系统的响应界限。当影响系统的噪声有多个，且对系统参数的影响为深度嵌套的隐函数时，直接利用区间方法将系统参数的上下界代入，所求得的响应区间往往远大于真实值。为了减小系统响应界的计算误差，可以在界计算中利用本文的改进仿射算法，对不确定系统的响应界进行分析。

3.1 确定性系统的响应

确定性系统的传递函数的一般形式为：

高阶系统的响应由一阶和二阶系统的时间响应函数组成。

3.2 不确定性系统的响应上下界的改进仿射分析

当系统中有不确定变量且变量可表示为仿射形式时，控制系统的传递函数可用下式描述为：

对上式响应的上下界进行分析时，可以参考确定系统响应的求法，并在计算不确定变量时引入改进的仿射算法，其步骤如下：

1)利用符号运算工具，将系统响应函数的分母部分进行因式分解，得到不确定系统极点的仿射形式，则系统的响应函数为：

该运算为含仿射变量的仿射运算，为了得到更精确的解，可利用本文改进的仿射算法进行计算。由于在计算各系数时只用到了仿射算法的乘法运算和倒数运算的仿射拟合，由定理1和定理2可证明改进的仿射运算得到的各系数的解区间更为紧凑。

当系统中有二阶环节时，响应中一般有正弦量，响应的上下界难以确定，但响应包络线的上下界仍然可由下式确定为：

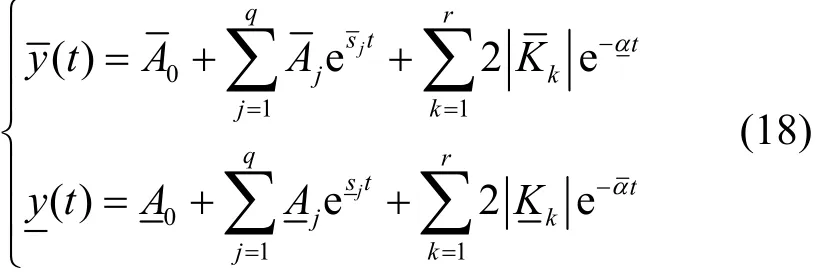
以上算式中变量的上下界可利用改进的仿射变量上下界公式进行计算，可以得到比传统的仿射算法和区间算法更为紧凑的上下界区间。

4 算 例

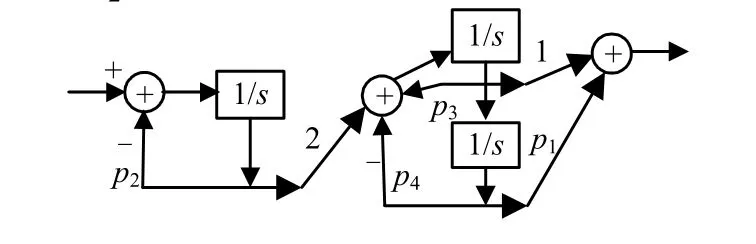
图3 含不确定参数的系统

可得系统响应上下界曲线，并显示了随机取121个不确定变量对(e1,e2)后系统的响应曲线，如图4所示。

图4 不确定系统响应及上下界

图5所示为在6～10 s时系统的响应。从图4和图5中可以看出，当参数对(e1,e2)变化时，系统的响应也随之变化，但其变化范围总是落在求得的响应界曲线的范围内。

图5 系统在6～10 s时的响应图

例2 二阶RLC电路如图6所示，工作环境温度为20±20 ℃。在20 ℃时测量知电阻R=5 Ω，温度系数为0.004；电感L=1 H，温度系数为0.000 14；电容C=1 F，温度系数为−0.000 12。求系统在该温度范围内工作时的阶跃响应界限。

图6 二阶RLC电路

图7 3种方法得到的响应界限

图7所示为用3种方法得到的系统响应界限图，并显示了随机取125个不同温度时系统的实际响应曲线。由图中可以看出，用本文改进的仿射算法得到的系统响应界限最为紧凑，传统的仿射算法次之，用区间算法得到的响应界限最宽，与系统的真实响应界限相差较大。

5 结 论

本文针对仿射运算的误差原因进行了分析，提出了一种函数上下界计算的改进仿射算法，将有界不确定性变量的仿射型及改进的仿射运算引入到不确定系统响应上下界的计算中，并对该算法的精确性进行了证明。最后通过实例计算演示了该公式的计算过程及计算方法的有效性。仿真结果表明，相对于区间算法及传统的仿射算法，该算法得到的解的界限更为紧凑。该算法的提出有助于对系统响应界做更精确的分析。

[1]STOLFI J, HENRIQUE L F. Self-validated numerical methods and applications[M]. [S.l.]: Monograph for 21st Brazilian Mathematics Colloquium, 1999.

[2]SHOU H, MARTIN R, VOICULESCU I, et al. Affine arithmetic in matrix form for polynomial evaluation and algebraic curve drawing[J]. Progress in Natural Science,2002, 12(1): 77-80.

[3]HENRIQUE DE FIGUEIREDO L, STOLFI J. Affine arithmetic: concepts and applications[J]. Numerical Algorithms, 2004, 37: 147-158.

[4]GRIMM C, HEUPKE W, WALDSCHMIDT K. Analysis of mixed-signal systems with affine arithmetic[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2005, 24(1): 118-123.

[5]FEMIA N, SPAGNUOLO G. True worst-case circuit tolerance analysis using genetic algorithms and affine arithmetic[J]. IEEE Transactions on Circuits and Systems,2000, 47(9): 1285-1296.

[6]谢永强，陈建军. 不确定系统稳定性的仿射不等式分析[J].高技术通讯，2008, (4): 867-871.

XIE Yong-qiang, CHEN Jian-jun. Stability analysis of uncertain system using affine inequality[J]. Chinese High Technology Letters, 2008, (4): 867-871.

[7]GOLDENSTEIN K S, VOGLER C, METAXAS D.Statistical cue integration in DAG deformable models[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(7): 801-813.

[8]MARTIN R, SHOU Hua-hao, VOICULESCU I, et al.Comparison of interval methods for plotting algebraic curves[J]. Computer Aided Geometric Design, 2002, 19:553-587.

[9]SHOU Hua-hao, LIN Hong-wei, MARTIN R, et al.Modified affine arithmetic is more accurate than centered interval arithmetic or affine arithmetic[M]. Berlin: [s.n.],2003: 355-365.

[10]邱志平，顾笑冬，李登峰. 单自由度不确定滞回系统振动响应的区间分析方法[J]. 动力学与控制学报, 2007,5(2): 173-177.

QIU Zhi-ping, GU Xiao-dong, LI Deng-feng. Viberation analysis on uncertain single-degree-of-freedom hysteretic system using interval analysis method[J]. Journal of Dynamics and Control, 2007, 5(2): 173-177.

[11]陈塑寰，裴春艳. 不确定二阶振动控制系统动力响应的区间方法[J], 吉林大学学报(工学版), 2008, 38(1): 94-98.

CHEN Su-huan, PEI Chun-yan. Dynamic response of second-order uncertain vibration control systems with interval method[J]. Journal of Jilin University (Engineering and Technology Edition), 2008, 38(1): 94-98.

[12]邱志平，马丽红，王晓军. 不确定非线性结构动力响应的区间分析方法[J]. 力学学报, 2006, 38(5): 645-651.

QIU Zhi-ping, MA Li-hong, WANG Xiao-jun. Interval analysis for dynamic response of nonlinear structures with uncertainties[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(5): 645-651.

[13]林立广, 陈建军, 马娟. 基于区间因子法的不确定性桁架结构动力响应分析[J]. 应用力学学报, 2008, 25(4):612-617.

LIN Li-guang, CHEN Jian-jun, MA Juan. Dynamic response analysis for uncertainty truss structures with interval factor method[J]. Chinese Journal of Applied Mechanics, 2008, 25(4): 612-617.

编 辑 黄 莘

Uncertain System Response Bounds Analysis with Modified Affine Arithmetic

XIE Yong-qiang, CHEN Jian-jun, and ZHU Zeng-qing

(School of Electromechanical Engineering, Xidian University Xi´an 710071)

The introduction of new noise symbols causes error amplification in affine arithmetic inevitably.To avoid this disadvantage, this paper presents a modified affine arithmetic in matrix form for bounds computation of functions. The modified affine arithmetic does not introduce new noises during multiplication operation of affine variables, and it can obtain compacter bounds compared with conventional affine arithmetic. The formulas computing processes and the validity of proposed method are demonstrated by an example. The affine form of bounded uncertain variables and modified affine arithmetic are used to calculate response bounds of uncertain system. The simulations show that, the proposed approach can obtain closer response bounds than interval arithmetic and conventional affine arithmetic.

affine form; interval arithmetic; modified affine arithmetic; uncertain system

TP202; O242

A

10.3969/j.issn.1001-0548.2011.03.033

2009- 09- 23;

2011- 04- 27

国家863计划(2006AA04Z402)

谢永强(1976- )，男，博士生，主要从事不确定系统分析与控制方面的研究.