二阶脉冲微分方程组四点边值问题非负解的存在性

卢振花, 刘锡平, 沈 立

(上海理工大学理学院,上海 200093)

1 问题的提出

微分方程组理论是研究高阶微分方程相关问题的重要基础,近年来,常微分方程组的理论研究受到了国内外学者的广泛关注[1-3].文献[2]利用Leggett-Williams不动点定理研究了一类二阶微分方程组两点边值问题解的存在性,得到了非负解存在的充分条件.众所周知,脉冲微分方程在电子工程和生物工程等领域有着广泛的应用背景,国内外学者对脉冲微分方程边值问题进行了大量研究[4-5].文献[4]利用Leggett-Williams不动点定理研究了一类二阶脉冲微分方程三点边值问题非负解的存在性.文献[5]研究了一类二阶脉冲微分方程积分边值问题的存在性和唯一性.

本文研究二阶脉冲微分方程组四点边值问题

非负解的存在性.其中,fi∈C([0,1]×R+×R+,R+),Ii k∈C(R+×R+,R+),R+=[0,+∞),0＜t1＜t2＜…＜tm＜(tk).xi(tk),xi(t+k)分别为xi(t)在t=tk处的左、右极限,关于x′i(t)有类似的定义,i=1,2.

令J=[0,1],J′=J{t1,t2,…,tm},PC[J, R]={x∶J→R∶x(t)在t≠tk连续,x(tk), x(t+k)均存在,且满足x(tk)=x(tk),k=1,2,…,m}.

设E=PC(J,R),‖x‖0=supt∈[0,1]｜x(t)｜,则(E,‖◦‖0)是Banach空间.设X=E×E,并取范数‖(x1,x2)‖=‖x1‖0+‖x2‖0,则(X,‖◦‖)为Banach空间.

2 预备知识

引理1 设y∈C(J),0＜a＜1,则脉冲微分方程边值问题

的解x(t)当且仅当满足积分方程

其中

证明 假设x(t)是方程(2)的解,则存在ξk∈(tk-h,tk),使得

其中,0＜h＜tk-tk-1.

设x′(tk)=x′(tk),k=1,2,…,m.易得对任意t∈J,有

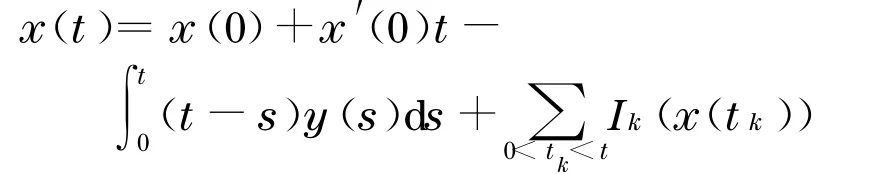
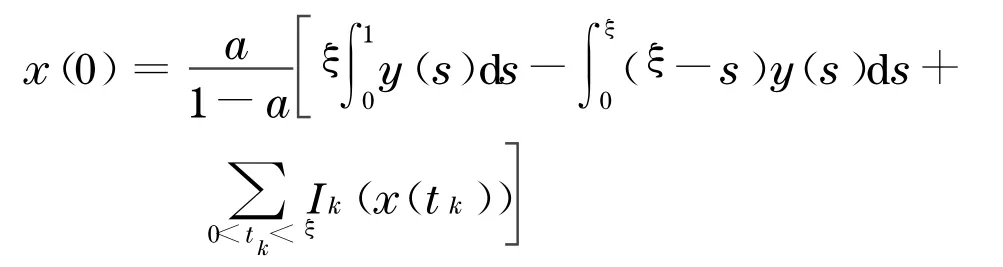
于是

当t≤ξ时

当t≥ξ时

那么任意t∈J,有

另一方面,若x∈PC[J,R]是积分方程的解,那么很容易得到x∈PC[J,R]∩C2[J′,R]是边值问题(2)的解.证毕.

定义算子T1,T2∶X→E.

其中

根据Gi(t,s)的定义,不难证明Gi(t,s)具有下面引理2的性质.

引理2 函数Gi(t,s)∈C([0,1]×[0,1]),i =1,2,并且

现给出Leggett-Williams不动点定理.

设常数d,L,r＞0,记

引理3[6]设E是一个Banach空间,K⊂X是X上的锥,c＞0,c为常数,若存在K上的非负连续凹泛函w,对任意x∈有w(x)≤‖x‖,并设是全连续算子,如果存在常数r,L和d满足0＜r＜L＜d≤c,使得下列条件成立:

a.{x∈K(w,L,d)∶w(x)＞L}≠Ø,并且对任意x∈K(w,L,d),有w(Tx)＞L;

c.对任意x∈K(w,L,c),当‖Tx‖＞d时,有w(Tx)＞L.

3 主要结论及其证明

令K={(x1,x2)∈X∶xi(t)≥0,t∈[0,1],i= 1,2},则K为X上的锥.定义

其中,1＞δ＞max{tm,ξ1,ξ2},x∈K.那么易得w是K上的非负连续凹泛函.

记D=[0,1]×[0,+∞)×[0,+∞),a0= min{a1,a2},ξ0=min{ξ1,ξ2}.

定理1 若存在正常数r,L,d,c,λi,λ′i,μi,μ′i,i =1,2,满足λ1+λ2=1,λ′1+λ′2=1,μ′1+μ′2=1,r＜并且下列条件成立:

a.对任意(t,u,v)∈{(t,u,v)∈D∶u+v≤c},有

b.对任意(t,u,v)∈{(t,u,v)∈D∶u+v≤r},有

c.对任意(t,u,v)∈{(t,u,v)∈D∶L≤u+ v≤d,t∈[δ,1]},有i=1,2.

则边值问题(1)至少存在3个非负解,x*= (x*1(t),x*2(t)),y*=(y*1(t),y*2(t)),z*= (z*1(t),z*2(t)),且满足

且

且

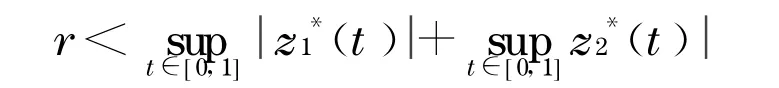
证明 设T∶X→X,T(x1,x2)=(T1(x1, x2),T2(x1,x2)).首先证明算子是全连续算子.

任意x=(x1,x2)∈K,由算子定义易得(Tix)(t)≥0,t∈[0,1],即Tx∈K,则T(K)⊂K.

由于定理限定条件λ1+λ2=1,λ′1+λ′2=1,则对任意x=(x1,x2)∈,有

现证明T满足引理3的条件.

类似于上面的证明过程,由定理1的条件b可得,对任意x=(x1,x2)∈,有‖Tx‖＜r.即引理3的条件b满足.

注意到 0＜a1,a2＜1,0＜ξ0＜1,则 0＜max{a1,a2}ξ0＜1,于是,有

即y0∈{x∈K(w,L,d)∶w(x)＞L}≠Ø.

对任意x=(x1,x2)∈K(w,L,d)有w(x)≥L,‖x‖≤d,即 L≤x1(t)+x2(t)≤d,t∈[δ,1]

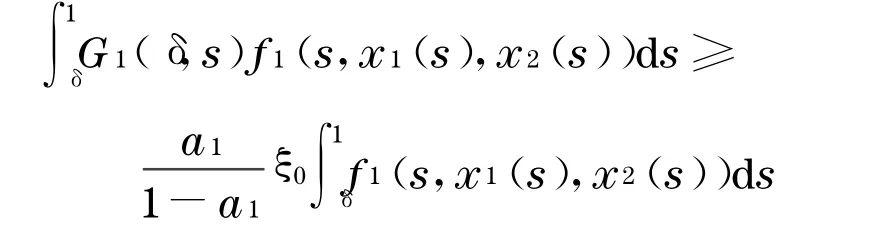
由定理1的条件c,有

由引理2,任意x=(x1,x2)∈K(w,L,d)且‖T x‖＞d时

因此,任意x∈K(w,L,d)且‖Tx‖＞d时,有 w(Tx)＞L.则引理3的条件c满足.

于是,边值问题(1)至少存在3个非负解x*= (x*1(t),x*2(t)),y*=(y*1(t),y*2(t)),z*= (z*1(t),z*2(t)),且满足定理结论.证毕.

[1] AGARWAL R P,O'REGAN D.A coupled system of differential equations[J].Math Comput,2000,114(1): 39-49.

[2] AGARWAL R P,O'REGAN D.A multiplicity result for second order impulsive differential equations via the Leggett Williams fixed point theorem[J].Appl Math Comput,2005,161(2):433-439.

[3] 席守亮,贾梅,纪慧鹏.二阶常微分方程组边值问题正解的存在性[J].上海理工大学学报,2009,31(4): 318-321.

[4] JIA Mei,LIU Xi-ping.Three nonnegative solutions of three-po intb oundary value problem forsecond-order impulsive differential equantions[J].Jo urnal of Mathematical Research and Exposition,2008,28(3): 567-574.

[5] JIA Mei,LIU Xi-ping.Existenceofsolutionsfor second-order impulsive differentialequations with integral boundary conditions[C]//Proceedings of the 7th Conference on Biological Dynamic System and Stability ofDifferentialEquation.Liverpool:World Academic Press,2009:2880-2886.

[6] GUO Da-jun,LAKSHMILKANTHAM V.Nonlinear Problemsin Abstract Cones[M].San Diego:Academic Press,1988.