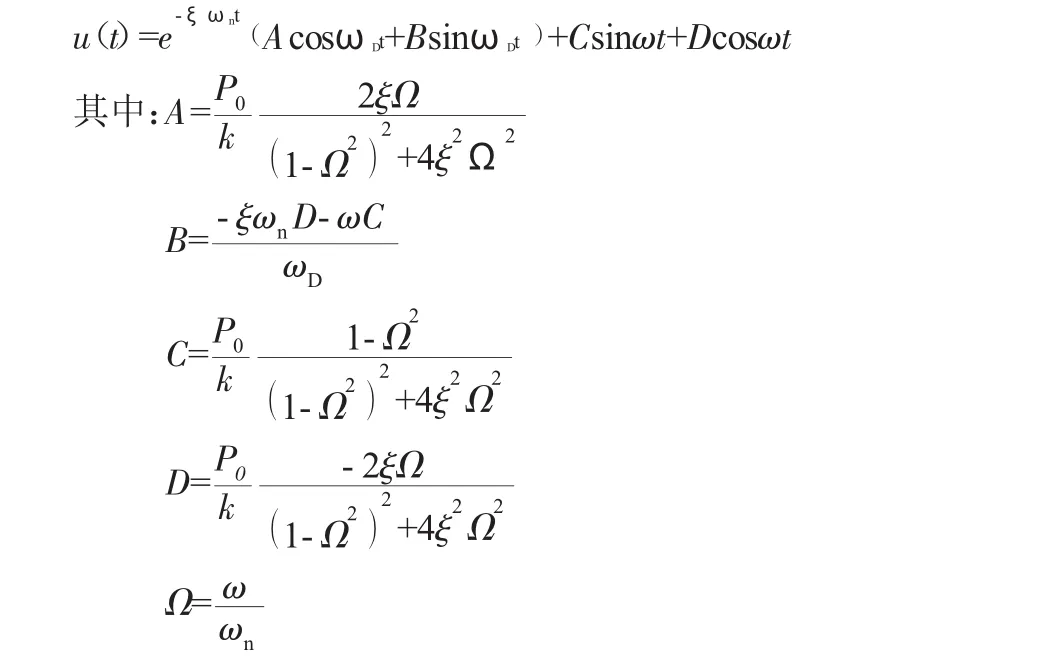数值计算求解非线性动力方程

郭 冲

（山西省公路局长治分局勘测设计所，山西 长治 046000）

1 引言

如果外荷载或者结构的刚度、质量、阻尼等任何一项随时间变化，那么这样的结构体系就是非线性的，这种结构体系的动力方程也是非线性的。对于此类非线性动力方程，其解析解往往较难由理论推导得到，这类问题可以通过数值计算方法对动力响应方程进行求解。常用的数值计算方法包括激励线性插值法、中心差分法、Newmark的平均加速度法和线性加速度法等。

2 各数值算法的基本原理

2.1 激励线性插值法

对于线性体系，通过在每个时间间隔里对激励进行插值，并利用线性体系响应解析解，能够推导出一种有效的数值计算方法。只要保证插值的时间间隔较短，就可以得到令人满意的求解结果。

对于欠阻尼体系（ξ＜1），有非线性动力方程

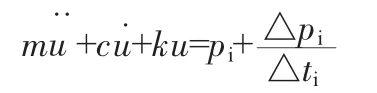
在时间间隔0≤τ≤△ti内，反应u（τ）由3部分组成：

（1）τ=0时刻的初位移ui和初速度u觶i引起的自由振动响应；

（2）零初始条件下对阶跃力pi的反应；

（3）零初始条件下对斜坡力（△pi/△ti）τ的反应。

经推导可得出第i+1个时间步的位移与速度公式如下：

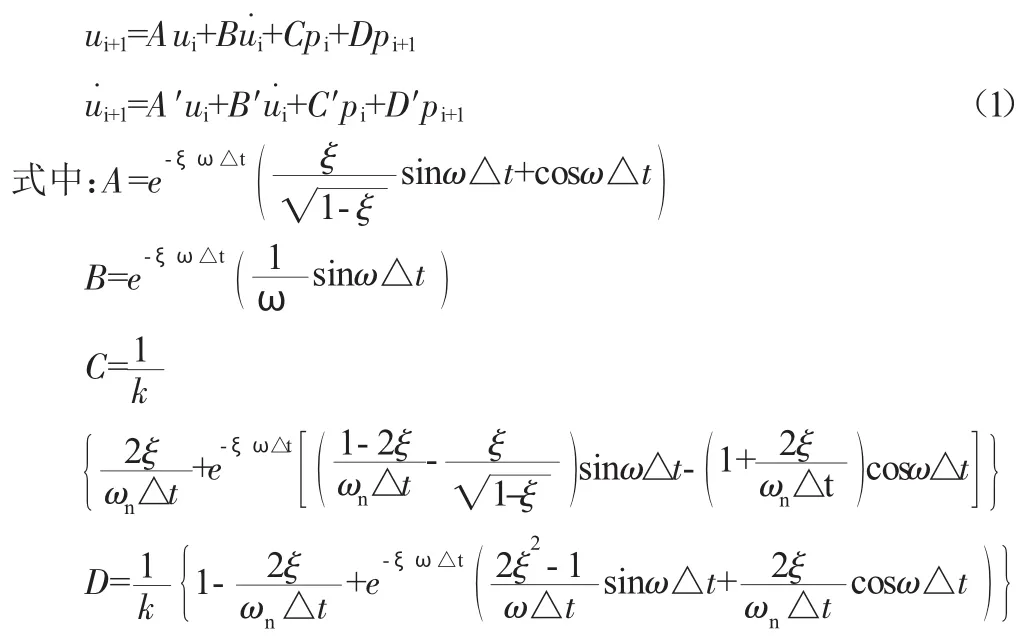
ω：外荷载频率；

ωn：结构固有频率。

给定初始条件，代入式（1）即可得到结构在任意时刻的响应。

2.2 中心差分法

该方法是基于对位移时间导数的有限差分近似进行的。取固定的时间步长△t，则时刻i的速度和加速度的中心差分格式为：

将上式的速度加速度代入动力方程中得：

为了计算ui+1，需要知道位移ui和ui-1。若已知初始位移u0，则u-1可表示为：

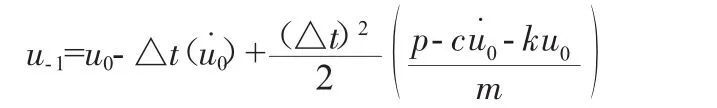
至此，所有参数均可以通过初始条件与公式进行递推求得，则任意时刻的结构响应可以通过数值计算得到。

2.3 Newmark法

N.M.Newmark发展了一类时间步进法，它们基于下面的公式：

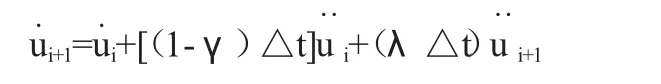
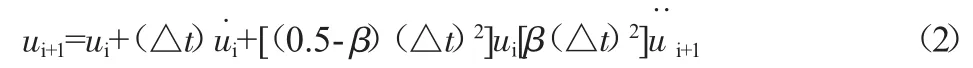
当 γ=0.5，β=0.25时，上式为平均加速度法；当 γ=0.5， β=1/6时，上式为线性加速度法。对式（2）以增量格式重写如下：

3 程序实现

上文对激励线性插值法、中心差分法与Newmark法的基本原理进行了介绍，借助数学计算软件Matlab，对这几种方法编制了相应的计算程序。现将Matlab中编制的函数展示如下。

3.1 激励线性插值法

function y=excitation（m，k，Tn，e，dt，t，F，te）

a=[0：dt：t]；n=length（a）；

for j=1：n

if a（j）

p（j）=F.*sin（pi.*a（j）./te）；

else

p（j）=0；

end

end

Wn=2.*pi./Tn；Wd=Wn.*（1-e.^2）.^0.5；

Si=sin（Wd.*dt）；Co=cos（Wd.*dt）；

E=exp（-e.*Wn.*dt）；

A=E.*（（e./（1-e.^2）.^0.5）.*Si+Co）；

B=E.*（Si./Wd）；

C=（2.*e./（Wn*dt）+E.*（（（1-2.*e.^2）./（Wd.*dt）-（e./（1-e.^2）.^0.5））.*Si-（1+2*e./（Wn*dt））.*Co））/k；

D=（1-2.*e./（Wn*dt）+E.*（（2.*e^2-1）./（Wd.*dt）.*Si+2.*e.*Co./（Wn.*dt）））./k；

At=-E.*（Wn./（（1-e.^2）.^0.5）.*Si）；Bt=E.*（Co-（e./（1-e.^2）.^0.5）.*Si）；

Ct=（-1./dt+E.*（（Wn./（（1-e.^2）.^0.5）+（e./（dt.*（1-e.^2）.^0.5））.*Si+Co./dt））/k；

Dt=（1-E.*（（e./（1-e.^2）.^0.5）.*Si+Co））./（k.*dt）；u（1）=0；ut（1）=0；

for i=2：n

u（i）=A.*u（i-1）+B.*ut（i-1）+C.*p（i-1）+D.*p（i）；

ut（i）=At.*u（i-1）+Bt.*ut（i-1）+Ct.*p（i-1）+Dt.*p（i）；

end

x1=[0：dt：t]；m=length（x1）；

y1=zeros（m，1）；y2=zeros（m，1）；

for i=1：n

y1（i）=u（i）；

y2（i）=ut（i）；

end

3.2 中心差分法

function difference（m，k，c，u0，ut0，dt，t，te，Tn）

if dt<（Tn./pi）

u（2）=u0；ut（2）=ut0；x=[0：dt：t]；n=length（x）；

for j=2：n+1

if x（j-1）

p（j）=10.*sin（pi.*x（j-1）./te）；

else

p（j）=0；

end

end

utt（2）=（p（2）-c.*ut（2）-k.*u（2））./m；

u（1）=u（2）-（dt）.*ut（2）+（dt）.^2./2.*utt（2）；

kt=m./（dt）^2+c./（2.*dt）；

a=m./（dt）^2-c./（2*dt）；b=k-2.*m./（dt）^2；

for i=2：n+1

pt（i）=p（i）-a.*u（i-1）-b.*u（i）；

u（i+1）=pt（i）./kt；

end

x1=[0：dt：t]；y1=zeros（n，1）；

for j=1：n

y1（j）=u（j+1）；end

3.3 Newmark法（线性加速度法）

function liner（m，k，c，u0，ut0，dt，t，te）

bet=1/6；gama=1/2；u（1）=u0；ut（1）=ut0；

x=[0：dt：t]；n=length（x）；

for j=1：n

if x（j）

p（j）=10.*sin（pi.*x（j）./te）；

else

p（j）=0；

end

end

utt（1）=（p（1）-c.*u（1）-k.*u（1））./m

kt=k+（gama./bet）./dt.*c+（1./bet）./（dt）^2.*m

a=1./（bet.*dt）.*m+（gama./bet）.*c

b=1./（2.*bet）.*m+dt.*（gama./（2.*bet）-1）.*c

for i=1：n-1

dp（i）=p（i+1）-p（i）；

dpt（i）=dp（i）+a.*ut（i）+b.*utt（i）；

du（i）=dpt（i）./kt；

dut（i）=（gama./bet）.*du（i）./dt-（gama./bet）.*ut（i）+dt.*（1-（gama./bet./2））.*utt（i）；

dutt（i）=（1./bet）./（dt）^2.*du（i）-（1./bet）./dt.*ut（i）-（1./bet./2）.*utt（i）；

u（i+1）=u（i）+du（i）；

ut（i+1）=ut（i）+dut（i）；

utt（i+1）=utt（i）+dutt（i）；

end

x1=[0：dt：t]；m=length（x1）；y2=zeros（m，1）；

图1 理论解与数值计算结果对比

for i=1：n

y2（i）=u（i）；end

4 求解实例

计算实例如下：单自由度体系具有如下特性：m=0.253 3千磅力·秒2/英寸、k=10千磅力/英寸、Tn=1 s（ωn=6.283弧度/s），ξ=0.05。试确定体系在正弦脉冲力p（t）=10sin（πt/0.6）作用下1s内的反应（△t=0.05 s），图1给出了理论解与数值计算结果对比。

为验证求解结果的正确性，首先给出该体系在正弦脉冲作用时间1 s内的理论解：

[1]唐友刚.高等结构动力学[M].天津：天津大学出版社，2002.

[2]吕同富，康兆敏，方秀男.数值计算方法[M]，北京：清华大学出版社，2009.

[3]邢棉.MATLAB数值计算在高等数学教学中的应用探讨[J].中国科教创新导刊，2010.

[4]李初晔，王增新.结构动力学方程的显式与隐式数值计算[J].航空计算科学，2010，01.