基于TFT-LCD的动态星模拟器星点位置修正方法
基于TFT-LCD的动态星模拟器星点位置修正方法
介绍了基于TFT-LCD的动态星模拟器的工作原理及星点位置误差的计算方法。利用经纬仪对动态星模拟器显示的网格星点进行测量,计算了各星点的位置误差及修正系数。对网格上星点的修正系数进行分区处理,并利用Matlab软件对各分区的修正系数进行曲线拟合,得到修正系数关于星点位置(方位或俯仰)坐标的方程。结果表明,修正后星点的位置误差均小于35″,满足动态星模拟器的设计要求。
动态星模拟器;经纬仪;曲线拟合
1 引 言
动态星模拟器是一种星敏感器的地面检测标定设备,在星敏感器的检测与标定过程中起着重要作用。动态星模拟器能够模拟无穷远处恒星组成的星图,能够显示不同恒星的位置及星等。星敏感器通过观察动态星模拟器显示的星图,实现对自身的星图识别和星跟踪等功能的检测。因此,动态星模拟器显示星图的准确程度直接影响了星敏感器检测的准确程度[1,2]。
动态星模拟器主要由星点显示器和准直光学系统两部分组成。通过星点显示器显示出来的星点经过准直光学系统后,远离中心点显示的星点会产生一定的像差,因此要对经过光学系统后的星点位置进行测量,然后对星点在原始坐标系中的输入坐标进行修正,使其经过光学系统后的位置与理论值的误差在允许范围之内[3,4]。
2 工作原理
动态星模拟器的工作原理如图1所示。TFTLCD显示器放在准直光学系统的焦平面上,且光学系统的轴心与TFT-LCD显示器所使用的视场中心重合。背光板发出的光均匀照射到TFT-LCD显示器上,TFT-LCD显示出亮度均匀的星点,星点发出的光线经过准直光学系统后形成平行光射出,实现对无穷远恒星的模拟显示。TFT-LCD显示器的星图显示由计算机控制,根据计算机输入的数据,对不同的星图进行模拟显示,从而实现对星敏感器星图识别和星跟踪等功能的检测。
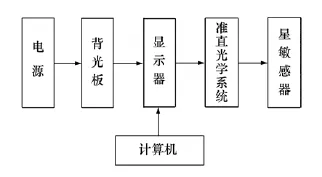
图1 动态星模拟器原理图Fig.1 Schematic diagram of dynamic star simulator
3 星点位置的测量
利用计算机控制TFT-LCD显示器,使其在整个视场中显示如图 2所示的网格(间距为126 pixel),网格中每一个交叉点代表一个待测的星点。以TFT-LCD显示器所使用的视场中心点O为中心,使用莱卡TM5100A经纬仪对各点相对于中心点的俯仰角和方位角进行测量。

图2 动态星模拟器测试网格Fig.2 Test grid of dynamic star simulator
4 星点坐标的修正
4.1 网格上各星点的位置计算
用经纬仪测量给定网格上各星点的方位角和俯仰角(αi,βi),中心星点 O 为(α0,β0),则网格上任意一星点P(mi,ni)相对中心O的方位角和俯仰角(α0i,β0i)为:

P点相对中心点O的实测像素数位置坐标(m′i,n′i)为:

式中,α,β为P点相对于中心点O的方位和俯仰角,f ′为光学系统焦距实测值,spix为像元尺寸。
4.2 修正系数计算
当被测点P相对于中心点O的方位角和俯仰角为(α0,β0)时,其对应的星点位置为(m′i,n′i),但实际应该点亮的像素理论位置为(mi,ni),即需要修正系数把(m′i,n′i)修正到(mi,ni)才能满足修正要求。任意被测星点P的横向修正系数km和纵向修正系数kn为:

为了确定网格点之外星点的修正系数,需要统计网格点上各星点的修正系数与对应星点位置的关系。通过观察它们在整幅星图中的分布规律,确定如何分区计算各点修正系数的均值。验证取均值后各点的修正系数是否满足修正要求,点P进行修正后的位置(m″i,n″i)为:

判断m′i,n″i和mi,ni的关系,如不满足要求则需要重新划分区域计算均值,直到满足要求为止。
4.3 曲线拟合
根据经纬仪对网格上各点的测量数据,对分区后各区域的修正系数进行处理。在一个被划分好的区域中,各点的修正系数k是其所在位置的函数,应用这些已知的函数对,以位置为(方位或俯仰)横坐标,系数为纵坐标,使用matlab软件进行最小二乘拟合,得到该区域的方位修正系数k和俯仰修正系数K关于星点坐标(x,y)的曲线方程,根据方程可求得分区内任意星点位置的修正系数。
(1)当x>0,y>0时
星点方位坐标x的修正系数拟合曲线如图3所示。

图3 方位坐标修正系数拟合曲线Fig.3 Fitting curve of correction factor for positon
方位坐标修正系数方程为:


图4 俯仰坐标修正系数拟合曲线Fig.4 Fitting curve of correction factor for pitch
星点俯仰坐标y的修正系数拟合曲线如图4所示。
俯仰坐标修正系数方程为:

同理可求出其它区域的方位、俯仰坐标的修正系数曲线方程。
(2)当x>0,y<0时
方位坐标修正系数方程为:

俯仰坐标修正系数方程为:

(3)当x<0,y>0时
方位坐标修正系数方程为:俯仰坐标修正系数方程为:


(4)当x<0,y<0时
方位坐标修正系数方程为:
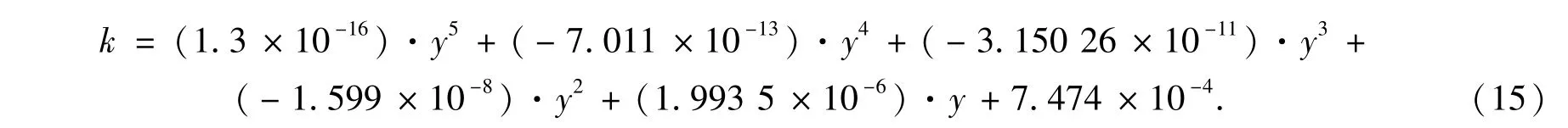
俯仰坐标修正系数方程为:
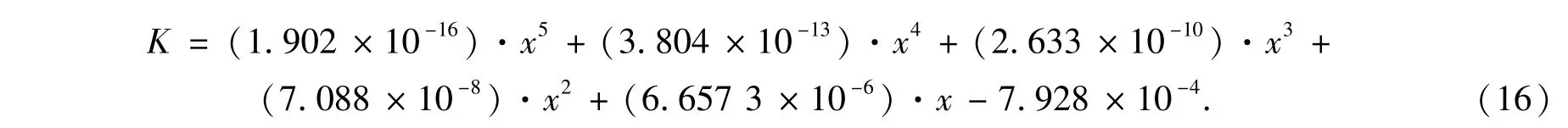
5 修正结果检验
5.1 星点位置误差的计算
若任意两个星点P1,P2在TFT-LCD显示器有效像面上用经纬仪测出方位角和俯仰角为 P1(u1,v1),P2(u2,v2),则星点P1,P2间的星对角距实测值θ0可由下式计算得到:

式中,δ1=90°-β1,δ2=90°-β2。
若任意两个星点P1,P2在TFT-LCD显示器有效像面上的理论位置为P1(u2,v1),P2(u2,v2),则星点P1,P2间的星对角距理论值θ0为:

式中,f为准直光学系统焦距的实测值。
任意两个星点的星对角距误差Δθ为:

取所有任意两点Δθ最大者为模拟器的星对角距误差。若选P1点为视场中心点O,则上式中Δθ为单星位置误差。
5.2 星点位置误差修正结果
根据修正系数的分区,将拟合好的修正系数曲线方程输入计算机,随机设置10个星点坐标,并通过计算机控制TFT-LCD显示输出。利用经纬仪对10个星点进行测量,并计算其相对于中心点O的星对角距误差(即星点位置误差),测量结果如表1所示。经过测量,10个点的星点位置误差均小于35″,满足动态星模拟器设计要求。

表1 修正后的星点位置误差Tab.1 Corrected star position errors
6 结 论
本文利用经纬仪对动态星模拟器显示的星点网格进行了测量。根据测量的数据,计算了各网格上各星点的位置误差及修正系数。利用Matlab软件对分区处理的修正系数进行了曲线拟合,并得出了修正系数的方程。通过经纬仪重新测量,证明修正后动态星模拟器显示的星点位置误差均小于35″,达到了动态星模拟器的设计要求。
[1]刘亚平,李娟,张宏.星模拟器的设计与标定[J].红外与激光工程,2006,35(增1):331-334.LIU Y P,LI J,ZHANG H.Design and calibration of star simulator[J].Infrared and Laser Eng.,2006,35(s1):331-334.(in Chinese)
[2]赵晨光,谭久彬,刘俭,等.用于天文导航设备检测的星模拟装置[J].光学精密工程,2010,18(6):1326-1332.ZHAO CH G,TAN J B,LIU J,et al..Star simulator for testing celestial navigation equipment[J].Opt.Precision Eng.,2010,18(6):1326-1332.(in Chinese)
[3]张文明,林玲,郝永杰,等.小型星模拟器中星图动态显示系统的设计[J].光电工程,2000,27(5):11-14.ZHANG W M,LIN L,HAO Y J,et al..Design of a dynamic display system for star map in small-sized star simuator[J].Opto.Elect ronic Eng.,2000,27(5):11-14.(in Chinese)
[4]巩岩,胡宜宁,赵阳.基于数字光处理技术的小型星模拟器设计[J].光学精密工程,2007,15(11):1698-1704.GONG Y,HU Y N,ZHAO Y,et al..Design of a mini star simulator based on digital optical processing[J].Opt.Precision Eng.,2007,15(11):1698-1704.(in Chinese)
[5]蒋汉元,李雪雷,陈涛,等.光电经纬仪图像测量中的自动调焦系统研究[J].计算机测量与控制,2010,18(1):183-185.JIANG H Y,LI X L,CH T,et al..Research on automatic focusing system for theodolite′s image measurement[J].Computer Measurement&Control,2010,18(1):183-185.(in Chinese)
[6]李春艳,李怀锋,孙才红.高精度星敏感器天文标定方法及观测分析[J].光学精密工程,2006,14(4):558-563.LI CH Y,LI H F,SUN C H.A stronomical calibration method and observation analysis for high-accuracy star sensor[J].Opt.Precision Eng.,2006,14(4):558-563.(in Chinese)
[7]段晓东.全天球实时星光模拟器的设计与标定[J].控制工程,1997(2):23-33.DUAN X D.Design of real-tiem star simulator in whole celestial sphere[J].Controlling Eng.,1997(2):23-33.(in Chinese)
[8]刑飞 ,武延鹏 ,董瑛,等.微型星敏感器实验室测试系统研究[J].光学技术,2004,30(6):703-709.XING F,WU Y P,DONG Y,et al..Research of laboratory test system for micro-star tracker[J].Opt Tech.,2004,30(6):703-709(in Chinese)
[9]唐建国,袁家虎,吴钦章.液晶光阀星图模拟设计与实现[J].光电工程,1999,26(增):75-78.TANG J G,YUAN J H,WU Q ZH.Design and implementation of star pattern simulation with liquid crystalight valve[J].Opto-Electronic Eng.,1999,26(s):75-78.(in Chinese)
Abstract:To measure total solar irradiance accurately,the solar irradiance absolute radiometer SIAR-3a with the ability of automatic solar tracking is designed and constructed.The principle and structure of the solar irradiance absolute radiometer SIAR-3a are presented in this paper and its control scheme for automatic double-axis solar tracking is proposed.The solar irradiance absolute radiometer SIAR-3a imposes electricity to calibrate the total solar irradiance,which is able to measure the total solar irradiance and follow the sun simultaneously.In the calibration experiments,the corresponding rms error limit of SIAR-3a amounts to 0.06%at the 3σ level,which has been calibrated to World Radiometric Reference stored in World Radiation Centre(WRC)in Davos,Switzerland.The experiment results indicate that SIAR-3a works reliably and accurately.
Key words:solar irradiance;total solar irradiance;absolute radiometer;solar tracking;irradiation calibration
文章编号1674-2915(2011)03-0252-07
王 俣1,张国玉1,2,高玉军3,孙高飞1,郑 茹1
(1.长春理工大学,吉林长春130022;
2.光电测控与光信息传输技术教育部重点实验室,吉林长春130022;
3.中国科学院长春光学精密机械与物理研究所,吉林长春130033)
Star position correction of dynamic star simulator based on TFT-LCD
WANG Yu1,ZHANG Guo-yu1,2,GAO Yu-jun3,SUN Gao-fei1,ZHENG Ru1
(1.Changchun University of Science and Technology,Changchun 130022,China;2.Key Laboratory of Optoelectronic Measuring-controlling and Optical Information Transmiting Technology,Ministry of Education,Changchun 130022,China;3.Changchun Institute of Optics,Fine Mechanics and Physics,Chinese Academy of Sciences,Changchun 130033,China)
This paper describes the working principle of the dynamic star simulator based on a TFT-LCD and the calculation of the revised star angular distance error.A theodolite is used to measure the star point on the grid shown by the dynamic star simulator,then the position error correction factor of each star point is calculated based on the measured data.The correction coefficient of the star point on the grid is partitioned,and Matlab software is used for the curve fitting of each partition′s revised correction coefficients to get the(azimuth or elevation)coordinate equations of the star position.The experimental result shows that the revised star angular distance error is less than 35″,which meets the design requirements of the dynamic star simulator.
dynamic star simulator;theodolite;curve fitting
Solar irradiance absolute radiometer with ability of automatic solar tracking
WANG Hong-rui,FANG Wei
(Changchun Institute of Optics,Fine Mechanics and Physics,Chinese Academy of Sciences,Changchun 130033,China)
V448
A
1674-2915(2011)03-0247-05
2011-01-14;
2011-04-13
王 俣(1984—),男,吉林长春人,硕士研究生,主要从事精密测控技术与仪器方面的研究。
E-mail:richie_wang@126.com
张国玉(1962—),男,吉林松原人,博士,研究员,博士生导师,主要从事空间科学与技术、光电仪器与探测技术方面的研究。E-mail:zh_guoyu@yahoo.com.cn

