带参数扰动非线性系统的变结构控制
刘 凯,董西广
(河南工程学院 数理科学系,河南 郑州 451191)
变结构控制是系统控制的一种重要方法,它在20世纪60年代就已经受到了广泛的关注,在鲁棒控制、自适应控制、状态观测等方面都有广泛的应用[1-2].它的中心思想是在控制系统中设计切换面和一个关于切换面的切换控制律,使得系统轨迹最终可以达到切换面[3].这项技术为实现系统的一些目标提供了一个设计控制面的基本框架.
对于线性系统,文献[4]解决了不需要经典形式的Ricatti方程的求解问题,通过此形式,使得系统轨迹最终达到切换面的Lyapunov函数和控制律很快被设计出来,但是这些考虑都是在线性系统中.文献[5]给出了不确定线性系统的变结构控制问题,但是系统考虑的只有状态参数的扰动问题,不包含控制参数的扰动.文献[6]将之前的滑动面改进为状态空间中的一个子集滑动区域,在滑动区域内,0控制使得Lyapunov函数单调递减,之后,在滑动区域外设计了一个控制使得系统状态最终进入滑动区域,从而使系统全局渐近稳定.
另外,文献[7]考虑了一个非线性时变系统的变结构控制,通过微分Ricatti方程的解设计出系统的滑动区域,同时给出了一个变结构控制律使得系统最终进入滑动区域,而系统Lyapunov函数在滑动区域内单调递减.但是,文献[7]同样只考虑了系统的状态扰动,并未考虑系统的控制参数扰动.
本文考虑了一个非线性时变带参数扰动的变结构控制问题,此非线性系统可以由一个状态决定的线性时变系统来描述,同时假定系统满足若干假设.在此假设之下,给出了一个状态决定的微分Ricatti方程,并通过此Ricatti方程的解设计出滑动区域.之后,给出变结构控制律.此变结构控制律使得系统最终从滑动区域外进入滑动区域内,而在滑动区域内,系统Lyapunov函数单调递减,从而使得系统渐近稳定.
本文的第1部分描述问题,并且给出一些定义以及前人给出的定理;第2部分为系统的主要结果;最后,给出问题的研究方向.
1 问题描述
考虑如下一个带参数扰动的单输入非线性时变系统:
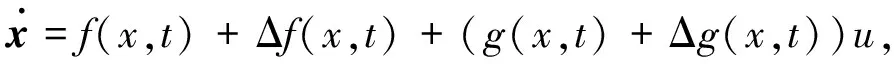
(1)
其中,x∈Rn为系统状态,u∈R为系统的单输入变量,且对于x∈Rn,t∈R+总有f(x,t),g(x,t)∈Ck,g(x,t)≠0,Δf(x,t)和Δg(x,t)为系统中的参数扰动,同时,对于f(x,t),Δf(x,t),g(x,t)和Δg(x,t)都有适当的维数.
假设对于∀t∈R+,有f(0,t)=0.f(x,t)关于x连续可微且关于x满足局部李普希兹条件,则对于非线性系统(1)的稳定性可以等价为如下形式的状态决定线性时变系统[8]:

(2)
其中,A(x,t)x=f(x,t),ΔA(x,t)x=Δf(x,t),ΔA(x,t)=E1(x,t)Δ1(x,t)F1(x,t),B(x,t)=g(x,t),ΔB(x,t)=Δg(x,t),ΔB(x,t)=E2(x,t)Δ2(x,t)F2(x,t),对于i=1,2时,A(x,t),B(x,t)以及Ei(x,t),Fi(x,t)为适当维数的确定系统矩阵,而Δi(x,t)为满足适当维数的不确定矩阵.
在文献[5-7]中,带参数扰动的系统并没有给出适当的考虑,为了给出这类系统的稳定性控制,首先给出如下几个假设.
假设1 对于不确定矩阵Δ(x,t)=diag(Δ1(x,t),Δ2(x,t)),满足:
ΔT(x,t)Δ(x,t)≤I.
假设2 存在常数0<λ<1,使得对于x∈Rn,t∈R+,有
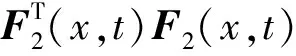
本文将要给出基于滑动区域的控制律设计方法,在由此设计出的控制律之下,闭环系统全局渐近稳定.为了给出这样的控制律,我们首先给出滑动区域的定义以及一个重要引理.
1.1 非线性时变滑动区域
对于线性时不变系统,文献[5]给出了一个线性时不变滑动区域,在此滑动区域内,Lyapunov函数递减.与这种情况类似,对于非线性时变系统(2),我们可以设计如下定义的非线性时变滑动区域.
定义1 如下式定义的状态空间Rn的子集:
S(t)={x|s2(x,t)≤δ2(x,t),x∈Rn,t∈R+},
(3)
称为非线性时变滑动区域,若满足如下条件:
(1)对于Lyapunov函数V(t)=xTP(x,t)x,∀x∈Rn(x≠0),t∈R+,有V(t)>0;
(2)存在一变结构控制律,在控制律下,Lyapunov函数沿系统(2)轨迹的微分满足

(4)
其中,P(x,t)∈Rn×n为对称正定矩阵函数,R(x,t)∈Rn×n为对称半正定矩阵函数,$R(x,t)=CT(x,t)C(x,t),C(x,t)∈Rl×n,(A(x,t),C(x,t))对于任意的x∈Rn,t∈R+可观测,且切换函数s(x,t)和状态决定时变二次函数δ2(x,t)的平方根δ(x,t)由(5)式和(6)式描述:
s(x,t)=S(x,t)x,S(x,t)∈Rl×n,
(5)

(6)
本文将要给出基于系统(2)的滑动区域及相对于滑动区域的滑动控制律,并证明在此滑动控制律控制之下,Lyapunov函数递减,从而使得系统渐近稳定.
1.2 相关引理
在本节中,将要用到一些引理,这些引理对于本文结论的证明非常重要.
引理1[13-14]对于单输入时变非线性系统(2),任意给定的对称正定矩阵函数Q(x,t),若(A(x,t),B(x,t))能控,则存在对称正定矩阵函数P(x,t),满足如下的状态决定微分Riccati方程:
(7)
初始条件为P(x(t0),t0)=P0>0.
此引理在文献[13-14]中给出了证明,文献[7]的结论主要是基于此引理所给出的.文献[7]首先基于引理中Riccati方程的解给出了滑动区域,同时也给出了如下的非线性时变控制律:
u=-BT(x,t)P(x,t)x,
(8)
并且在此控制律之下,证明了系统的Lyapunov函数单调递减.


(9)
对于任意的x∈Rn,t∈R+,ΔA(x,t)=ΔB(x,t)=0则在控制律(8)控制之下,系统(2)全局渐近稳定.
2 主要结论
本节将要给出本文的主要结论.对于带参数扰动的状态决定线性时变系统(2),可以将之化为如下形式的系统:
(10)
其中,E(x,t)=(E1(x,t),E2(x,t)).此形式相对于系统(2),将不确定条件完全孤立了出来.


(11)
初始条件为P(x(t0),t0)=P0>0.
下面,我们分两步来考虑控制律的设计问题,首先在滑动区域中设计出使得Lyapunov函数递减的控制律.
定理1 对于满足假设1,2,3的系统(10),如果:
(1)对于对称正定矩阵Q(x,t)∈Rn×n,正定矩阵函数P(x,t)是微分Riccati方程(11)的解,且Lyapunov函数由P(x,t)构造得到;
则非线性时变滑动区域可以定义为:
S(t)={x|s2(x,t)≤δ2(x,t),x∈Rn,t∈R+},
(12)
其中,δ(x,t)和切换函数s(x,t)为如下形式:
(13)
在此控制律下,在滑动区域中,Lyapunov函数沿着闭环系统轨迹单调递减.
证明对于Lyapunov函数V(t)=xTP(x,t)x,考虑其沿着系统轨迹的导数,有:

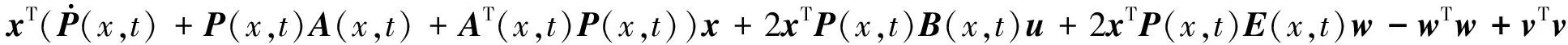
代入控制律u,又因为在滑动区域中,且λ∈(0,1),因此有:
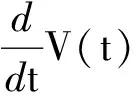
结论得证.
由如上定理1可以得到,在(13)的控制之下,Lyapunov函数沿着闭环系统(10)在滑动区域内的系统轨迹单调递减.因此,我们只需要在滑动区域之外重新设计一个控制律,此控制律可以将滑动区域之外的系统轨迹拉回到滑动区域内,从而保证系统的全局稳定性.
定理2 对于满足假设1,2,3的系统(10),如果
(1)α(x,t),β(x,t)为如下定义的标量函数:
(14)
(15)
(2)存在常数0<γ<1,使得F2(x,t)=γB(x,t);
(3)非线性时变滑动区域和非线性时变切换函数s(x,t)的形式由定理1给出,基于滑动区域给出的滑动控制律定义如下:
(16)
则在非线性滑动控制律(16)下,系统(10)全局渐近稳定.
定理2的证明和定理1的证明过程基本类似,在这里不再给出.
参考文献:
[1] Edwards C, Spurgeon S K. Sliding Mode Control Theory and Applications[M]. London:Taylor & Francis, 1998.
[2] Utkin V I. Variable structure systems with sliding modes[J]. IEEE Trans Automat Cont, 1977(22):212-222.
[3] Utkin U. Sliding Models in Control and Optimization[M]. London: Springer-Verlag, 1992.
[4] Su W C, Drakunov S V, Ozguner U. Constructing discontinuity surface for variable structure systems[J]. Automatica, 1996,32(6):925-928.
[5] Ferrara A. A variable structure convex programming based control approach for a class of uncertain linear systems[J].System & Control Letter, 2005(54):529-538.
[6] Furuta K, Pan Yaodong. Kariable structure control with sliding sector[J]. Autormatica, 2000(36):211-228.
[7] Pan Y, Krishna D K, Liu G. Design of variable structure control system with nonlinear time-Varying sliding sector[J]. IEEE Trans on Automatic Control, 2009,54(8): 1981-1986.
[8] Cloutier J. State-dependent Riccati Equation Techniques: an Overview[C]. Proc Amer Control Conf Albuquerque NM, 1997:932-936.
[9] Anderson B,Moore J. Optimal Control-Linear Quadratic Methods[M]. NJ: Prentics Hall, 1990.
[10] Kokotovic P,Areak M. Conctructive nonliear control: a historical perspective[J]. Automatica, 2001,37(5):637-662.
[11] Bartolini G, Ferrara A,Usai E. Chattering avoidance by second order sliding mode control[J]. IEEE Trans Autom Control, 1998(43):241.
[12] Sontag E D, Wang Y. On characterizations of the input-to-state stability property[J]. Systems & Control Letter, 1995(24):351-359.
[13] Sontag E D, Wang Y. A smooth converse Lyapunov theorem for robust stability[J]. Control & Optimization, 1996(13):124-160.
[14] Kachroo P, Tomizuka M. Hattering reduction and error convergence in the sliding-mode control of a class of nonlinear systems[J]. IEEE Transactions on Automatic Control, 1996(41):1063-1068.
[15] Sun X, Zhao J, Hill D J. Stability and L∞-gain analysis for switched delay systems: a delay-dependent method[J]. Automatica, 2006(42):1769-1774.
[16] Liberzon D. Switching System and Control[M]. Boson:Birkhauser,2003.

