一类递推数列中的平方数

管 训 贵

(泰州师范高等专科学校 数理系，江苏 泰州 225300)

一类递推数列中的平方数

管 训 贵

(泰州师范高等专科学校 数理系，江苏 泰州 225300)

设{xn}是满足递推关系x0=1，x1=a＞1，xn+2= 2axn+1−xn的数列.本文给出了：a=5，9，169以及 9 801时所有可使xn是平方数的正整数n.

递推数列；平方数；Diophantine方程；Pell方程；正整数解；存在性

1 引言及主要结论

解Diophantine方程的方法很多，其中有一种方法叫递推数列法，它是先将Diophantine方程化为递推数列(如果可能的话)，然后通过讨论递推数列的数论性质，再利用各种手段制造矛盾以求得所给方程解的方法.一方面，某些Diophantine方程可以化为递推数列来解；另一方面，Diophantine方程的解也可以用来研究递推数列.比如，Diophantine方程421x−Dy= 的结果可在递推数列

中得到应用.设a2−1=Db2，D＞0无平方因数，则(1)的正整数解是

借助上述结论，本文证明了如下：

定理设{xn}是满足递推关系x0=1，x1=a＞1，xn+2= 2axn+1−xn的数列，则当a=5时，xn是平方数当且仅当n=0, 2；当a=9时，xn是平方数当且仅当n=0, 1；当a=169时，xn是平方数当且仅当n=0, 1, 2；当a= 980 1时，xn是平方数当且仅当n=0, 1.

2 关键性引理

引理1Diophantine方程x4− 6y2= 1仅有正整数解(x,y) = (7, 20).证明可参见文献[1] .

引理3Diophantine方程x2− 2y4=−1仅有正整数解(x,y) = (1, 1)，(239, 13).证明可参见文献[2] .

引理4Diophantine方程

仅有正整数解(x,y) = (3, 4).

证明设(x,y)是方程(2)的正整数解.若2∣x，则 gcd(x2− 1,x2+ 1)= 1，故(2)给出

这里 (y1,y2)= 1.

但由引理2知，(5)无正整数解，故(4)给出

再由(6)的前两式得出x2= 5y12+y22.

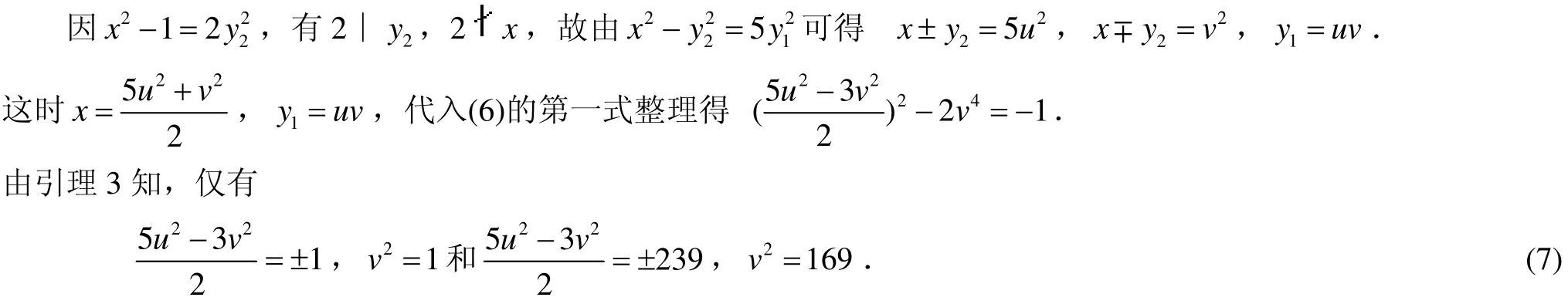
解(7)得u2=v2=1，于是x=3，y=4.引理4得证.

用类似于引理4的证明方法可证下述

引理5Diophantine方程x4− 29y2=1仅有正整数解(x,y) = (99, 1 820).

引理6Diophantine方程x4−Dy2= 1，D＞0且不是平方数，最多有两组正整数解(x,y).证明可参见文献[3] .

引理7Diophantine方程x4− 1 785y2= 1仅有正整数解(x,y) = (13, 4),(239, 1 352).

证明因 134−1 785· 42=1，2394− 1 785· 1 3 522=1，故由引理6知，引理7得证.

3 定理的证明

1) 因Diophantine方程x2− 6y2= 1的基本解是(x,y) = (5, 2)，对应的递推数列为xn+2= 10xn+1−xn，x0=1，x1=5，故由引理1知，a=5时，除开x0=1，x2=49外，无其它的平方数.

2) 因Diophantine方程x2− 5y2= 1的基本解是(x,y) = (9, 4)，对应的递推数列为xn+2= 18xn+1−xn，x0=1，x1=9，故由引理4知，a=9时，除开x0=1，x1=9外，无其它的平方数.

3) 因Diophantine方程x2− 1 785y2= 1的基本解是(x,y) = (169, 4)，对应的递推数列为xn+2= 338xn+1−xn，x0=1，x1=169，故由引理7知，a=169时，除开x0=1，x1=169，x2= 57 121外，无其它的平方数.

4) 因Diophantine方程x2− 29y2= 1的基本解是(x,y) = (9 801, 1 820)，对应的递推数列为xn+2=19 602xn+1−xn，x0=1，x1= 9 801，故由引理5知，a= 9 801时，除开x0=1，x1= 9 801，外，无其它的平方数.

综上，定理得证.

[1] 曹珍富.丢番图方程引论[M].哈尔滨:哈尔滨工业大学出版社,1989:49-51,172-173.

[2] LJUNGGREN W. Zur Theorieder Gleichungx2+1=Dy4[J].Avh.Norske Vid. Akad.Oslo,1942,1(5):1-126.

[3] LJUNGGREN W. Über die Gleichungx4−Dy4= 1[J].Arch.Math.Naturvid.,1942,45(5):61-70.

The Primes in a Family of Recurrence Sequences

GUAN Xun-gui
(Department of Mathematics＆Physics, Taizhou Normal College, Taizhou, Jiangsu 225300, China)

Let{xn}be a sequence which satisfyx0=1，x1=a＞1，xn+2= 2axn+1−xn. In this paper, all positive integersnthat make the formxnto be squares were given whena=5, 9, 169 and 9 801.

recurrence sequence; square; Diophantine equation; Pell’s equation; positive integer solution; existence

O156

A

1673-2065(2011)04-0004-02

2011-04-18

泰州师范高等专科学校重点课题资助项目(2010-ASL-09)

管训贵(1963-),男,江苏兴化人,泰州师范高等专科学校数理系副教授.

(责任编校：李建明英文校对：李玉玲)