黎曼流形上的Ricci曲率张量及其应用

焦慧平，肖德华

(1.中州大学 信息工程学院，郑州 450044；2.信阳农业高等专科学校 计算机科学系，河南 信阳 464000)

引言

令M是一个紧致连通的n维黎曼流形，文献[1]给出了Schouten张量[2]在局部共形对称与局部共形平坦黎曼流形上的应用，在此通过对Ricci曲率张量的研究得到以下结论:

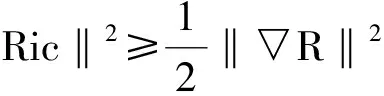
推论1 M是一个紧致连通的具常数量曲率的黎曼流形，Rij,k=Rik,j，如果M的截面曲率为正，则M是一个Einstein空间。

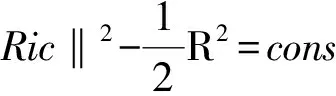
1.预备知识

设M是n维紧致定向连通光滑黎曼流形，(e1,e2,…,en)为M上的局部标架场，{ω1,ω2,…,ωn}为其对偶余标架场，M的结构方程：

dω1=ωjΛωji,ωij+ωji=0,

其中ωij是M的Levi-Civita联络，Rijkl是M的黎曼曲率，且Rijkl有不可约分解

(1)

其中Wijld，Rij和R分别表示Wey1共形曲率张量的分量，Ricci曲率张量Ric的分量和数量曲率。

M的Ricci曲率张量Ric的分量Rij和数量曲率R分别由下式定义

Rij∑Rikjk，R=∑Rkk

记Δ和▽分别表示M上Levi-Civita 联络的协变微分算子和Laplace算子，并将协变导数的局部表示记为

Rij,k=▽ekRij,Rij,ld=▽el▽ekRij,

ΔRij=∑Rij,kk等。

一阶协变导数例如Rij,k和二阶协变导数例如Rij,ld定义为

Rij,kωk=dRij+Rilωlg+Rjkωki,

Rij,ldωl=dRij,k+Rlj,kωli+Ril,kωlj+Rij,lωlk。

并且Ricci恒等式可类似如下定义

Rij,ld-Rij,lk=RimRmjkl+RjmRmikl。

经计算得

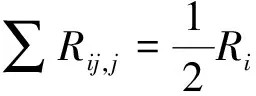
(2)

(3)

2.主要结论的证明

首先引进一个如下定义的▯算子：

其中f∈C2(M,R)，根据文献[3]，可以验证▯是关于M的L2-内积自伴的，即∫Mnf▯g=∫Mng▯f。

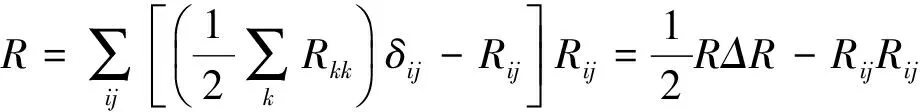
(4)

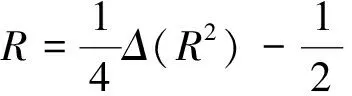
(5)

证明：由(3)式得

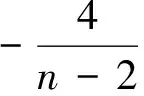
再由已知条件知结论成立。

利用Ricci恒等式及Rij,k=Rik,j得

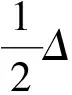
=‖▽Ric‖2+∑Rij[(Rij,kk-Rik,jk)+(Rik,jk-Rik,lg)+(Rik,lj-Rkk,ij)+Rkk,ij]

=‖▽Ric‖2+∑RijRij+∑Rij(RilRlkjk+RlkRlijk)

(6)

将(6)式代入到(5)式得

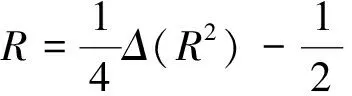
在p∈M点附近选取标准正交标架场e1,e2,…,en，使得Rij=λiδij，则

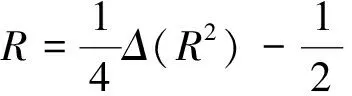
由于M是紧致的，并且Δ和▯是自伴的，对上式积分得

(7)

根据引理1知，推论1，2显然成立。

根据引理2知，推论3成立。

[1]纪楠，郭震．具有调和共形曲率的黎曼流形上的Schouten张量及其应用[J]．云南师范大学学报：自然科学版，2005，25(2)：1-4．

[2]Hu Zejun，L i Haizhong ，Simon U．Schouten curvature functions on locally conformally flat Riemannian manifolds[J]．J．Geom．，2008(88)：75-100．

[3]Cheng S Y，Yau S T．Hypersurfaces with constant scalar curvature[J]．Math．Ann．，1977(225)：195-204．

[4]罗明珍，郭震.局部共形的黎曼流形上的Schouten张量[J].云南师范大学学报:自然科学版,2011,31(4):58-61.