粗糙模糊子格＊

郝 景，李庆国

（湖南大学数学与计量经济学院，湖南长沙 410082）

Pawlak提出粗糙集是为了处理不确定信息和不明确信息.粗糙集理论作为一种信息处理的工具，近年来飞速发展，并广泛应用于数据挖掘、智能模式识别、图像处理等领域.

近似空间在粗糙集理论中有极其重要的地位，其发展主要分布在以下几个方面.第一，等价关系的一般化.Pawlak提出的粗糙集是基于等价关系，随着该理论的应用研究，把等价关系推广到一般关系上，以解决更一般的问题，从而提出了广义粗糙集.第二，粗糙集的模糊化.模糊粗糙集最早由D.Dubois等［1］提出.此后，出现了各种各样的模糊粗糙集.第三，粗糙代数结构的研究.如Biswas等［2］.提出了粗糙群、粗糙子群的概念并且详细讨论了其性质.随后，一些学者详细讨论了粗糙环、粗糙模等.Estaji等［3］研究了粗糙模糊子格，但他们讨论的是基于格上经典的同余关系的粗糙模糊子格.

在本文中，我们提出了格上的模糊同余关系，并基于该模糊同余关系，研究了粗糙模糊子格的一些性质.最后，我们提出了模糊关系同态，讨论了模糊关系同态所定义的模糊同余关系，并得到了如下结论：这类同态保持粗糙上逼近.

1 预备知识

在本文中，我们用完备剩余格作为真值结构.剩余格（L，⊗，→，∨，∧，0，1）满足：（L，∨，∧，0，1）是有界格，0，1分别是其最大最小元；（L，⊗，1）是一个可换的幺半群；（⊗，→）是一个伴随对，也就是说x⊗y≤z当且仅当x≤y→z.

下面我们重新回顾一下剩余格的一些基本性质，请参考［4－5］.⊗关于左右两项是单调增的，→关于第一项是单调减，关于第二项是单调增.剩余格L上的预补运算如下定义：⇁：L→L，⇁a＝a→0.对于所有的x，y∈L，｛xi｝⊆L，下面的性质成立：

给定一个集合X，它的L模糊子集A是从X到L的映射，参见文献［6］.对于任意的A，B，∈LX，新的模糊集可构造如下：

L模糊关系R是从X×X到L的映射.称R是自反的，如果R（x，x）＝1，∀x∈X；R是对称的，如果R（x，y）＝R（y，x），∀x，y∈X；R是传递的，如果R（x，y）⊗R（y，z）≤R（x，z），∀x，y，z∈X.若R是自反，对称，传递，则称R是L模糊等价关系.

（X，R）是L模糊近似空间，其中X非空，R是X上的L模糊关系.对于任意的A∈LX，x，y∈X，上下逼近算子定义如下：

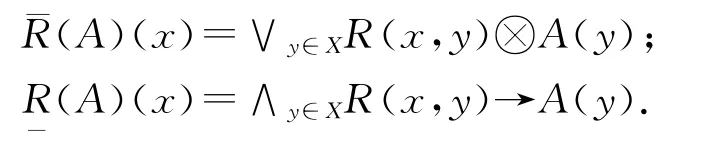
L模糊近似空间的具体性质请参考文献［7］.

2 粗糙模糊子格

在本文中，我们总是假定L是一个完备剩余格.下面的定义参考文献［8－9］，是文献中的推广.

定义1 假定（X，∨，∧）是格.A∈LX，如果对x，y∈X，A（x）⊗A（y）≤A（x∨y）∧A（x∧y）.那么称A为X的模糊子格.

定义2 假定（X，∨，∧）是格，A∈LX.

1）如果A（x）⊗A（y）＝A（x∧y）对任意的x，y∈X成立，则称A是一个模糊滤子；

2）如果A（x）⊗A（y）＝A（x∨y）对任意的x，y∈X成立，则称A是一个模糊理想.

定义3 给定（X，∨，∧）是格，R∈LX×X且R是模糊等价关系.对任意的xi，yi∈Z，i＝1，2，如果

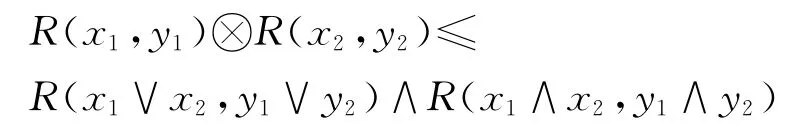
成立，那么我们称R是模糊同余关系；

如果

成立，那么我们称R是强模糊同余关系.

命题1 给定（X，∨，∧）是格，A∈LX且A是模糊理想，Z⊆X.那么

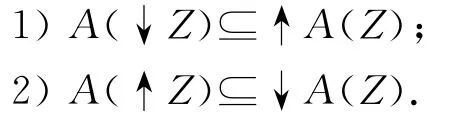
证明：对于任意的x∈↓Z，存在z∈Z使得x≤z，那么由于A是模糊理想，我们有A（x）⊗A（z）＝A（x∨z）＝A（z），从而A（x）≥A（z）.

同样可以证明第二个式子.

定理1 给定（X，∨，∧）是格，A∈LX.

证明：1）对于∀x，y∈X，

因R是模糊同余关系，所以第一个不等式成立.同样，可以有¯R（A）（x）⊗¯R（A）（y）≤¯R（A）（x∧y）.已证.

2）因为R是强模糊同余关系，所以对于任意x1，x2，y1，y2∈X，有

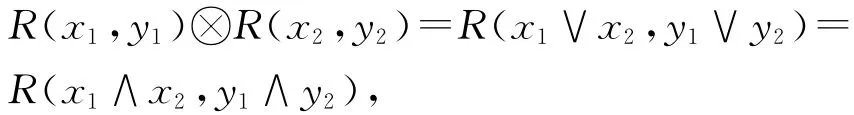
从而对任意x，y∈X，有

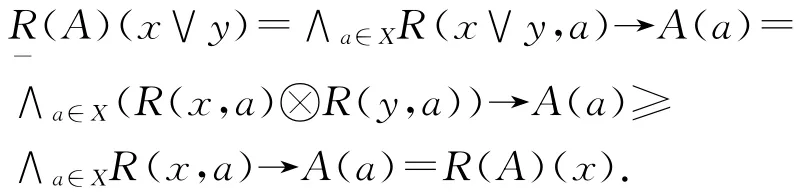
定理2 给定（X，∨，∧）是格，A∈LX.R是X上的强模糊同余关系，则有下面关系成立：

证明：同定理1中1）的证明.

定理3 给定（X，∨，∧）是格，A∈LX.R是X上的强模糊同余关系，则有下面关系成立：

证明：同定理1中2）的证明.

引理1 假定X是任意的集合，R1，R2是X上的模糊等价关系.那么R2是等价关系当且仅当R2＝R1.

证明：自反性和对称性显然成立.下面仅证传递性.对所有的x，y，z∈X，有

注：由引理1，我们容易得出，R1，R2是格X上的模糊同余关系.R2是模糊同余关系当且仅当R1o R2＝R1.

定理4 给定（X，∨，∧）是格，A∈LX.R2是模糊同余关系且R2＝R1，那么

定义4 给定X，Y是格，f∈LX×Y.如果f满足：任意x1，x2，y1，y2∈X，

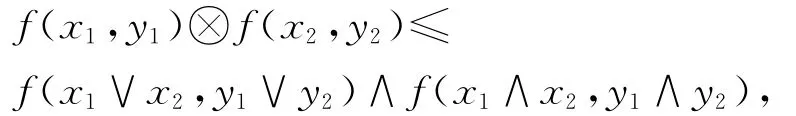
那么称f为模糊关系同态.

注：X，Y如定义4给定.

1）对于A∈LX，B∈LY，分别可以定义f（A）∈LY，f－1（B）∈LX如下，

2）我们可以分别定义X，Y上的等价关系如下：

［9］，容易得出，分别是X，Y的等价关系.若X，Y是格，则，分别是X，Y上模糊同余关系.

定理5 给定X，Y是格，f是模糊关系同态，A∈LX，那么f（（A））＝f（A）.

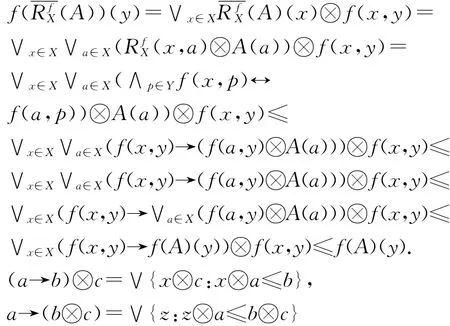
证明：对于y∈X，从而（a→b）⊗c≤a→（b⊗c），所以第一个不等式成立.已证.

定理6 给定X，Y是格，f是模糊关系同态，A∈LX.那么

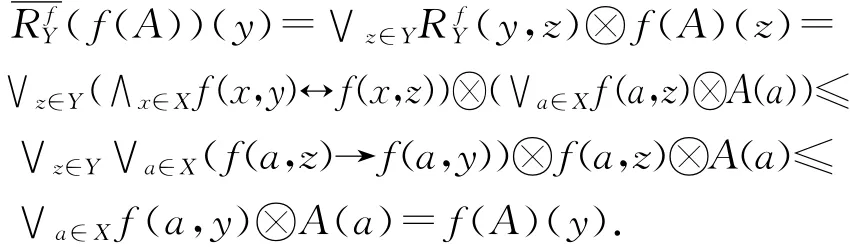
3 结 论

在本文中，我们讨论了粗糙模糊子格、粗糙模糊理想、滤子的一些性质.并且讨论了两个格在模糊同态关系下，模糊粗糙集的性质.

参考文献

［1］ DUBOIS D，PRADE H.Rough fuzzy sets and fuzzy rough sets［J］.International Journal of General Systems，1990，17：191－208.

［2］ BISWAS R，NANDA S.Rough groups and rough subgroups［J］.Bulletin of the Polish Academy of Sciences，1994，42：251－254.

［3］ ESTAJI A A，KHODAII S，BAHRAMI S.On rough set and fuzzy sublattice［J］.Information Sciences，2011，181（18）：3981－3994.

［4］ BLOUNT K，TSINAKIS C.The structure of residuated lattices［J］.International Journal of Algebra and Computation，2003，13（4）：437－461.

［5］ WARD M，DILWORTH R P.Residuated lattices［J］.Transactions of the American Mathematical Society，1939，45：335－354.

［6］ GOGUEN J A.L－fuzzy sets［J］.Journal of Mathematical Analysis and Applications，1967，18：145－174.

［7］ SHE Y，WANG G.An axiomatic approach of fuzzy rough sets based on residuated lattices［J］.Computers and Mathematics with Applications，2009，58：189－201.

［8］ ATTALLAH M.Completely fuzzy prime ideals of distributive lattices［J］.The Journal of Fuzzy Mathematics，2000，8（1）：151－156.

［9］ IGNJATOVIC J，CIRIC M，BOGDANOVIC S.Fuzzy homomorphisms of algebras［J］.Fuzzy Sets and Systems，2009，160：2345－2365.