次同步谐振中的非线性振荡分析
刘铁军,邓 斌
(1.中国能源建设集团黑龙江省电力勘察设计研究院,黑龙江哈尔滨150078;2.天津电力公司调度通信中心,天津300010)
0 引言
发生在带有串补电容系统中的次同步谐振是一种对发电机轴系造成巨大损坏的现象。其起因是汽轮发电机的轴系存在显著弹性,再加上机械与电气间的相互激励产生的频率低于同步频率的自发振荡。次同步谐振轻则使发电机大轴疲劳、产生裂纹,重则使其断裂。20世纪70年代,美国内华达州南部Mohave电站就由于次同步谐振引起了发电机大轴的两次扭振破坏[1],随后国内外电厂都出现过由于次同步谐振造成的发电机轴系损坏事件。
通常分析这种谐振采用小干扰稳定分析中的线性化分析方法,理论成熟、分析简单[1-2]。只要系统特征根中出现对应于次同步振荡频率的正复根,则表明系统将发生次同步谐振;若系统所有特征根都有负的实部,则系统是稳定安全的。但若对应于次同步频率的特征根出现在非双曲平衡点的邻域内,上述分析方法将不适用,因为此时发生的振荡属于非线性振荡范畴。由于系统本身非线性的作用,有可能使通常小干扰稳定分析认为稳定的系统跃变为轨道不稳定的,也就是由衰减振荡跃变为增幅振荡,不该出现的次同步谐振发生。同样,由于系统非线性的存在,也有可能使通常小干扰稳定分析认为不稳定的系统跃变为轨道稳定的,即小模等幅振荡的情况,这将极大地缓解次同步谐振的危害。美国西北部电力系统发生的一次次同步谐振就是这种类型的振荡[3]。因此,本文利用中心流形理论与分岐理论分析了发生在次同步谐振中的非线性振荡,利用数值微分算法分析了系统参数对这种非线性振荡性质的影响,最后通过数值仿真验证了新观点的正确性。
1 数学模型
分析次同步谐振用的数学模型为

式中:x为系统n维状态变量;α为能引起非线性振荡的系统参数,称之为分歧参数,分析用系统如图1所示。

图1 分析用系统图
与通常稳定分析所用数学模型不同,这里必须要考虑网络的暂态过程。把发电机轴系分为5个质量块:高压缸、中压缸、低压缸、发电机、励磁机,则各转子运动方程为
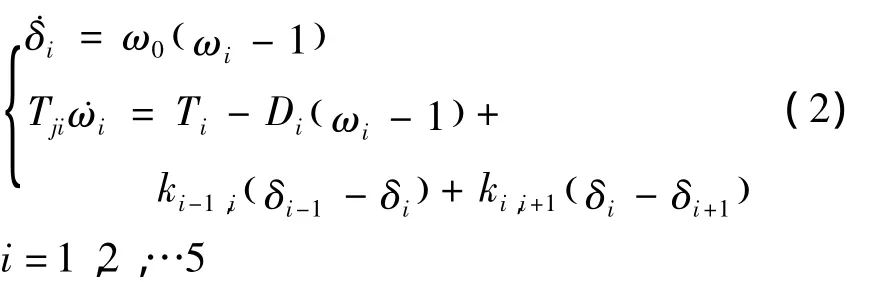
忽略发电机励磁调节器及阻尼绕组的作用,全系统状态方程及式(2)各参数意义及单位见文献[3]。
式(1)线性化后的系统为

式中:ΔΧ为非双曲平衡点x*处状态变量的增量,系统的雅可比矩阵。若λ是A阵n个i特征根中的第i个特征根,而且Re(λi)<0,i=1,2,…,n,则系统在小干扰下是渐近稳定的。n个根中只要有一个根(振荡模式)的实部大于零,系统将出现增幅振荡。若这个振荡模式的振荡频率对应于次同步谐振频率,系统将发生次同步谐振,使发电机轴系受到损害。这是通常研究次同步谐振的小干扰稳定理论。
在本文研究中,能使系统在平衡点x*处的特征根中出现一对虚根的参数,称之为分歧参数。这对虚根的出现,使系统非线性增强,平衡点附近显现出非线性奇异特性,即出现非线性振荡。对此,研究次同步谐振的小干扰稳定理论无法分析。
2 非线性振荡分析
分析非线性振荡的关键是要明确非线性振荡的性态,也就是要判断非线性振荡轨道是否稳定。轨道稳定的情况对应于系统由初始增幅振荡跃变为小模等幅振荡的情况,这将缓解次同步谐振。轨道不稳定的情况则对应于系统由初始渐近稳定跃变为增幅振荡的情况,不应出现的次同步谐振将出现。本文采用中心流形理论和分歧理论来分析这种非线性奇异现象。首先利用中心流形理论把式(1)的高维非线性系统约化到凝缩了全部必须的非线性特性的二维分歧方程上,再用分歧理论来分析非线性振荡的性态。
2.1 中心流形理论
中心流形上的流形性态与线性化中心子空间上的流形的性态不同,中心流形上的流形的局部性态,可以有效反映出原系统的有关非线性特性。所以要研究一个复杂高维非线性系统的平衡点附近的性态,可以首先利用中心流形理论将这个高维非线性系统约化为一个含有中心流形的低维子系统。研究这个低维子系统就等价于研究原高维非线性系统,而研究这个低维子系统要容易得多。这样,中心流形理论就为非线性振荡分析提供了有力工具。
对式(1)的状态变量x作线性变换,即

式中U为A阵的右特征向量矩阵。将式(1)所描述的非线性系统分化为2个子系统,即

式中:Js为稳定特征根所组成的对角阵;Jc为2个虚根所组成的对角阵,Yc=(y1,y2)T。
式(3)中第一个方程代表了属于局部衰减的子特征空间的动态特性,第二个方程就是分析非线性振荡性态的主要方程,称为分歧方程。它们所代表的非线性动态系统存在如下的局部中心流形:

在其临界点的邻域内,中心流形被分歧方程
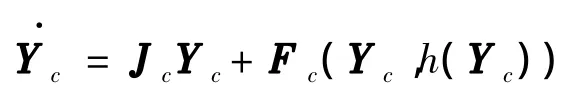
所控制,系统的所有非线性特性都将通过中心流形凝缩到这个二维的分歧方程上。
2.2 非线性振荡性态的确定
非线性分析理论的发展,使原来很难分析的非线性系统的动态特性问题有了行之有效的方法,这就是有限项泰勒级数的分析方法。这一方法不仅在小干扰下使用,在大干扰下也开始了应用[4]。就当前非线性振荡而言,研究分歧方程泰勒级数前3阶项,就能获得式(1)所代表的原系统动态特性的有关信息。分岐理论进一步指出,分歧方程泰勒级数3阶项中的系数就表明了非线性振荡的性态。实际上的系数就是分歧方程所代表的极限园的曲率系数β2。如果曲率系数β2小于零,非线性振荡就是轨道稳定的;如果曲率系数β2大于零,非线性振荡就是轨道不稳定的。
按文献[5],曲率系数β2的计算式如下:
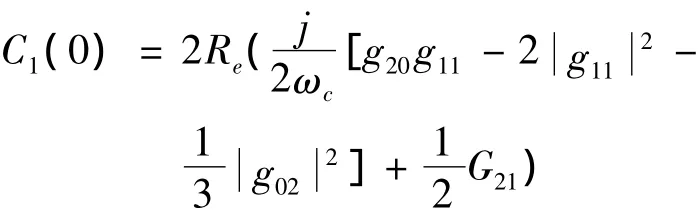
式中各参数的意义和求取见文献[5]。
显然计算曲率系数β2是一项非常复杂的工作,系统越大,计算越困难。n=2时可以用解析解法,只要系统维数n≥3,就只能用文献[5]提出的数值解法。
3 分歧参数对振荡性态的影响
在次同步谐振的分析研究以及工程实践中,所感兴趣的另一问题是分歧参数变化时,非线性振荡的性态能否改变,也就是说,分歧参数α变化时,曲率系数 β2将怎样变化[5-6]。当 β2> 0 时,如果∂β2/∂α 也大于零,则 α 增大,β2的符号不变,系统仍将是轨道不稳定的;若α减小,β2也将减小,这就可能使β2改变符号,也就可能使非线性振荡由轨道不稳改变为轨道稳定的。∂β2/∂α小于零以及β2<0时的分析与上述分析相同。
上面的问题实际上就是系统参数对曲率系数β2的灵敏度问题。由文献[5-6]可知,求取β2是相当复杂的,再计算β2对系统参数的偏导数就会更加复杂。这里仍用文献[5]提出的数值微分计算∂β2/∂α ,计算公式为
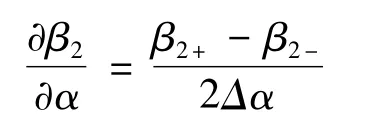
4 算例分析
4.1 算例计算
选定式(2)的 D1=3.59,D2=0.224,D3=0.224,D4=0,D5=0.145,其它参数见文献[3]。状态方程由10阶转子运动方程、2阶网络方程和3阶发电机暂态方程组成,系统总阶数为15阶。
1)当串补度为64 η0时,系统主要振荡模式为


式中λ12,13为共轭虚根,表明系统将出现非线性振荡。λ12,13虚部为 28.7 Hz,小于同步频率,在次同步振荡范围内。经分析可知,这是对应于低压缸和发电机间的扭振模式。
按本文所提方法,计算求得系统曲率系数β2=-0.122,小于零,表明这时的非线性振荡将是轨道稳定的。也就是说当串补度小于64 η0时,所有振荡模式实部小于零,系统将是渐进稳定的,和通常小干扰稳定分析的结果吻合。当串补度略大于64 η0时,λ12,13实部大于零,按通常小干扰稳定分析,系统将发生增幅振荡,就是次同步谐振。但由于现在的振荡还是轨道稳定的非线性振荡,所以系统将先显现出增幅振荡,随后将跃变为小模等幅振荡。这将使次同步谐振的破坏作用大大缓解。
这一分析的结论对工程实践很有指导作用。首先,它表明系统真正的不稳定域比通常次同步谐振分析的稳定域变小了。正如文献[1]通过数值仿真研究指出的,有时仅有按特征值方法计算出的15%~30%。其次,有时在较大的运行范围内,特别在高负荷条件下,这种小幅值的次同步振荡不会对机组轴系的疲劳寿命及整个系统的动态稳定性造成任何威胁。因此,在这种情况下,以往用系统线性化方法的特征根正负来判断系统安全运行范围的方法是非常保守的。
2)把D2减小为3.363 6,串补度改为67 η0,其它参数不变,系统主要振荡模式为
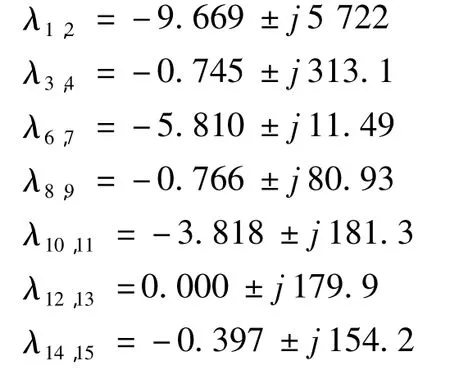
可以看出,λ12,13造成系统振荡仍然是非线性的。振荡频率约为28.3 Hz,仍在次同步振荡范围内。经分析知,这仍是对应于低压缸和发电机间的扭振模式。
按本文所提方法求得β2=0.16>0,表明出现的非线性振荡将是轨道不稳的。也就是说当串补度大于 67 η0时,λ12,13实部变正,系统将出现增幅振荡,次同步谐振出现,和通常小干扰稳定分析的结果吻合。串补度略小于 67 η0时,λ12,13变负,系统所有模式将都在S平面左半面。按通常小干扰稳定分析,系统应是渐近稳定的,不会出现次同步谐振。但由于非线性振荡的作用,使初始出现的衰减振荡很快跃变为增幅振荡,次同步谐振发生,并将对发电机轴系造成破坏。也就是说,次同步谐振不再是从S平面的右半平面开始的,在S平面虚轴左侧附近就已经发生。
上述观点是在通常小干扰稳定分析基础上,利用中心流形理论与分岐理论对非线性振荡研究后提出的观点,在次同步谐振分析领域中,是对通常次同步谐振分析的补充和修正。
4.2 数值仿真验证
1)为验证上述计算分析的正确性,取串补度为64.2%(略大于 64%,此时 λ11,12的实部为正),机轴上的输入机械功率增量为0.03(这大约为输入机械功率0.876的3.4%,可视为小扰动),其数值仿真结果如图2所示。从图2可清楚看出,系统初始出现的是增幅振荡,表明次同步谐振已经出现,这与小干扰稳定分析结果是相吻合的。但一段时间以后,增幅振荡变成了等幅小模振荡。从图3曲线可以测出,其振荡频率约为28.71 Hz,为次同步振荡频率。显然,这种变化已经缓解了低压缸与发电机间的扭转振荡,减小了对发电机轴系的损坏。这与4.1节的计算分析结果是相同的。

图2 轨道稳定的非线性振荡
2)再取串补度为67.01%,略大于前面计算时的67 η0。这时,系统特征根中 λ11,12的实部由 0变负,所有其它根也都位于S平面左半面。扰动仍为加在机轴上的输入机械功率增量,大小为0.03。数值仿真结果如图3所示,可以看出,初始衰减的振荡在几秒之后便很快跃变为增幅振荡,轨道不稳的非线性振荡出现,即次同步谐振出现。由曲线检测出其频率为28.3 Hz。这与4.1节的计算分析结果是相同的。
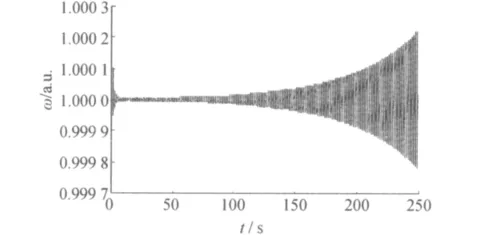
图3 轨道不稳定的非线性振荡
4.3 分歧参数对β2的灵敏度
当串补度为64%时,按本文所提分歧参数对曲率系数灵敏度的方法,取串补度为分歧参数α,在采用双精度计算时,取增量Δα=0.000 001,求得∂β2/∂α=11.081 554。这预示,随着串补度的增大,曲率系数也将增大,直至由64%时的负值变正,如果非线性振荡继续存在,轨道稳定的非线性振荡有可能变为轨道不稳定的非线性振荡。
同样可以分析系统其它参数对曲率系数的灵敏度,从而得出这些参数对非线性振荡影响的结果。
5 结论
由于系统分歧参数的变化和非线性振荡的出现,系统的强非线性有可能导致系统振荡的性态发生改变。本来是衰减的振荡有可能跃变为轨道不稳的非线性振荡,次同步谐振随之发生,而且是在虚轴左侧就已经发生;还有可能使在S平面右半平面虚轴附近的增幅振荡跃变为轨道稳定的非线性振荡,这种小模等幅振荡将大大缓解次同步谐振对发电机轴系的损坏。
[1]IRAVARI M R.Hopf Bifurcations in Torsional Dynamics[J].IEEE Trans.On Power Systems,1992,7(1):28 -36.
[2]蒋平,吴熙,TCSC对电力系统次同步谐振的影响[J].中国电力,2009,42(11):36 -40.
[3]ZHU W,MOHLER R R.Hopf Bifurcations in a SMIB Power System with SSR[J].IEEE Trans.On Power Systems,1996,11(3):1579-1584.
[4]邓集祥.大干扰下主导低频振荡模式的鉴别[J].电网技术,2007,31(7):36-41.
[5]邓集祥,刘洪波.多机电力系统非线性振荡的研究[J].中国电机工程学报,2002,22(10):67 -70.
[6]邓集祥,张新宇,童建东.系统参数对Hopf分歧影响的研究[J].电工技术学报,2007,22(9):130-135.

