有关复李群与A-李群的性质的初步探究
岳祥振
(伊犁师范学院奎屯校区 文理系,新疆 奎屯 833200)
有关复李群与A-李群的性质的初步探究
岳祥振
(伊犁师范学院奎屯校区 文理系,新疆 奎屯 833200)
文章从复李群、A-李群及其子群的定义和性质出发,研究了复李群G成为复Poisson仿射群的充要条件,并探讨了A-李群的积和A-李子群的交集的性质.
复Poisson仿射群;A-李群;A-李子群
文章着眼于超李群加以探讨,丰富了超微分几何的理论内容,同时也为量子物理等其他应用学科提供了新的研究工具.A-流形是流形概念的一个自然推广,A-李群也可看作是李群概念的一个自然推广.
1 基础概念与引理
定义1 如果复李群G为仿射群K(G,H),带有复结构J并赋予了Poisson结构π,使其成为Poisson仿射群.则称其为复Poisson G仿射群.简称为复Poisson仿射群,记为(K(G,H),π,J).
定义2[3]设M是一个拓扑空间,φ:U→O是M的一个坐标卡,其中φ是同胚,开子集U奂M,O是某A-向量空间E的偶性部分的开子集.在不产生混淆的情况下,用开集U奂M或 (U,φ)表示一个坐标卡.M两个坐标卡φa:Ua→Oa奂(Ea)0, φb:Ub→Ob奂(Eb)0是相容的,如果映射φaφb-1和φbφa-1是光滑的,即φbφa-1∈C∞(φa(Ua∩Ub);Eb)0和φaφb-1∈C∞(φb(Ua∩Ub);
Ea)0.
拓扑空间M的光A-结构是一坐标卡簇S={φα:Uα→Oα|α∈I}:满足下面三个条件:

(2)坐标卡簇S中任意两个坐标卡是相容的;
(3)若坐标卡φ:U→O与坐标卡簇S中的元素全部相容,则φ∈S.
proto A-流形是带有光滑A-结构S的拓扑空间M. proto A-流形的册是S的子集U,如果它满足条件(1)和(2),但不必满足(3).
定义3 设G、H是A-李群,映射ρ:G→H称为A-李群同态,如果ρ是光滑的且它是抽象群的同态.
定义4 如果G是A-李群,G的一个A-李子群是一对(i,H),使得H是A-李群,且i:H→G是内射的A-李群同态.在一般情况下,仅用H表示G的A-李子群.
引理1 设M和N是两个A-流形,U和V分别是M和N的册.在M×N上定义一个册
5-羟色胺再摄取抑制剂在妊娠期抑郁患者中使用的安全性研究 …………………………………………… 高 杉等(17):2439

其中定义(φa×ψb)(x,y)=(φa(x),ψb(y)).则M×N是一个A-流形.
引理2 给定一个拓扑空间M,坐标卡簇U={Ua|a∈I}满足条件(1)和(2).则册U定义了M的惟一的一个光滑A-结构.
2 主要定理及证明
定理1 如果复李群G为仿射群K(G,H),并在G上赋予了Poisson结构π,使其乘法满足Poisson映射.则复Poisson仿射群的充要条件是坌g1,g2∈G,h1,h2∈H

其中l(g1,h1),r(g2,h2)分别表示仿射群K(G,H)的左、右平移(不变向量场).
证明 先证必要性:设(K(G,H),π,J)是复Poisson仿射群,则乘法
m:K(G,H)×K(G,H)→K(G,H)是Poisson映射,即坌g1,g2∈G,h1,h2∈H,有

又m为全纯映射,根据乘积Poisson流形M×N的性质有

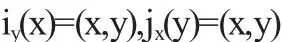
所以
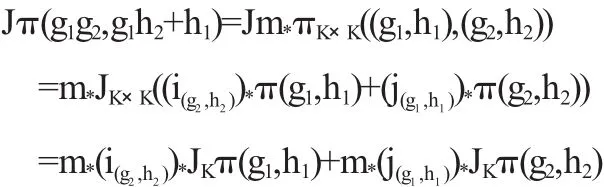

充分性的证明只需将上面的证明过程逆推即可.
推论1.1 如果(K(G,H),π,J)是复Poisson仿射群,e,θ分别是G和H的单位元,则Jπ(e,θ)=0,其中复李群G中的远算为“乘法”,H中的远算为“加法”.
定理2 设G1,G2是两个A-李群,在笛卡尔积G1×G2上定义乘法运算
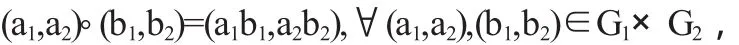
则G1×G2是一个A-李群.
证明 由引理1得G1×G2是一个乘积A-流形.设e1,e2分别是G1、G2的单位元,则(a1,a2)莓(e1,e2)=(a1e1,a2e2)=(a1,a2),坌(a1, a2)∈G1×G2.所以(e1,e2)是G1×G2的单位元.又(a1,a2)-1=(a1-1,a2-1)是(a1,a2)的逆.又由乘法运算得乘法是封闭的,故G1×G2是抽象群.因为G1、G2是A-李群,所以它们的乘法运算m1:G1× G1→G1和m2:G2×G2→G2是光滑的,其中mi(ai,bi)=aibi,i=1,2.设G1、G2的册分别为u={φa:Ua→Oa|a∈I}和v={ψb:Vb→Pb|b∈J},则φa1莓m1莓(φa2,φa3)-1和ψb1莓m2莓(ψb2,ψb3)-1是光滑的.定义m: (G1×G2)×(G1×G2)→(G1×G2)为坌ai,bi∈Gi,i=1,2,则 (φa1×ψb1)莓m[(φa2×ψb2)×(φa3×ψb3)]-1
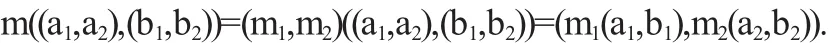

可见
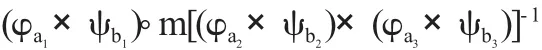
是光滑的.综上所述,G1×G2是一个A-李群.
定理3 设A-李群G,(i1,G1)和(i2,G2)分别是A-李群G的A-李子群.则G1∩G2是G的A-李子群.
证明 (1)先证G1∩G2是G的A-流形.取G的单位元e,由于G1,G2是G的A-李子群,所以e∈G1∩G2,G1∩G2≠覫.设G是构造于A-向量空间E上的A-李群,G1是构造于分级子空间Fi奂E(i=1,2)的A-李子群.记F=F1∩F2,易得F是A-向量空间E的分级子空间.取G的一个册w={φa:Ua→Oa奂E0|a∈I}.令

则S={ψa:Va→Pa奂F0|a∈I}必是G1∩G2的册.事实上,由于∪a∈IUa=G,且∪a∈IVa=G1∩G2,所以S满足条件(1).
再证S满足条件(2).任意取S中得两个坐标卡ψa:Va→Pa奂(Fa)0和ψb:Vb→Pb奂(Fb)0.由于φbφa-1:φa(Ua∩Ub)→Pb奂(Eb)0是光滑的,则φbφa-1到φa(Ua∩Ub)∩(Fa)0上的限制也是光滑的.又φa(Ua∩Ub)∩(Fa)0=ψa(Va∩Vb),故φbφa-1ψa(Va∩Vb)奂(Fb)0,所以φbφa-1:ψa(Va∩Vb)→(Fb)0是光滑的,故ψbψa-1:ψa(Va∩Vb)→(Fb)0是光滑的.同理,ψaψb-1:ψb(Va∩Vb)→(Fa)0也是光滑的.所以S满足条件(2).
再由引理2可知S惟一地确定了G1∩G2上的一个光滑A-结构.而G是满足第二可数的、Hausdorff的拓扑空间,所以G1∩G2也是满足第二可数的、Hausdorff的拓扑空间.因此可得G1∩G2是G的A-流形.
(2)单位元e∈G也是G1∩G2的单位元.易知G1∩G2是抽象群.
(3)由于A-李群G上的乘法映射m:G×G→G是光滑的,只需将m限制到(G1∩G2)×(G1∩G2)上,即可得到G1∩G2上的乘法映射m':(G1∩G2)×(G1∩G2)→G1∩G2,所以m'是光滑的.
(4)因为i1:G1→G和i2:G2→G都是内射的A-李群同态,不妨令i=i1|G1∩G2,则i:G1∩G2→G保持i1在G1上的运算.所以i是内射的A-李群同态.
综合(1)(2)(3)(4)四部分,可知G1∩G2是G的A-李子群.
推论3.1 A-李群G的有限多个A-李子群的交依然是G的A-李子群.
例 设G=Aut(E)是有限维的A-向量空间E的自同构群.在该群上定义了通常的复合“莓”这种群结构.Aut(E)的元素是右线性的,即Aut(E)奂EndR(E).在通常的复合“莓”结构下,Aut(E)对E的作用是光滑的左作用.Aut(E)是一个具有标准结构的A-流形,且是A-向量空间EndR(E)的偶性部分的开子集.它是一个A-李群.
〔1〕Boothby W.M.An introduction to Differentiable Manifolds and Riemannian Geometry[M].New York:Academic Press,1975.
〔2〕Serge Lang,S.Axler,F.W.Gehring,P.R.Halmos.Differntial and Riemannnion Manifolds[M].Beijing:Springer-Verlag (世界图书出版公司北京公司),1998.
〔3〕Gijs M.Tuynman.Supermanifolds and Supergroups(Basic Theory)[M].Kluwer Academic publishers,2004.
〔4〕Abraham R.A.,Marsden J.E..Foundations of Mechanics[M],2nd ed..Westview press,1978.
〔5〕孟道骥,白承铭.李群[M].北京:科学出版社,2005.
〔6〕陈维桓.微分流形初步(第二版)[M].北京:高等教育出版社,2001.
O152.5
A
1673-260X(2012)05-0001-02
伊犁师范学院院级青年科研项目(QN2008019)

