函数型数据分析的研究进展和技术框架
米子川,赵丽琴
函数型数据分析的研究进展和技术框架
米子川,赵丽琴
(山西财经大学统计学院,山西太原030006)
函数型数据分析(Functional Data Analysis,FDA)是1980年以后发展起来的一种基于离散统计数据函数化、进而通过函数型分析刻画更广义和更深刻统计关系的高维数据分析(Multivariate Data Analysis,MDA)方法。FDA的基本思想是由加拿大麦吉尔大学的J.O.Ramsay和牛津大学的B.W.Silverman等人提出并发展起来的,同时多位世界知名统计学者也对此作出了贡献。目前该方法已广泛应用于经济学、生物学、气象学、心理学、工业及其他领域。函数型数据分析的基本思想是把观测到的数据函数看作一个整体,而不仅仅是个体观测值的顺序排列,函数本质上是指数据的内在结构而不是它们直观的外在表现形式。因此,在简要回顾FDA发展历程的基础上,追踪国际国内主要研究动态,简介和评述FDA研究的技术框架以及与传统多元统计分析方法的差异,并试图就FDA在经济学中的应用进行一定剖析。
函数型分析;研究进展;技术框架
18世纪末以来,以Adolphe Quetelet、William Sleey Gosset、R.A.Fisher、K.Pearson等人为代表的新一代统计学家把传统的统计学带入了一个新世界,催生了包括回归分析、方差分析、相关分析、假设检验、时间序列分析等方法体系的相对完整的现代统计学学科体系和知识框架。100多年来,伴随着应用统计的不断深入,工业革命、计算机技术和互联网络三大革命也给统计学带来了全新的研究视野和方法论改进,极大地丰富了统计研究的工具和方法。但同时,统计学家们也注意到在传统统计分析中,几乎所有的方法都是以离散性的统计数据为研究起点的,其数据通常是一个时间序列、横截面数据或者它们的综合,即面板数据(Panel Data)。近20年来,当代统计学家更多地关注了面板数据的分析和应用,解决了数据样本容量不足、对很多经济指标估计难度大且影响复杂以及难以区分经济变量等方面的问题。有关数量经济学模型的理论研究和实证检验表明,现有的统计方法存在三个方面的局限性:一是以线性结构为模型的主要形式,限制了复杂经济变量的变化描述,不能真实地反映实际情况;二是过分依赖大量的经典假设,一旦假设遭到破坏,结论也就难以立足;三是数据生成过程的信息不足,导致模型的预报性受到极大约束[1]。
事实上,大多数经济活动的过程是一个连续的过程,这个过程生成的统计数据可以用一个类似函数的特征表达式来描述,而通过现有的统计手段所获取的信息往往是一个不连续的、片段的、离散的有界、有序、有经济意义的数列。从数学的观点看,这个数列所包含的信息远不如一个函数来得更充分和完善,于是数学家们首先想到了将这些离散的观察数据退化拟合成一个函数,然后利用函数的优良性质进行更为深入研究的新思路[2]3。
一、文献综述
1958年,美国普林斯顿大学教授、心理测量学创始人Ledyard R Tucker发表了《因子分析中函数关系的参数确定》一文,首次提出了函数型数据的概念和因子分析中确定函数参数的一些方法[3]19-23。50多年来,函数型数据分析的发展主要呈现两条主线:其一是利用传统数据分析方法在语言学等社会科学领域进行函数分析,此方法的代表人物是法国学者Cailliez、Pages和Dauxois、Pousse[4-5];其二是麦吉尔大学的Suzanne Winsberg和J.O.Ramsay在关于样条插值法的研究中发展起来的[6-7]。
1982年11月,J.O.Ramsay发表了《When the data are functions》一文(见加拿大《心理测量学》,第47卷第4期),提出了函数型数据分析的主要观点和方法体系,并从数学上对函数型数据分析的基本理论进行了表述和论证。1991年,J.O.Ramsay和C.J.Dalzell又发表了论文《函数型数据分析的一些工具》,进一步提出了函数型数据分析的系统工具。六年后,J.O.Ramsay和B.W.Silverman在统计分析的已有理论和方法的基础上,在《函数型数据分析》一书中对函数型数据进行了系统总结和阐述[8]313-317。这一系列开创性的研究,标志着函数型数据分析的研究又翻开了新的一页。
目前,国外函数型数据分析方面的主要代表人物是加拿大麦吉尔大学的J.O.Ramsay教授、英国牛津大学的B.W.Silverman教授、澳大利亚莫纳什大学的Rob J Hyndman教授[9]。他们的主要研究成果集中在近10年间,而主要内容集中在数学理论的介绍和推导、函数型数据的主要拟合方法(插值法、分布拟合和函数逼近等)、异常点的检验以及在心理测量、生物统计、海洋研究等方面的实证分析[10]51-53。
近年来,函数型数据分析的介绍和研究也引起了国内统计学界的关注。中国科学院组织影印出版了J.O.Ramsay和B.W.Silverman合著的《函数型数据分析》(2002)。目前,能够检索到的中文相关文献只有10余篇,这些学者包括严明义、朱建平、米子川等人[11-13],大部分是对国外文献的介绍和初步的实证研究,尚没有系统的研究和应用成果出现,特别是在经济统计方面的深入研究则更少。
二、函数型数据分析的基本概念
函数型数据分析方法是对传统统计分析方法的延伸和发展,以“化数为形”为基本特征,发掘了原始统计数据所蕴含的函数规律和由函数规律引发的计算和分析活动,这是函数型数据分析的最初概念。
先进的数据收集工具经常会搜集到一组连续型数据,如脑电图、肌电图、学习曲线、空间中的路径、连续时间上的主题回应,发声中产生的语音测量结果、生物测定数据等,图1中的曲线正是这样一组数据。图1中的曲线分别代表了某人以10种不同发音方式发出“啊、咔”声音时舌背的高度[14],显然可看出图中每一条曲线代表每种发音方式的舌背高度,在用中间的平均曲线来概括10条曲线的同时,还可以用某种方式来测量每条曲线相对平均曲线的变化。
图1中每条曲线代表一种发音方式;同一个音符重复发10次;平均曲线由同一时间内10条曲线上同一点的平均数计算得到,在图中用虚线表示;时间单位在区间[0,1]上任意划分。
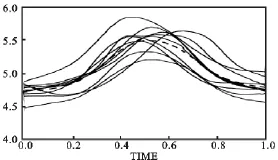
图1 400毫秒间隔内发出“啊、咔”声音时的舌背高度图

图2 统计观测的可能域图
图2提供了一个得出函数型数据概念的基本步骤。图2左上角是经典数据矩阵的域:有n个研究对象,每个对象都用p个变量描述,xij表示一次实验的结果;从左上角下移,这个域是当n趋于无穷时的情形,这时研究对象变成了总体;固定研究对象的数目允许变量个数无限增长时,就变成图2右上角所示的情形,这样针对每一个个体的变量描述变成连续变量,在图形上显示为线而不是点,自然可用符号xi(t)表示连续数据集上第i个个体在t点上的值;右下角域是表示研究对象和变量数目都趋于无穷时的情形,而本文的研究仅限于有限个体数目n的情形。
针对连续函数,传统的统计方法倾向于用两种方法来处理:
第一种是对连续集在一个有限数的点集tj,j=1,…,p上取样。在传统多变量分析中,每个点可以当做一个样本点来处理。然而此方法有很多缺点,即将函数型数据中很重要的连续性和高阶光滑性特征忽略了,采样点之间的信息缺失,协方差参数随着p的变化而迅速变化,即使压缩信息也不能降低模型的复杂性。
第二种是假设一系列的函数来近似数据,但是这些函数受参数个数的约束。有关研究曲线和项目特征曲线的文献对这个过程有很好的说明,尽管如此,这个方法还是出现了大多数参数曲线族缺乏灵活性的问题,不过样条函数技术的出现使该问题有了很大的突破。然而,在一个参数空间以点的形式概括数据同直接以函数的形式来概括还是不同的,当人们试图以函数形式而不是点的形式来表达函数型数据的变化时,这个问题就变得特别明显。
熟悉函数型数据分析的关键是用函数型分析的术语来表达传统的统计思想,而所涉及的思想是将数据定义成一个映射而不是点集,也就是说必须将数据看作是由域空间到列空间的可能的函数空间的元素。在多变量情形下讨论这种方法后,再将其放在函数型数据的框架下研究,最后再以这种观点来考察最小二乘估计、主成分分析和典型相关分析。在每个例子中由传统的多元数据过渡到函数型数据是非常简单的,基本上只需用积分来代替求和就可以了,而最重要且最困难的一步应该是将概念从静态到动态的转化。
三、函数型数据分析的数学准备
(一)向量空间
向量空间是一个实数的集合,它可以根据一般的加法法则进行加法运算,也可与数或标量相乘进行乘法运算。标量相乘等同于向量间的加法运算。在向量空间下,任意两个函数的和仍是连续函数,其和也在集合之中。由于函数是有关向量的值,所以函数可以与标量相乘,这样就保留了连续性,以保证其和仍然在空间中;函数空间包括了由有限个特别函数的线性组合生成的函数所组成的有用的有限维子空间。因此,p-1元多项式是连续性函数空间的一个p维子空间。
一个特别有用的向量空间形式是当其被赋予内积运算的情况。内积是对称且参数为线性的两个向量的实值函数,在其参数均为非零向量时,两个向量的内积为正数。两个p元的内积或标量积最为常见,在平方可积函数的空间中,两个函数乘积的积分代表内积。在以函数型分析的观点来讨论数据分析时,p维向量空间的p元数组与定义在闭区间上的实值函数的向量空间是对应的,其中实值函数的平方有限可积。
(二)P维向量数据
令X代表观测值Xij(i=1,…,n,j=1,…,p),X可以被看作是由一个向量空间到另一个向量空间的函数或映射。问题中涉及的两个向量空间是:
1.p维个体空间E。在这个空间中,任何观察到的或是假设的主题对象可以由p个变量所对应的某一点来表示。空间中的两个向量ej和ek的内积为bE=(ej,ek),简记为。向量e的模‖e‖是e和自身内积的平方根。该空间可看做p个正交向量e的集合。
2.n维变量空间F。在这个空间中,任何观察到的或假设的变量可以由n个个体在该变量上的值来表示。它也有内积bF(.,.)和n个正交向量集[15]。
(三)函数型数据
可以将上述关于函数型数据分析的讨论扩展到个体或个例是函数xi(t),0≤t≤T的情形。正如图2所示,人们可以想象,当变量的数量足够大、以至于下标j(j=1,…,p)可按连续数处理时,将其改写为t。t在本文中将被认为是时间,因为在实践中这种情况比较多见,在传统情形下对j求和转变为对t求积分。数据仍然用X来表示,但不再是矩阵,而是在下面的空间中定义了相应的映射。
1.无限维的个体空间E。任意观察到的或假设的个体都可以表示为函数e(t),由于函数有无限个变量的可能,空间就可能有无限维度。函数ej(t)和ek(t)的内积bE=(ej,ek)可以由式(1)给出:
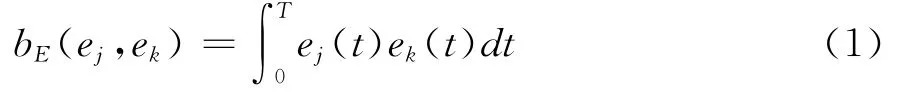
同样的,函数的模是由函数同其自身的内积给出,即是其平方的积分。如果模有限,则得到的空间称为希尔伯特(Hilbert)空间。希尔伯特空间的一个基本性质是空间中的任意一个元素可表示为空间中有限个正交函数的加权和,所以虽然维度是无限的但它至少是可数的。P个变量情形下的空间E也是一个希尔伯特空间。
2.n维时间空间F。这个空间与p个变量情况下的空间F有着完全一样的性质。在这个空间中,观察到的或是假设的任意时间点都可以由该点上的n个函数的值来表示,则X表示的映射是:
(1)X∶E→F。令e(t)为空间E中的任意函数。向量f的第i个元素由式(2)给出:

向量f是n维的,因其在F中。注意到这与p个变量情形在形式上是等价的,只是用积分来代替乘积Xe中元素的求和运算。因此,函数型数据情况下将X想象成一个拥有完全紧密的行的矩阵是非常有用的。
(2)Xt∶F→E。令f为空间F中的任意向量,则函数:

是E中的一个元素。此外,很容易看出对任意e∈E和f∈F均有bF(Xe,f)=bE(e,Xtf)。因此,用符号Xt来表示这个映射是有道理的。
(3)V∶E→E。同样的,由式(2)将函数e(t)映射到F中,再将得到的n维向量通过式(3)映射回E中,这个过程可由算子V=XtX来描述。当一个对称阵的秩足够大时,它就表现为拥有完全紧密的行和列,详细过程如下:

注意到V是由式子∫K(t,u)e(u)du所代表的积分变换的一般形式中的一个,其中函数K(t,u)被称为变换的核函数。在此例中K(t,u)=∑xi(t)xi(u)。
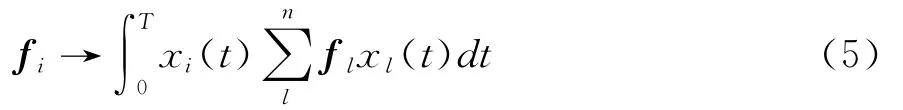
(4)W∶F→F。将空间F中的向量f映射到E中,再映射回F中,得到向量的第i个元素是:这些映射仍然可以由对偶图(1)来概括地表示。由变换X决定的E在F中的投影通常是n维的,因此与F本身是一致的。然而,这并不意味着W将向量f映射到它本身,现在的核心问题是研究任何一个或者所有这些映射作用的结果。
四、用函数型分析语言表示的最小二乘法逼近
传统统计过程的关键思想是通过用子空间中的点来逼近一个点集的方法以达到降维的目的。例如多元回归就是这样一个过程,即将空间中的元素投影到使用预测的变量fj(j=1,…,k)扩展而来的k维子空间中,投影为^f。因此,投影^f为f在子空间上投影的结果,可以将^f认为是投影算子P作用于f,这里的P可将任意向量映射为子空间的最小二乘投影。映射算子有两个重要的性质:PP=P和Pt=P。术语“算子”在最小二乘中有独特应用,需要满足:其一,被估计向量是希尔伯特空间的元素;其二,估计值在闭的子空间或是凸子集上。
在传统p个变量的数据分析中,逼近问题通常用变量矩阵F表达。然而,在函数型数据的情况下,把逼近问题考虑成用E中一个有限维的子空间的投影去逼近空间中E的一个函数e(t)。这个过程类似于电气工程师对输入信号运用滤波器以排除不需要的信息,也类似于数据分析师用比较简单的函数的线性组合来估计复杂函数的过程。当逼近的目标为‖e(t)-^e(t)‖2=∫[e(t)-^e(t)]2dt最小化时,所对应的映射即是算子P。
近似函数的集合是逐段多项式或样条函数,这类函数具有灵活性强、参数个数适中、易于计算等良好性质。Winsberg和Ramsay一直在致力于研究单调样条函数[16-17]。这种方法将函数空间投影到一个圆锥上,在处理更广泛的问题时很容易。关于样条插值方法的更全面的处理和相应的不同空间的知识可以在Schumaker的成果中找到[18]77。
五、函数型主成分分析
从函数型分析的观点看,主成分分析问题本质上是映射V∶E→F或是X∶E→F。因此,寻找映射^V或者^X,并使其在某种程度上与所要逼近的值尽可能地“接近”。“接近”可以理解为映射近似的结果应尽可能地与其真值接近。这里映射逼近的问题可以简化为映射在列空间中的逼近,因此可以应用前文讨论过的最小二乘的方法来研究。
对X映射的结果可以概括为E中具有单位模的向量e映射到F中的过程,于是在F中的投影的模为‖Xe‖。由于X的映射是线性的,所以E中单位球在F中的投影是一个椭球。图4是由图3中的3 ×2矩阵得到的单位圆投影。因此,在F中的投影‖Xe1‖的模最大,在E中所对应的元素e1的位置可以被看作是超椭球体的最佳一维近似。投影的模最大且与e1正交的元素e2的位置是椭球体的最佳二维近似。这个过程可以一直迭代下去,一直到E的维度被耗尽为止。
根据上文所定义的变换有:
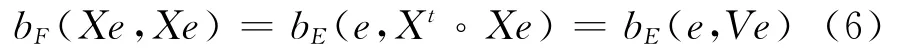
因此,寻找具有单位模且能使‖Xe‖最大的向量e的过程相当于寻找使bE(e,Ve)最大的元素e,因为任意内积满足柯西-施瓦茨不等式:
bE(ej,ek)2≤bE(ej,ej)bE(ek,ek)
因此当满足如下条件时:

bE(e,Ve)达到最大值。很显然上式是一个特征方程。由式(7)可知‖Xe‖2=λ,因此λ是F中变异的测度。可以认为Xe定义了E在F中的投影或是F在映射W下投影变异的主方向。在较一般的情况下,算子V可以表达为有限可数项∑λjej(u)ej(t)的形式,其中(λj,ej)是方程(7)的特征方程的第j个解。

图3 由x映射的单位圆转换图
特征方程的求解过程称为谱分析,它是函数型分析中的一个核心主题。在有限p维的情形,e是对称正定矩阵V的特征向量。在函数型数据中e(t)是算子V的特征函数。任何时候λ都是V的特征值。实际中,在更一般的条件下,特征方程解的数量有限可数,特征值非负且不同,最大特征值是有限的。
有很多计算特征方程ej(t)问题的方法。当n不是非常大时,可用矩阵W的矩阵特征分析并代替,所需的特征方程简化为Xtfi,i=1,…,n。直接处理算子V的技术也是存在的,在收敛的情形下,可以引入不连续的近似方法。对算子V的不连续近似的一个简单形式是在[0,T]的间隔点中选择一个足够大的数,通过相应的被不同点分割的部分求和来逼近式(4)中的积分。在这种形式下,问题就变成了经典多元分析中的主成分分析。不过,越是复杂的正交过程所需要的分割点越少。
主成分分析的一个重要扩展是按照图4所示,当E被映射到另一个空间G的情况:

图4 对偶图
当G是E的子空间或是凸子集时,产生了一个特别重要的例子,即如G可以是由一系列样条函数扩展而成的空间的组成部分,或是一个圆锥,这个圆锥是组成单调样条函数凸组合的一部分。在这个例子中U和Ut将是投影算子P。主成分分析问题重新定义为在‖g‖=1的条件下求‖XUg‖的最大值的问题。
六、函数型数据的描述性统计
一个函数集的位置可以通过个体的逐点平均来概括。如果函数的组成中有一大部分是没用的信息,或是有不需要的非光滑成分,最好先用适当的样条函数逼近,再对样条函数求平均。原始函数可以通过减去它们各自的平均函数来中心化。
对离散程度的概括更为复杂,就好像不能用单个变量的变差来表示多元分布的整体变差一样,用逐点的方式来测度函数的变差也是没有用的。多元分布的离散程度可以由方差-协方差矩阵n-1XtX来表示。同样的,函数型数据情形下的方差-协方差算子n-1V也包含了函数变化的重要信息。算子的核函数K(u,t)=n-1∑xi(t)xi(u)定义了一个方差-协方差面,用轮廓图或透视图技术来描述这个表面是很有启发性的,而由K(u,t)/[K(u,u)K(t,t)]1/2定义的相关表面也可以由图形表示。正如多元分析中特征向量表明了变差的主要方向一样,与主导特征向量相对应的特征方程ej(t)也表明了相对于平均函数和函数变差的主要类型。
在这个问题上,分析时间序列所用到的技术可以同这里的函数型数据的分析联系起来,而这些过程都基于协方差结构是平稳的前提,意味着这里的相关表面K(u,t)可以单独定义为|u-t|的函数[20]339-341。由此可以发现,这种情形下的特征方程具有周期性,因此可以表示为有限个正余弦函数的组合。
函数型数据的描述性分析可以由图1所示的曲线来说明:图1中虚线显示了逐点平均曲线。注意到在t=0.4和t=0.8的时候舌背高度的变化速度明显变慢,并在t=0.5时达到了最高点;图5显示了这些曲线的方差-协方差表面,从右下到左上的对角线表面的高度显示了时间段内曲线上每一点的方差。两个峰值对应于t=0.4和t=0.8时的两个减速点;图6显示的是相关表面:表面上的两个深谷对应于两个减速点,表明舌背高度接近于零相关,表明舌头启动容易,但慢下来较为困难;图7给出了前两个特征向量:其特征值累计贡献达到了95%。概括地说,就是变差的主要模式有两种:一种表现为函数的大体垂直移动;另一种表现为在达到最大高度之前的爬坡和在到达最低高度时的向上调整。

图5 由图1中数据计算得到的方差-协方差算子K(t,u)的前两个特征函数图
前文图1中,对应于特征值分别为0,17和0,12时,占所有特征值比例95%。第一个特征函数表明了相对于平均函数的主要离差形式表现为垂直移动;第二个特征函数所代表的变差表现为在达到最大高度之前的爬坡和在到达最低高度时的向上调整。
七、典型相关分析
以函数型分析的术语来描述典型相关分析可以处理一系列的问题,因为典型相关分析涉及了许多项用于多元数据分析的常用技术。现在假设有两个子空间E1和E2,在每个空间中,每个个体由变量集或时间点来确定。
让X1和X2分别代表确定映射E1、E2到F的两组数据集,然后考虑F中的两个子空间:第一个子空间F1是F在算子W1=X1Xt1下的投影;第二个子空间F2是F在算子W2=X2Xt2下的投影。对应于这两个子空间的是投影算子P1和P2,两个算子分别将f的任意元素映射到子空间F1和F2最小二乘估计值上,这种情形可以由简化的对偶图来概括(见图6):

图6 对偶图
典型相关分析可以表达为对F1∩F2的描述。为了强化分析,需要加入的额外条件为子空间是闭空间,即维数有限。F中的一个任意元素f如果可以先由投影算子P1投影到F1中,再由投影算子P2投影到F2中,那么它将被映射到交集空间中,则意味着算子P1P2(或P2P1)提供了所需的映射。
在一般的情形下,典型相关分析简化为对P1P2作谱分析。在E1和E2的维数分别为有限值p和q的情况下,典型相关分析即可以简化为对)做特征分析。
表达典型相关问题时引入算子乘积的谱分析,这显然对于变量或函数的任何数量的集合都是通用的。因此,对k个表的典型相关分析可以转化为P1P2,…,Pk的特征分析。
当个体的数据表现为一对函数时,通常涉及到的投影不再是F的闭子空间。在实际中这意味着函数的两个集合可能在任意小和弯曲的部分上高度相关。针对这个难点的处理方法是将每个函数空间投影到合适的子空间或是有限维的凸集^E中(维数小于n),这可以看作是过滤数据的过程。利用一个投影是其自身的转置这样一个事实,其结果由对偶图表示(见图7):
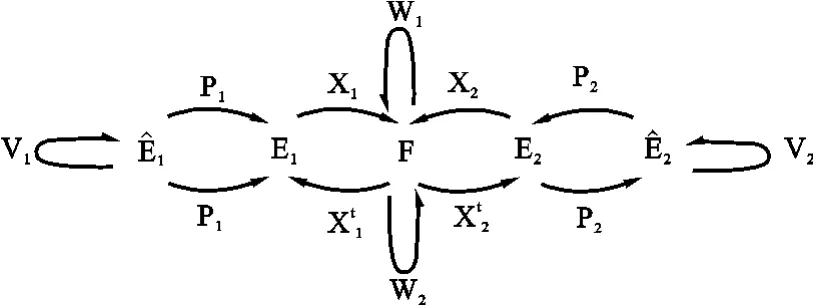
图7 对偶图
一般地,算子Vk=PkXkXtkPk(k=1,2,…),有逆算子,分析过程仍如上。在函数型数据的情形下,自然地可以考虑在对偶图中转换E和F的角色。当个体被分为两个或多个组时,会对成对的函数感兴趣,这时每一对函数都是一个特定组中函数的加权和,在满足正交条件时,这些特定组具有最大相关性。在p个向量的情形下,因为变量的顺序通常是任意的,所以人们很少对这个分析感兴趣,但在时间点的情况下,这个分析就变得非常有用。
八、结 论
从某种意义上说,广义的经济统计数据或者科学实验数据,基本上都可以看做是函数型数据,这样一来,有限数据集和无限数据集就不再有显著差别,相应的函数型分析就都可以顺利进行。用函数型分析方法也可以对其他熟悉或不熟悉的方法进行分析,如对偶度量(dual scaling)或对应分析、连续函数向量值的数据集、任意模式数据的列联表分析。已有的统计学的分支—贝叶斯推断,就是用函数型分析的术语来表达的。贝叶斯推断本质上是由一个定义在参数空间上的密度函数利用数据集所决定的非线性算子,并将其映射到自身的空间,在这个意义上算子V仅是一个特例。贝叶斯推断已经成为统计学最前沿的一种研究技术,并已在很多领域得到了广泛应用。
目前,从国内的情况看,函数型数据分析及相关应用研究刚刚起步,尚未形成稳定的研究团队和研究方向,对于统计学教学、科研及研究生培养方面的探索也处于起步阶段。有两个方面的趋势值得注意:一是国内数学和统计学界强有力的研究力量已经较为成功地开始了这个方面的研究;二是统计学一级学科的设立对于推动理学门类下统计学的繁荣和发展奠定了更广义的基础和发展空间。就函数型数据分析的基本框架和学术基础而言,目前的学科布局更有利于函数型数据的发展;同时,函数型数据分析的研究也将有利于统计学在更广义的方法论空间,从经济学、管理学、社会学等学科获得积极的方法突破和更加有效的应用成果。
正如Dieudonne在《Foundations of Modern Analysis》(《现代分析基础》)一书中所论述的:“学生应该尽早熟悉函数f只是单一个体,它本身可能是变化的,可以看作是函数空间中的一点;传统和现代分析方法的主要区别在于:在传统数学方法中,f(x)中的f是固定的,x是变量;而现代方法中,f和x都可以是‘变量’……”。
对于一个学科的发展来说,函数型分析无疑将成为一个学术热地,并为统计学及众多分支学科提供分析工具和更广义的应用。
[1] 米子川.依数据进行统计建模的三个基本分析层次[J].统计教育,2010(10).
[2] Aubin J P.Applied Functional Analysis[M].New York:Wiley,1979.
[3] Tucker L R.Determination of Parameters of a Functional Relationship by Factor Analysis[M].Psychometrika,1958,23.
[4] Cailliez F,Pages J P.Introduction dl'Analyse des Donn~es[R].Paris:Sociale de Mathsmatiques Appliqu6es et de Sciences Humaines,Prue Duban,75016Paris,1976.
[5] Dauxois J,Pousse A.Les Analyses Factorie Ues en Calcul des Probabilit6set en Statistique:Essai D'atude Synth6tique[R].Those d'btat,l'University Paul-Sabatier de Toulouse,France,1976.
[6] Winsberg S,Ramsay J O.Analysis of Pair Wise Preference Data Using Integrated B-splines[J].Psychometrika,1981,46(2).
[7] Winsberg S,Ramsay J O.Monotonic Transformations to Addictively Using Splines[J].Biometrika,1980,67(3).
[8] Ramsay J O,Silverman B W.Applied Functional Data Analysis:Methods and Case Studies[M].New York:Springer,London,2002.
[9] Rob J Hyndman,Han Lin Shan.Rainbow Plots,Bag-plots and Box-plots for Functional Data[R].Monash Econometrics and Business Statistics Working Papers,2009.
[10]Kreyszig E.Introductory Functional Analysis with Applications[M].New York:Wiley,1978.
[11]严明义.函数性数据的统计分析:思想、方法和应用.统计研究,2007(2).
[12]朱建平,王桂明.函数数据聚类及其在金融时序分析中的应用[J].统计与决策,2010(9).
[13]米子川.统计数据的函数化及函数型数据分析的工具创新[R].国家统计局全国统计科研项目2009年度重点课题研究报告,课题编号2009LZ026.
[14]Keller E,Ostry D J.Computerized Measurement of Tongue Dorsum Movements with Pulsed Echo Ultrasound[J].Manuscript submitted for publication to Journal of the Acoustical Society of America,1982.
[15]Pages J P,Tenenhaus M.Geometry and Duality Diagram.An Example of Application:The Analysis of Qualitative Variables[R].Paper Presented at the Psychometric Society Annual Meeting,Montreal,Canada,1982.
[16]Winsberg S,Ramsay J O.Monotone Spline Transformations for Dimension Reduction[J].Submitted for Publication in Psychometrika,1983,48(4).
[17]Winsberg S,Ramsay J O.Monotone Spline Transformations for Ordered Categorical Data[R].Paper Presented at the Psychometric Society Annual Meeting,Montreal Canada,1982.
[18]Schumaker L,Spline Functions:Basic Theory[M].New York:Wiley,1981.
[19]Doob J L.Stochastic Processes[M].New York:Wiley,1953.
The Research Development and Technical Framework of Functional Data Analysis
MI Zi-chuan,ZHAO Li-qin
(School of Statistics,Shanxi University of Finance and Economics,Taiyuan 030006,China)
Functional Data Analysis(FDA)has been developed into a Multivariate Statistical Analysis(MSA)method based on thoughts of converting discrete data into functional ones since 1980s,which portrayed more generalized and more profound statistical relationship through the functional analysis.The basic idea of FDA is brought up by James O.Ramsay,aprofessor of Canada McGill University and Bernard W.Silverman,from Oxford.Many other world-famous scholars have contributed to the idea.The method is now widely used in economics,biology,meteorology,psychology,industry and other fields.Functional Data Analysis regards observed data as a whole,but not just the order of the individual observations.Functions essentially refer to the inner structure of data,but not their intuitive form.This paper briefly reviews the development history of FDA and tracks domestic and international research trends.It introduces the FDA research technical framework and the differences between FDA research technical framework and the traditional method of multivariate statistical analysis.Attention focus on the application of FDA in economics.
functional analysis;research progress;technical framework
book=13,ebook=52
O212.4
A
1007-3116(2012)06-0013-08
(责任编辑:郭诗梦)
2011-11-30;修复日期:2012-04-18
国家统计局全国统计科研项目2009年度重点课题《统计数据的函数化及函数型数据分析的工具创新》(2009LZ026)
米子川,男,山西祁县人,统计学博士,副教授,统计学、应用统计专业硕士和MPA导师,研究方向:应用统计和经济统计;赵丽琴,女,山西原平人,统计学博士,副教授,研究方向:经济统计学和多元统计分析。

