文化数学三题（之三）试论文化数学的建构途径

广东省深圳市教育科学研究院 尚 强 胡炳生 （邮编：518001）

文化数学，其主要想法就是：用文化的各种元素对数学进行包装，使数学文化化.将数学从科学课程转变为文化课程.构建文化数学，可以设想有以下途径：

1 数学与历史结合

数学，从数学的历史故事和历史上有关数学的逸闻趣事讲起.例如，讲概率，可以从赌徒梅累提出的得分问题说起，讲到帕斯卡和费马解决此问题的不同思路.这比从定义到定理、公式纯理论的讲法，一定会有趣得多.故事如下：

在17世纪的法国，有个深有文化素养的赌徒梅累，在赌博中遇到一个棘手的问题：得分问题.

这先要了解当时欧洲赌博游戏的规则：一般是两人的对奕，双方各出同等赌资，放在一起作赌注.每局胜者得1分，事先约定先得几分者为胜，胜者获得全部赌资.梅累遇到的得分问题是：A、B二人各出金币32枚作赌注.约定先得4分者获胜，获得全部64金币.但是由于某种突然情况，当A得2分，B得1分时，赌博不得不终止.试问：这时应该按照什么比例来分配这64枚赌金？

梅累虽然是一个熟练的赌徒，但是不能解决这个从未遇到过的难题.于是他向法国天才数学家——帕斯卡（1624－1662）求救.而帕斯卡又把这个问题写信给他的朋友，被誉为业余数学家之王的费马（1601－1665）.

经过思考和研究，帕斯卡和费马从不同的思路上给出了各自的解法.

费马的方法：设想赌局继续进行4局，总可以得出最后结果.他列举出各种胜负可能情况，以决定个人的胜负可能性：

1.A胜4局，B全 负，这 只 有 一 种 情况 ——aaaa；

2.A胜3局，B胜1局，这有4种情况——aaab，aaba，abaa，baaa；

3.A胜2局，B胜2局，这有6种情况——aabb，abab，abba，baba，bbaa，baab；

4.A胜1局，B胜3局，这也有4种情况——bbba，babb，abbb，bbab；

5.B胜4局，A全负，这也只有一种情况 ——bbbb.

以上共有16种情况，其中有11种情况为A胜；其余5种情况B胜.从而A、B二人的胜率（机会）之比为11∶5.

因此，A应得赌金的11／16；B应得其余的5／16，即A应得赌金的×64＝44个金币，B得×64＝20个金币.

帕斯卡则从从他发现的数字三角（帕斯卡三角）出发，设想：赌局开始，在数字三角的顶点上放一颗棋子，第一局若A胜，将棋子向左下移到第二行；若B胜则向右下移动棋子到第二行.第一局后，不论谁胜，棋子都会移到第二行.第二局后，棋子一定回移到第三行上.只是若A胜棋子向左下移一格，B胜向右下移一格.依次类推，第三局，棋子移到第四行.第四局后，棋子移到第五行.

例如，若A胜3局，B胜1局，则棋子向左下移3次，向右下移1次.棋子移动的路线有以下四条：

1（向左）→1（向左）→1（向左）→1（向右）→4；

1（向左）→1（向左）→1（向右）→3（向左）→4；

1（向左）→1（向右）→2（向左）→3（向左）→4；

1（向右）→1（向左）→2（向左）→3（向左）→4.

则不论如何，最后棋子都移到第五行的第二个数字4上.这个数字4，就是A胜3局，B胜1局的所有可能情况.

同理，第五行上第三个数字6，就是从顶点1移动棋子到这个数字上的可能情况总数.

因为A若胜4局、3局、2局，A都先胜4局，故A胜；若A只胜1局，或全输，B才能够获胜.

因此，对应第五行上的前3个数字1，4，6就是A获胜的所有可能情况；而第五行后两个数字5，1则是B获胜的所有可能情况.于是A、B获胜的可能机会之比应为：（1＋4＋6）∶（1＋4）＝11∶5.这与上面费马的结果完全相同.

到此，梅累的得分问题，便彻底解决.

若用排列、组合符号表示，那么上述结果可以表示为：

比较两人的思路和解法，虽然后者思路要复杂一些，但是利用排列组合，可以将以上问题的解决，推广到一般情况.例如，A、B二人各需再胜m局、n局，那么，终局的棋子应该落在第m＋n＋！行上，且二人获胜机会之比为：

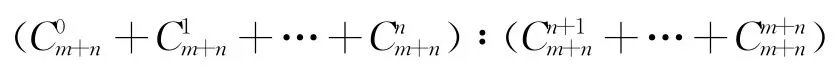
由此，可以引出排列、组合的课题.然后即可进入概率的正题.这样从数学事件和故事开始，可以引起学生学习兴趣.

若对于初中学生讲，则不必一次讲完，先讲个故事的大概.只作为引子，总是可以的.目的在于引起学生求知欲望.

2 数学与文艺结合

数学，从数学诗歌、数学图画讲起.例如，从孙子问题和孙子歌讲起，引导出同余和同余式.又例如，从哥斯尼堡的七桥图画，引导图论的意义和有关知识.

例如，可以引唐代诗人王之涣“登鹳雀楼”诗句“欲穷千里目，更上一层楼”发问？更上一层楼，就能看到千里之外的景色吗？——不能.那么“欲穷千里目，须上几层楼”呢？这就变成一个有趣数学问题.可以引出勾股定理、几何圆的有关知识和求解二次方程等数学知识.也可以引导学生自己来思考和解决；或者师生共同探讨解决.

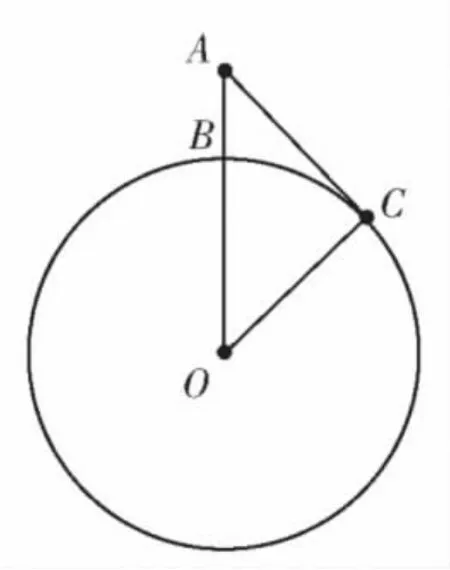
图1－1

首先将实际问题抽象化.把地球抽象成一个球，而将高楼和人的视线所在的地球截面假设为一个圆.如图1－1所示，高楼为AB，O为地球球心，人的视线为AC.连接OC，构成直角三角形ACO.再设地球半径为R＝6370km，楼高为x，依据勾股定理，便有关系式：AC2＋OC2＝AO2即 5002＋R2＝（R＋x）2，或x2＋2Rx－5002＝0.将R＝6370代入上式，得x2＋12740x－250000＝0.这是一元二次方程，据求根公式，便求得其解为：x≈16（km）.假如每层楼高度为4m，那么，该楼就有4900层.按照这位先生的计算，那么，王之涣的这首诗的后两句，就要改成“欲穷千里目，须上四千九百层楼”，另外还要加注解：“假设每层楼高4m”.

3 数学与生活结合

数学，从生活中的实际问题讲起.小学生识数教育，可以从民间谚语“凡事要作到心中有数”说起.认识数字“3”，可以从《三字经》中：天地人“三才”，日月星“三星”等说起.

讲概率，从机会说起.举出学生生活中的关于投掷硬币、掷骰子和彩票中奖等例子.和学生一同探讨和分析研究.然后再上升到一般理论.

几何作图，可以与几何商标图形进行联系.要学生举出他见到的集合图形商标的例子.举出典型的著名商标，来加以讨论，以此来引出几何作图的意义和作法.例如经常见到的下述几何商标图形，不加说明，学生都能说出它们的商标名称.

面对这些几何图形商标，可以问学生，这些几何商标是什么几何图形？是如何制作的？有什么特点？有什么文化意义？由此，可以说明几何作图的意义和基本几何作图，几何作图规范作法.进一步，还可以引导有兴趣的学生进行几何图形商标设计.例如，可以要学生为班级设计一个用几何图形表示的班徽.

4 数学与问题解决结合

数学，从问题解决的奇思妙想讲起.例如，不等式，可以从用等式“夹逼”出不等式的奇思妙想，来引起学生兴趣.关于概率统计，历史上的趣题很多.例如，可以从帕斯卡、费马解决“得分问题”，哈代解决“色盲遗传”的经典问题，引起学生对统计学的兴趣和惊喜.

我们来看看哈代是如何解决色盲这个难题的.

在20世纪之初，欧洲人发现人的色盲是能够遗传的.于是，有人提出怀疑：因为色盲遗传，是不是有一天全人类都会成为色盲呢？这可是个大问题.色盲虽然不是严重疾病，但是如果一个人是色盲，那么他就不能从事许多种职业.所以谁也不愿是色盲.不过，这是个极其困难的问题.要判断人的色盲遗传的可能究竟有多么大，会不会遗传给全人类，按照当时的科学水平，是不可能解决的，因为人的眼睛是人身体上最复杂的器官；同时，遗传性牵涉到遗传基因，而此时基因尚不知为何物.色盲的遗传性无从研究.那怎么办呢？人们把这个棘手的问题提到了英国著名代数学家哈代（1977－1947）面前，请他用数学方法来解决.哈代是个纯粹数学家，从不搞实际应用数学问题.而这次却破例答应试试看.他首先了解了关于人类的男女性别的知识：男女性别是由于本身的染色体不同决定的，男女都有23对染色体，其中有一对决定性别的染色体.这性别染色体，男性为“X，Y”，女性则是“X，X”.其次又对色盲遗传的情况，进行了调查.调查发现了人类色盲的遗传性有以下几个特点：

1.男女色盲都有；

2.但是女性色盲比男性色盲比例小得多；

3.如果母亲是色盲，那么所剩生的子女中，男性肯定是色盲，而女性则可能色盲，也可能不色盲.

根据以上实际情况，他进行分析后得出初步结论是：

第一，由于男女色盲都有，所以色盲肯定是性染色体中的“X”出了问题，即有缺陷的染色体“X”（不妨记为“X－”）是色盲的元凶.因为如果是染色体Y缺陷的原因，那么女性是不会有色盲的.

第二，为什么女性色盲比男性色盲少呢？——一定是因为女性有两个染色体“X，X”，如果其中一个有缺陷，另一个正常，它可以不色盲.因此，人只要有一个正常的染色体X，就不色盲.

于是，男人可以分为两类：F（正常）、S（色盲）；女人分为三类：Z（正常）、C（次正常）和K（色盲）.

为了使问题简化，我们可以作如下合理假设：

第一，在两类男子和三类女子之间的配对是随机的；

第二，异常染色体（X－）在男女人体中的比例相同，设为p（q＝1－p）；

第三，父母与子女两代人中的男女人数之比为1：1.

在这些假设下，父代男、女中的色盲比例分别为（p＋p2）／2.之所以被2除，因为男女都各只占总人口一半.

于是，父代中父母配对有以下六类：

（1）（F，Z）—— 父母均无色盲；

（2）（F，C）—— 父亲正常，母亲次正常；

（3）（F，K）—— 父亲正常，母亲色盲；

（4）（S，Z）—— 父亲色盲，母亲正常；

（5）（S，C）—— 父亲色盲，母亲次正常；

（6）（S，K）—— 父母亲均色盲.

以下来分析各类夫妇的后代子女中色盲所占比例.

第一类，显然子女中没有色盲.

第二类夫妇（F，C）的子女情况如下表：

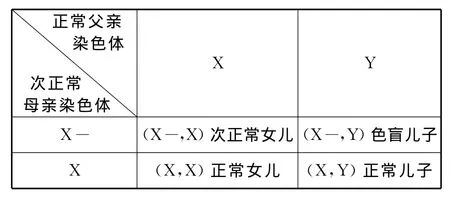
四种情况子女染色体配对中，仅有一类是色盲，占子女人数的1／4.故在子代总人口中的比例为2pq2／4＝pq2／2.

依次计算其他四类夫妇子女中色盲所占比例，分别为p2q／2、0、p2q和p3.

注意到p＋q＝1，合起来，子代中色盲所占的比例为：

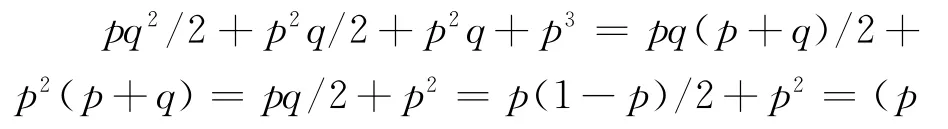
到此.我们惊讶地发现：原来子代中的色盲比例，与父母那一代色盲比例完全一样，没有升高的迹象.于是大家都松了一口气！大家不必担心因为遗传原因人类全都成为色盲.这是绝对不会的.

数学家用其数学智慧和数学方法，彻底解决了这个大难题.数学的力量真够神奇！

文化数学的建设，是一个巨大、系统工程.以上只是窥豹之一斑.但只要我们努力去想，努力去做，坚持不懈，从低年级数学课程做起，从小学一年级数学做起，一步步，积少成多，把学校数学课程进行文化包装，相信是一定会成功的.