用试探方程法求解Boussinesq方程
杨玉婷,崔泽建
(西华师范大学数学与信息学院,四川 南充 637002)
非线性发展方程已广泛应用于自然科学的各个领域,而求解非线性发展方程[1]的精确显示解又是至关重要的.至今已经发展了一些有效的方法,包括逆散射法[2]、Backlund 变换[2]、双线性法、对称性法[3]等.本文利用由刘成仕提出的试探方程法[4-7]结合积分变换求解一个重要的非线性发展方程——Boussinesq方程,得到了方程的3类精确显示解.
1 试探方程法
我们考虑偏微分方程
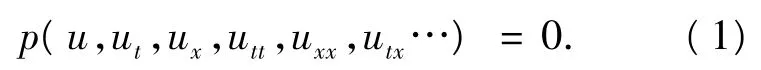
这里p是一个多项式,我们首先做一个行波变换
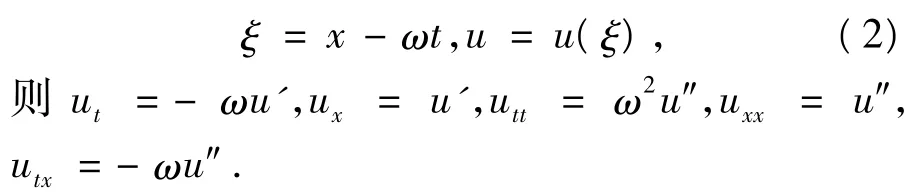
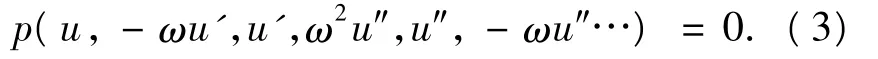
有时通过积分可以对方程(3)进行降阶.试探方程法可以概述为以下几个步骤:
第1步 采取如下多项式变换
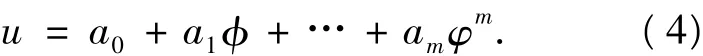
其中,φ是ξ的一个未知函数,这里a0,a1,…,am为确定的常数,且m≥1.
这样方程(3)可以变成
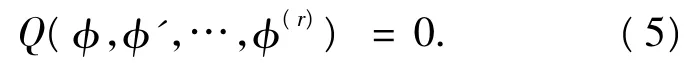
Q为相应的多项式.
第2步 我们令
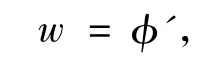
则
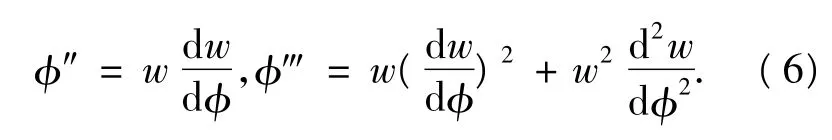
把(6)代入方程(5)可得
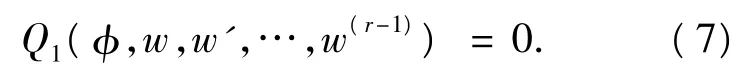
第3步 假设方程(7)有如下多项式形式的解:

这里,b0,b1,…,bn是确定的常数.利用齐次平衡原理可以得到m和n的关系,把试探多项式(8)代入(7)可以得到一个关于φ的多项式,再根据多项式的系数相等可以得到一个代数方程组,然后通过解这个代数方程组,就可以得出a0,a1,…,am,b0,b1,…,bn的值.
第4步 积分以下一阶常微分方程
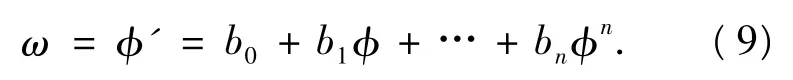
我们可以得到φ的值,进一步我们可以通过把φ的值代入方程(4)得到u的值.
2 应用
下面我们通过用试探方程法来求解Bouss-inesq方程:
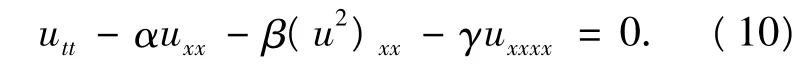
其中 α,β,γ 为常数.
先进行行波变换,然后再积分,Boussinesq方程变为如下形式
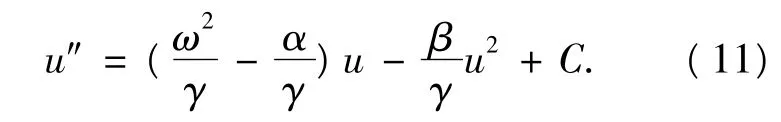
这里,C是任意的常数.为了求解的方便,不妨设
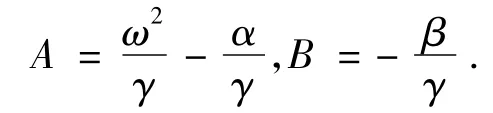
根据我们上面所述的试探方程法,结合齐次平衡原理,我们可以得到
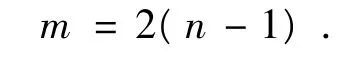
首先取 m=2,n=2 ,则
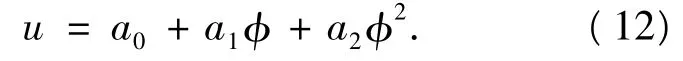
把(12)式代入(11)式可以得到
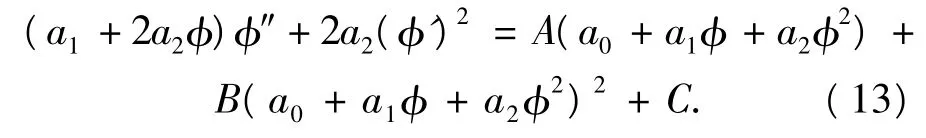
根据变换(6)式、(13)式可以变成如下一阶常微分方程:
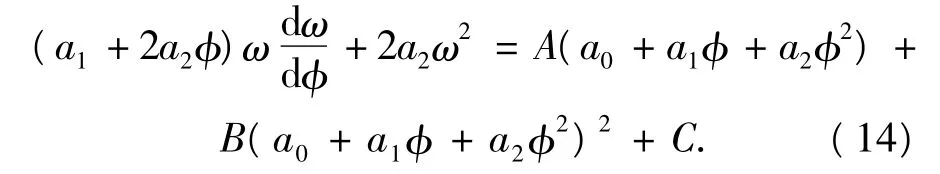
进一步,我们假设(14)具有如下多项式形式的解
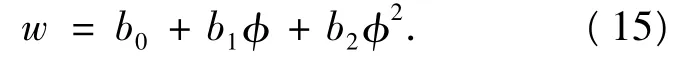
把表达式(14)代入(13)可以产生一个关于φ的多项式.令多项式的系数为零,可以得到如下代数方程组:
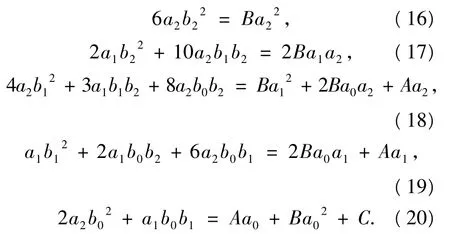
解这个代数方程组得到一族参数的值
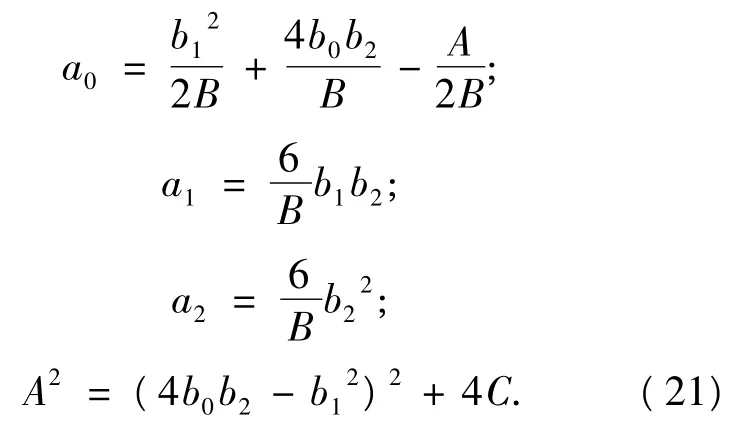
不失一般性,我们可以取b1=0,对b0,b2分别取不同的值.
1)若b0=1,b2=-1,则φ =coth(ξ-ξ0),所以
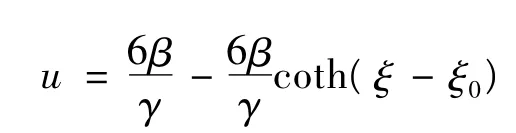
或
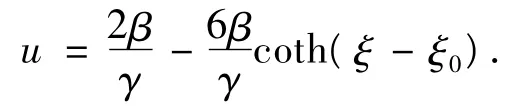
2)若 b0=-1,b2=1,则φ =tanh(ξ-ξ0),所以
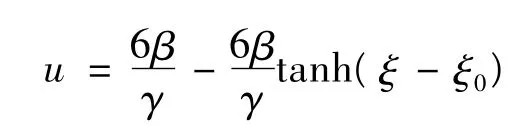
或
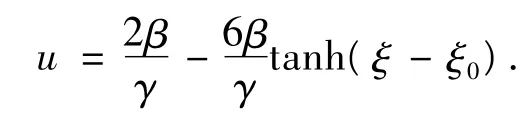
3)若b0=1,b2=1,则 φ =tan(ξ- ξ0),所以
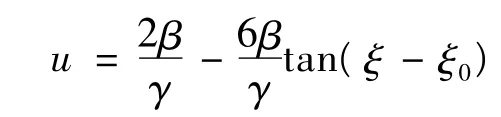
或
现在,我们再取m=4,n=3,不失一般性,设
于是可以得到相应的代数方程组
解得:
不失一般性,取b1=1,则
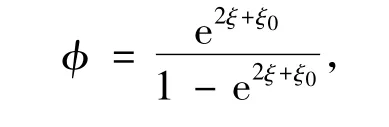
所以

3 结语
本文利用试验方程法求解了Boussinesq方程,得到了3种形式的精确解,即正切函数形式、双曲函数形式和指数形式.从求解Boussinesq方程的精确显示解的过程来看,试探方程法是简捷、方便、切实可行的,它丰富了Boussinesq方程的解系.此外,这些解对于解释一些物理现象也是很有帮助的,期待这种方法在求解其他非线性发展方程中发挥更大的作用.
[1]Du Xinghua.An irrational trial equation method and its applications[J].Pramana-J.Phys.,2010(73):415-422.
[2]Wang Dengshan,Li Hongbo.Single and multi-solitary wave solutions to a class of nonlinear evolution equations[J].J.Math.Anal.Appl.,2008,343:273-298.
[3]李志斌.非线性数学物理方程的行波解[M].北京:科学出版社,2007:11-21,57-92.
[4]Liu Chengshi.Trial equation method based on symmetry and applications to nonlinear equations arising in mathematical physics[J].Found Phys.2011,41:793-804.
[5]Liu Chengshi.All single traveling wave solutions to Nizhnok-Novikov-Veselov equation[J].Commun.Theor.Phys.2006,45:991-992.
[6]Liu Chengshi.The representation and classification of all single traveling wave solutions to sinh-Gordon equation[J].Commun.Theor.Phys.2008,49:153-158.
[7]Liu Chengshi.New trial equation methods and exact solutions to some nonlinear mathematics physical equations[J].Far East J.Appl.Math.2010:40,49-64.

