基于第二类椭圆积分的子午线弧长反解新方法*

过家春

(1)安徽农业大学理学院，合肥 230036 2)江西省数字国土重点实验室，抚州344000)

基于第二类椭圆积分的子午线弧长反解新方法*

过家春1，2)

(1)安徽农业大学理学院，合肥 230036 2)江西省数字国土重点实验室，抚州344000)

基于第二类椭圆积分及拉格朗日反演理论，推导出子午线弧长反解的新方法。该方法为归化纬度的余弦函数的泰勒级数展开，给出了子午线弧长的分析解。算例表明，其收敛速度快，精度可靠，可以满足实际应用精度要求。

子午线弧长反解;第二类椭圆积分;拉格朗日反演;泰勒级数;超几何函数

1 引言

子午线弧长反解问题(图1)是大地测量学、地图学等学科领域中的基础性问题。国内外关于这一问题的计算方法主要分为4种类型［1-4］，文献［1］进行了系统分析。当前我国所采用的解法主要有牛顿迭代算法、基于三角级数回代理论的直接算法两种［4］，主要用于求解高斯投影坐标反算中的底点纬度［4，5］。已有学者指出这一问题的算法仍然不够简洁，没得到完美的解决［6，7］。近年来，子午线弧长反解的递归算法、Hermite插值方法、幂级数展开方法等［6-8］被提出。其中，文献［6］及［7］中的级数展开方法开辟了子午线弧长反解的新思路。笔者在文献［9］中将子午线弧长公式变换为第二类椭圆积分的标准形式，并指出子午线弧长反解的本质实为第二类椭圆积分的逆。本文将以此为基础，引入拉格朗日反演理论，给出子午线弧长反解的新方法。

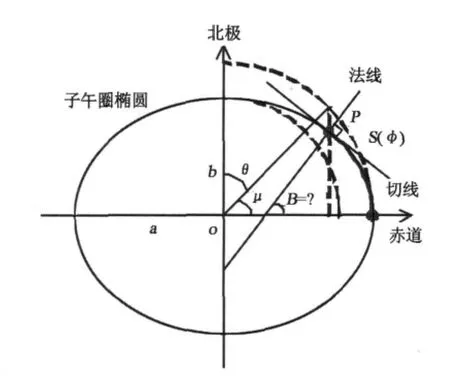
图1 子午线弧长反解Fig.1 Inverse solution of the Meridian

2 理论基础

2.1 子午线弧长与第二类椭圆积分之间的关系

在文献［9］中，已经得到:

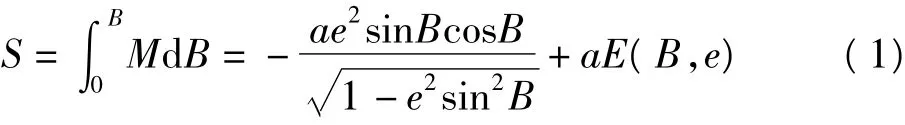
式中，

为第二类不完全椭圆积分。特别地，当大地纬度B =90°时，四分之一椭球子午线弧长为

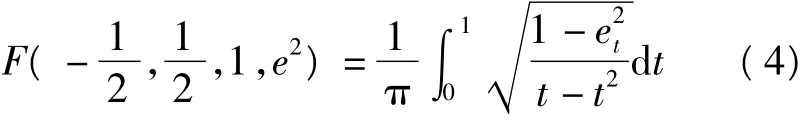
为书写方便，本文以下简记为F。顺便指出，按二项式定理展开计算子午线弧长公式中的首项常系数A与F之间的关系为

若以归化纬度μ为积分变量，则有

式中，θ为归化纬度的余角，即θ=π/2-μ。特别地，当μ=90°时，亦得式(3)。其中大地纬度B与归化纬度μ之间的关系为

2.2 拉格朗日反演定理(Lagrange Inversion Theorem)［10-12］

若函数y=f(x)在点x0的某一邻域U(x0)内可展开为泰勒级数

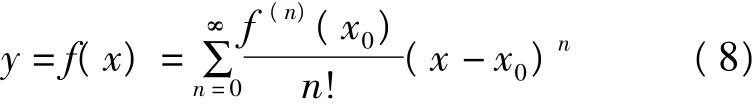
且f'≠0，则其反函数x=f-1(y)在相应的y0点的某一邻域V(y0)内也可展开为泰勒级数

式中，记y0=f(x0)=f(0)(x0)。进一步地，对于在邻域U(x0)内无穷可微的函数g(x)，也有

拉格朗日反演定理表明，在一阶导不等于零的情况下，解析函数的反函数也可展开为泰勒级数。以下讨论将以此为重要理论基础。

3 基于第二椭圆积分的子午线弧长反解公式推导

以式(6)为基础，定义

这样，子午线弧长反解问题即转换为了第二类椭圆积分的求逆问题。

并构造函数

这里，视函数f(x)是以θ、β为中间变量，以t为自变量的复合函数。易得

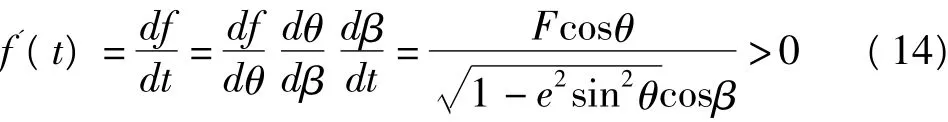
由于第二类椭圆积分E(θ，e)在θ=0处可展开为泰勒级数，根据拉格朗日反演定理，函数(12)在t =0也可展开为泰勒级数

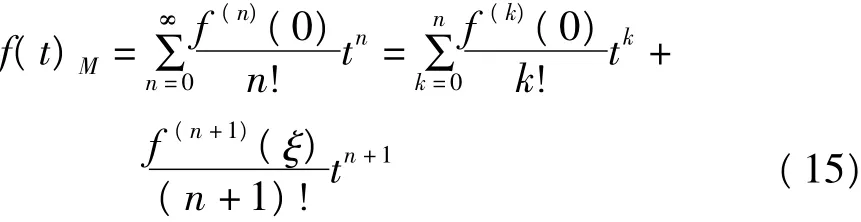
式中，记f(0)(0)=f(0)。根据泰勒中值定理，该级数是收敛的，ξ是0与1之间的某个值。这里记f (t)的级数展开式为f(t)M，以区分式(13)。

由复合函数求导法则，对于二阶及二阶以上导数有:

不难发现，各阶导数中的偶数阶导数均含有sinθ及sinβ因子，所以在t=0处有

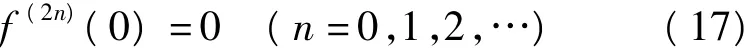
此处记f(0)(0)=f(0)。由此，式(15)可化简为

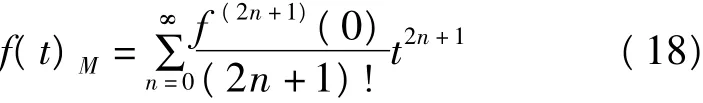
上式二阶以上导数的手工求解是比较困难的，笔者在计算机代数系统Maple中求得其前11阶导数在点t=0处的值分别为

据此，可取近似值

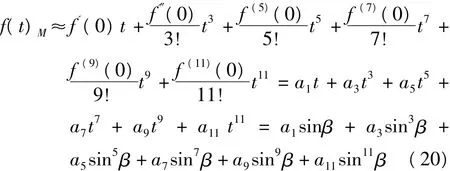
因此可得

上式要求f(t)M≠0。显然，当 f(t)M→0时，Bf→90°。实际上，当S=S90°时也不必用此式反解。这里，反算结果记为μf及Bf，以区分正算，Bf亦对应于高斯投影坐标反算中的底点纬度。实际应用时，还可以根据精度需要，求出更高阶导数。

另外，式(19)的系数是有规律可循的，其包含两个整数数列:

1)特别地，当e=0时，式(19)即化为sin［Farcsin(θ/F)］的麦克劳林级数展开式的奇数阶导数值，其系数规律参见整数数列线上大全A008956［13］，即为式(19)的外部系数。

2)若上述讨论中不再令t=sinβ，而将f(β)= sinθ视为以β为自变量的复合函数，则其麦克劳林展开式为

顾及大地纬度B与归化纬度μ之间的关系(6)，易得

求至11阶的导数值为

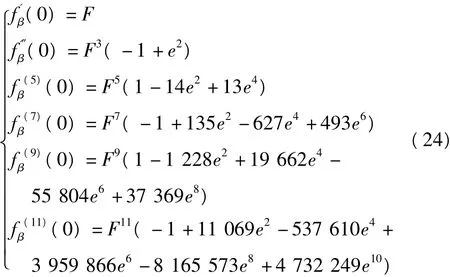
经验证，式(23)与式(18)比较，其收敛速度较慢，但其系数结构为式(19)的内部系数。该系数涉及第二类椭圆积分，其规律需进一步研究。

4 算例与分析

对于特定的地球椭球，以上给出的基于第二类椭圆积分的子午线弧长正反解公式中的E、F及式(18)的系数为涉及椭球第一偏心率e及相应超几何函数F的常数。在此，首先将我国几个常用地球椭球正反解所涉及到的一些常量，及式(18)的系数列于表1。为便于误差分析，表中小数点后取位较多(末位采用四舍五入法)，在实际应用时可根据精度需要对表中各参数数位进行适当取舍。

表1数据显示，各种椭球下该级数的收敛速度都很快。以我国CGCS2000椭球为例进行反算验证，计算结果列于表2，f(t)M、μf及Bf的误差曲线如图2所示。

表2及图2表明，式(18)收敛速度很快，反算大地纬度的误差ΔB依赖于Δf，随纬度增大而减小，呈非线性变化。在实际测量工作中，一般要求通过公式的解算精度应高于观测精度。按这样的原则，大地纬度的解算精度应不低于3.3×10-6″，即对应的子午线弧长精度不低于0.1 mm。经计算分析，在纬度大于15°的地区，将级数展开至9阶导的纬度解算误差在2.2×10-6″以内;在纬度大于1°的地区，将级数展开至11阶导，误差在4.42×10-7″以内。在我国地理纬度范围，展开至11阶导即能满足实际应用要求，在纬度大于15°的地区展开至9阶导即可。

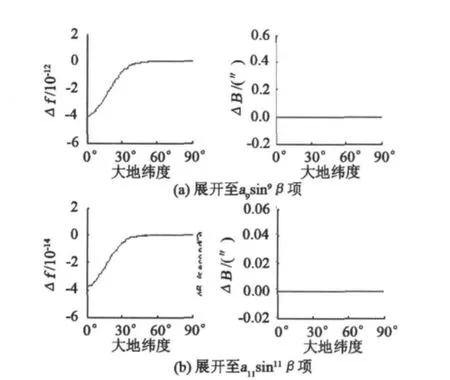
图2 子午线弧长反解新方法误差曲线Fig.2 Error curves of the inverse solution of the Meridian Arc Length with the new methods

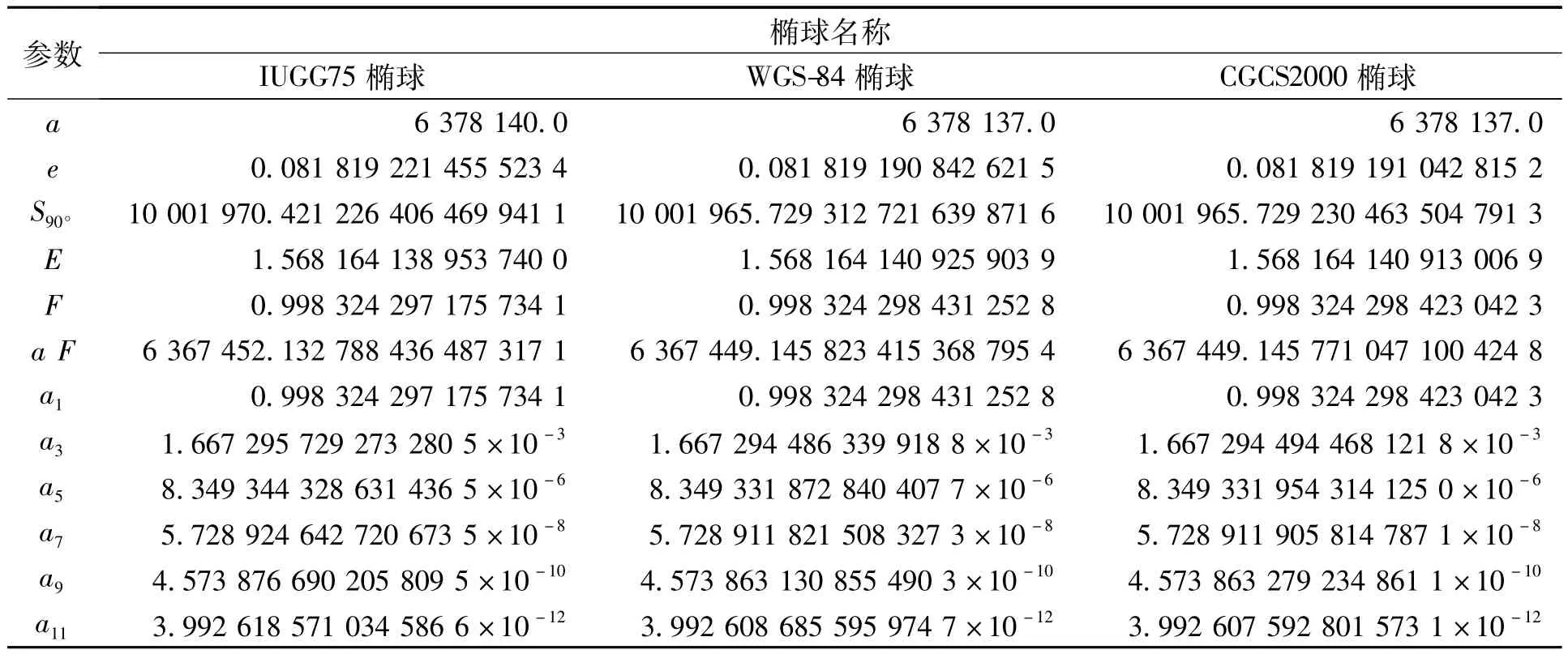
表1 涉及第二类椭圆积分的常用地球椭球的一些常量Tab.1 Several constants of different ellipsoids related to the Elliptic Integral of the Second Kind

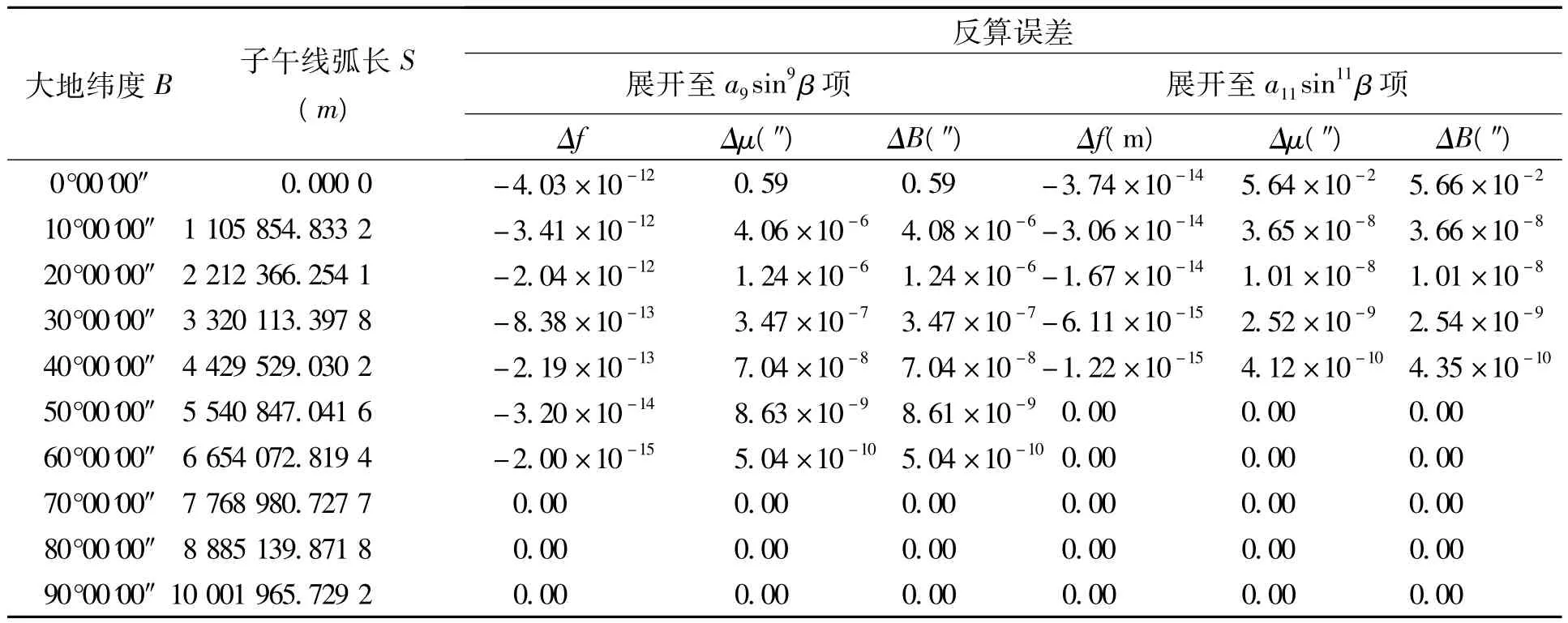
表2 基于第二类椭圆积分的子午线弧长反解新方法例证表Tab.2 Illustration of the new method for inverse solution of Meridian by Elliptic Integral of the Second Kind

在赤道附近，需展开至更高阶项方能达到上述精度要求，公式较为冗长，解决的途径是可按本文方法在β=π/2处展开为泰勒级数，此不赘述。

与现有的方法对比，本文的反解方法的特点主要体现在:

1)提供了一种新的子午线弧长反解直接算法，相对于传统的3种直接算法精度有明显提高:基于三角级数回代理论的直接算法、Helmert公式直接算法及表达为子午线弧长S的多项式逼近算法的最弱精度分别约 1.3×10-5″、2.0×10-5″及 1.0× 10-4″［1，4］，本文算法精度如前所述，且可通过将级数展开至更高阶项，以达到任意精度的结算。

2)高斯超几何函数的引入对子午线弧长正反解理论的完善具有一定的推动作用。首先，如式(5)所示，该参数出现在子午线弧长的正解中。而在反解中，除在本文出现外，经典的迭代算法及直接算法的初值实际为S/aF，也涉及该参数。在其他大地测量问题中，该参数是否仍会出现，需进一步研究。

3)新方法还主要体现在其分析特点。已有的直接算法、迭代算法、插值方法、高斯-勒让德求积法等方法均属于数值计算方法的范畴，事实上仍有许多其他的数值近似解方法可以用于子午线弧长的反解计算，能够满足实际应用的精度要求。而本文方法为纬度函数的常系数、收敛的幂级数展开，可以根据精度需要任意展开，可扩展性好。该方法属于数学分析范畴，给出了子午线弧长反解的分析解，是对已有方法的补充，并有助于研究子午线弧长的函数规律。

5 结语

本文基于勒让德第二类椭圆积分，利用拉格朗日反演定理，将子午线弧长反解问题转换为第二类椭圆积分的求逆问题，得到子午线弧长反解的泰勒级数展开新方法，精度可靠，可以满足实际应用的精度要求。

1 朱华统.底点纬度计算方法评述［J］.测绘通报，1978，5: 10-14.(Zhu Huatong.Review on the methods for calculating latitude of low points［J］.Bulletin of Surveying Mapping，1978，5:10-14)

2 Wolfgang Torge.Geodesy(3rd.)［M］.Berlin:Walter De Gruyter，2001:91-98.

3 Deakin R E and Hunter M N.Geometric geodesy part A［M］.Melbourne:School of Mathematical and Geospatial Sciences，RMIT University，2010:60-77.

4 孔祥元，郭际明，刘宗泉.大地测量学基础［M］.武汉:武汉大学出版社，2001，64-73.(Kong Xiangyuan，Guo Jiming and Liu Zongquan.Foundation of geodesy［M］.Wuhan:Wuhan University Press，2001:64-73)

5 丁佳波.利用底点纬度进行高斯投影换代计算［J］.测绘学报，1993，22(3):212-217.(Ding Jiabo.The transforming the zones of Gauss projection from latitudes of low points［J］.Acta Geodaetica et Cartographica Sinica，1993，22(3):212-217)

6 易维勇，边少峰，朱汉泉.子午线弧长的解析型幂级数确定［J］.测绘学院学报，2000，17(3):167-171.(Yi Weiyong，Bian Shaofeng and Zhu Hanquan.Determination of foot point latitude by analytic positive serires［J］.Journal of Institute of Surveying Mapping，2000，17(3):167-171)

7 Shaofeng Bian and Yongbing Chen.Solving an inverse problem of a meridian arc in terms of computer Algebra system［J］.Journal of Surveying Engineering，2006，132(1):7-10.

8 施一民，范业明.一种子午线正反解算的新方法［J］.同济大学学报(自然科学版)，2005，33(7):964-966.(Shi Yimin，and Fan Yeming.New method for direct and inverse solution of meridian［J］.Journal of Tongji University(Nature Science)，2005，33(7):964-966)

9 过家春，等.基于第二类椭圆积分的子午线弧长公式变换及解算［J］.大地测量与地球动力学，2011，(4):94-98.(Guo Jiachun，et al.Calculating meridian arc length by transforming its formulae into elliptic integral of the second kind［J］.Journal of Geodesy and Geodynamics，2011，(4):94-98)

10 Abramowitz M and Stegun I A.Handbook of mathematical functions with formulas，graphs，and mathematical tables［M］.Dover Publications，INC.，New York，1972.

11 http://en.wikipedia.org/wiki/Lagrange_inversion_theorem.

12 Ferraro G.Lagrange inversion theorem:The rise and development of the theory of series up to the early 1820s［M］.Springer，New York，2008.

13 Sloane N J A.The on-line Encyclopedia of Integer Sequence:http://oeis.org/A008956.

NEW METHOD FOR INVERSE SOLUTION OF MERIDIAN BASED ON ELLIPTIC INTEGRAL OF SECOND KIND

Guo Jiachun1，2)

(1)School of Science，Anhui Agricultural University，Hefei 230036 2)Jiangxi Province Key Lab.for Digital Land，Fuzhou344000)

According to the theory of the elliptic integral of the second kind and Lagrange inversion theorem，we present a new method to solve the inverse problem of Meridian arc length，which is expressed by Taylor Series generated from the cosine function of reduced latitude.It gives a analytical solution for this problem.Numerical calculations are used to illustrate the accuracy of the method and the results show that it is applicable and useful in practice.

inverse solution of meridian;elliptic integrals of the second kind;Lagrange inversion theorem;Taylor series;hypergeometric function

1671-5942(2012)03-0116-05

2011-12-25

江西省数字国土重点实验室开放研究基金资助项目(DLLJ201211);国家农业信息化工程技术研究中心开放课题(KF2010W40-046)

过家春，男，1981年生，硕士，讲师，主要研究方向为大地测量学、地图学与地理信息系统.E-mail:guojiachun@ahau.edu.cn

P226

A