基于分数跳扩散过程的幂期权定价

胡素敏,胡电喜

(1.河南城建学院数理系，中国 平顶山 467036；2.玉溪师范学院商学院，中国 玉溪 653100)

期权定价问题一直是金融数学和金融工程学研究的核心问题之一.在以往的期权定价中,人们普遍假设标的资产价格服从几何布朗运动,它是一个连续的随机过程,而在金融市场上,一些重要信息的到达会刺激股票价格发生不连续的跳跃,因此股票价格应包含连续扩散过程和不连续的跳跃过程两方面,在几何布朗运动下,资产价格变化是相互独立的随机变量,资产收益率服从正态分布,而近年来对股票市场的大量研究表明股价变化不是随机游走,而是呈现不同程度的长期相关性,分数布朗运动[1]恰好具有这些优点,因此用分数布朗运动刻画资产价格的变化,更符合实际情况.

自引入分数布朗运动以来,国内外出现了大量的相关研究.Ciprian[2]研究了分数布朗运动环境下的期权定价. Rogers[3]研究了分数布朗运动下的套期保值,周圣武[4]研究了分数布朗运动环境下的幂期权定价.欧辉[5]研究了债券价格随机时重设型熊市认售权证的定价,刘韶跃[6]研究了分数布朗运动环境中混合期权定价.本文基于风险中性等价鞅测度,推导出标的股价服从分数跳扩散过程的幂期权的看涨、看跌及平价公式,并得出相关推论.

1 股票价格的分数跳扩散行为

股票价格受到市场重要信息刺激时,会呈现不连续的跳跃行为,本文对股票价格作如下假设：

(H1) 股票价格ST遵循It过程[7]

(1)

其中r是无风险利率,σ是股价的波动率，λ(λ>0)是跳跃强度,表示一年中股票价格的平均跳跃次数,qt是一个强度为λ的Poisson计数过程[8-9],dqt是描述St发生跳的点过程,当股票价格发生跳跃时dqt=1,否则dqt=0；k=E(U),BH(t)为分数布朗运动.应用It公式解随机微分方程(1),可得股票价格的对数过程lnSt所满足的常系数随机微分方程

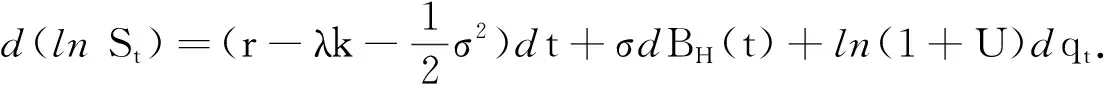
(2)

解随机微分方程(2),并应用Poisson过程的性质,可得时刻股票价格的表达式

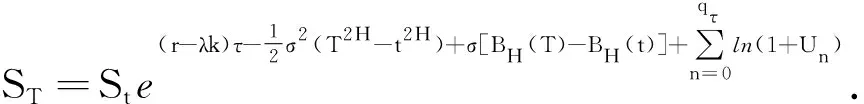
(3)

(4)

其中Un表示股票价格在第n个跳跃时刻tn的跳跃幅度,并假设U1,U2,…，Un,…是一列独立同分布的随机变量.应用全期望公式可得股票价格在T时刻的数学期望. 为表述方便,本文将沿用Merton[10]的假设：

(H2) 假设U,qτ,BH(t)相互独立,且1+U服从对数正态分布,即

(5)

其中μ,σU为常数.

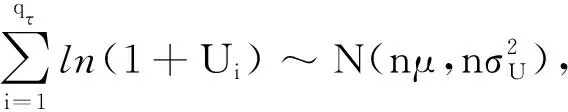
(6)

而且由U,qτ,BH(t)相互独立可知Z1,Z2也相互独立.

由(4)和(6)以及正态分布的可加性可知,当qτ=n时,存在标准正态随机变量Zn～N(0,1),使得

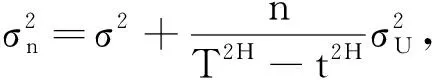
(7)

2 欧式幂期权的定价

在风险中性世界里,欧式看涨幂期权到期日的期望价值为

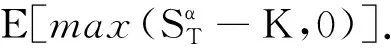
(8)

根据风险中性定价原理,看涨幂期权的价值是(8)以无风险利率贴现的现值,即

(9)

定理1标的股票价格St服从分数跳扩散过程(1)、执行价格为K的欧式看涨幂期权在t时刻的价值为

(10)

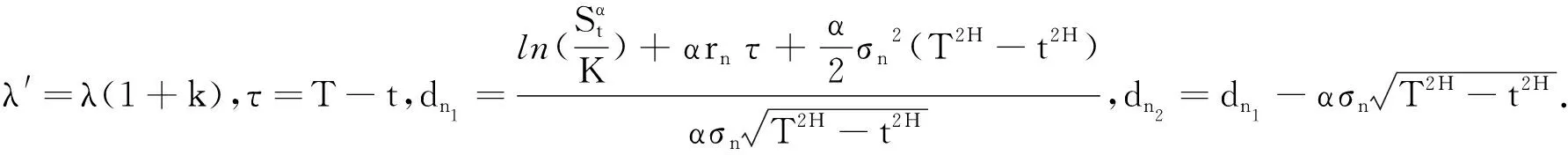
证由(9)得

(11)

第1个数学期望为

(12)

第2个数学期望为

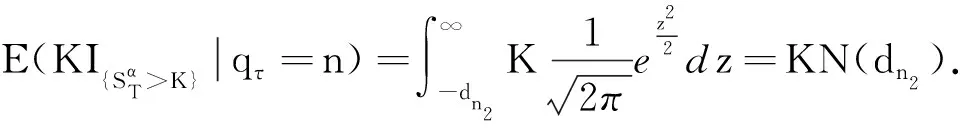
(13)

将(12)、(13)式代入(11)式得

(14)

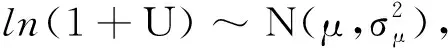
(15)

将(15)式代入(14)式得

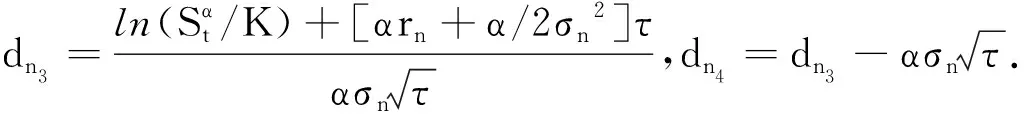
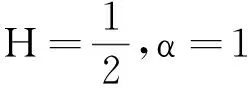
此定价公式与文献[12]结论相同.

Ct=StN(d1)-Ke-rrN(d2).

定理2标的股票价格St服从分数跳扩散过程(1)、具有相同执行价格K的欧式看涨幂期权与看跌幂期权在t时刻的平价公式为

(16)

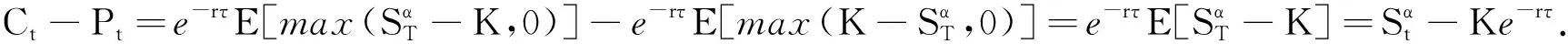
定理3标的股票价格St服从分数跳扩散过程(1)、执行价格为K的欧式看跌幂期权在t时刻的价值为

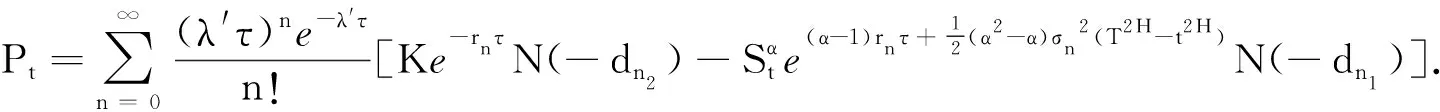
证由(16)式可得

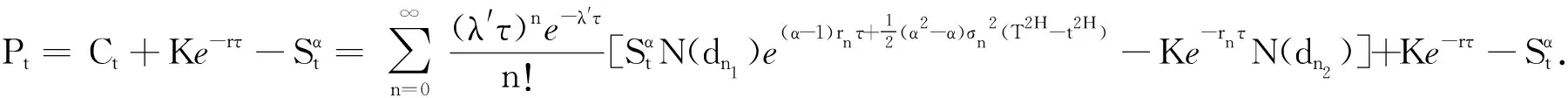
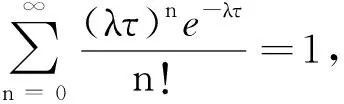
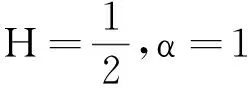
此定价公式与文献[12]的结论相同.

Pt=e-rτKN(-d2)-StN(-d1).

参考文献：

[1] 谢和平.分形应用中的数学基础与方法[M].北京:科学出版社, 1997.

[2] CIPRIAN N. Option pricing in a fraction Brownian motion environment[J].Pures Math, 2002,2(1):63-68.

[3] ROGERS L C G. Arbitage with fractional Brownian motion[J]. Math Finance, 1997,7(1):95-105.

[4] 周圣武.分数布朗运动环境下的幂期权定价[J].大学数学, 2009,25(5):69-72.

[5] 欧 辉.债券价格随机时重设型熊市认售权证的定价[J].湖南师范大学自然科学学报, 2011,34(6):16-20.

[6] 刘韶跃.分数布朗运动环境中混合期权定价[J].工程数学学报, 2006,23(1):153-157

[7] 黄志远.随机分析学基础[M].北京:科学出版社, 2001.

[8] 陈良均,朱庆棠.随机过程及其应用[M].北京:高等教育出版社, 2003.

[9] 张 波,张景肖.应用随机过程[M].北京:清华大学出版社, 2006.

[10] MERTON R C. Option pricing when underlying stock returns are discontinuous[J]. J Financial Econ, 1976(3):125-144.

[11] 周圣武,周长新,李金玉.概率论与数理统计[M].北京:煤炭工业出版社, 2007.

[12] 姜礼尚.金融衍生产品定价的数学模型与案例分析[M].北京:高等教育出版社, 2008.

[13] BLACK F, SCHOLES M. The pricing of options and corporate liabilities[J]. J Political Econ, 1973,81(2):637-659.