基于极点配置的改进晕轨道控制方法

晁宁 罗晓英 李言俊

（1西北工业大学航天学院，西安710072）（2西安电力电子技术研究所，西安710061）

1 引言

由于地月系平动点附近的指数不稳定性，且系统模型建立不完备、不准确以及入轨误差执行偏差等因素，航天器在其上晕轨道运行时进行轨道控制是必不可少的；而自从开始了各种平动点空间任务，晕轨道保持控制就一直是研究的热点。轨控精度是测控精度、执行精度、扰动等诸多因素的多元函数，由于控制级数的长足发展及执行元件工艺的提升，目前轨控精度最高可达米的量级。文献［1-2］最早提出了target控制模式，文献［3］同样基于线性化模型的思想，给出了控制器精度与能耗均满足要求的折中策略。文献［4］提出了一种线性二次型最优LQR控制方法来保持晕轨道的稳定，所设计的线性控制器也可以用于确定Halo轨道。文献［5］利用最优控制理论中极值曲线的变分成功求解了两点边值问题，实现了Halo轨道维持。考虑到最优控制求解的难度，文献［6］提出了用于近似求解HJB方程的θ-D方法，这种方法具有很高的实时性。文献［7］将序优化理论与微分修正法相结合，优化了晕轨道的入轨机动问题。这种方法在优化过程中具有收敛速度快、对初值不敏感与计算量小的优点。

本文对无摄三体动力学方程沿标称轨道线性化，推导了三体动力模型的误差线性模型。在线性模型的基础上，利用模型标准轨道状态向量选择闭环目标极点，通过设计闭环极点配置控制状态反馈增益阵K对地月系L1点附近受摄晕轨道进行了控制仿真与对比。针对K中三通道使用单一控制量级带来的控制误差，提出了利用入轨误差比例设计的可变反馈阵系数 （VKC）设计方法。根据入轨误差在三轴分量上的不同比例来确定对三轴控制力度的大小，对入轨误差的变化具有一定鲁棒性。

2 圆限制性三体模型

对于圆限制性三体问题 （Circular Restricted Three-Body Problem，CRTBP），可描述为一个质量忽略不计的小天体P在两个相互环绕运动的大天体P1、P2（P1＞P2）引力作用下的运动状态，通常利用以两大天体质心为圆心旋转的会合坐标系（或称旋转坐标系）来研究，这是比二体问题更精确的一种合理近似。假定P不影响P1、P2的运动，两大天体共同绕其质心做角速度为ω的圆周运动。P1指向P2的方向为会合坐标系的x轴，ω方向为z轴，y轴与x、z轴成右手系。这种假设下的动力学模型不考虑摄动因素，即无摄圆限制性三体模型，小天体的无量纲化运动对应一个二阶常微初值问题，其分量形式为

对于该CRTBP目前仅找到5个特解和一个Jaccobi积分［8］。前者对应5个引力平衡点，即作用在旋转坐标系中这5个点上的航天器的引力和离心力相平衡，其中3个共线平衡点不稳定，位于两大天体连线上，记作Li（i＝1，2，3）；两个三角平衡点Lyapunov稳定。由于前两个点的应用价值较大，引发了学者们的深入研究。5个平衡点处对应的Jacobi积分常数Ci（μ）有如下关系：

曲面2Ω（x，y，z）＝C即为零速度面［8］。

3 晕轨道特性及线性化

（1）晕轨道特性

晕轨道是存在于共线平动点附近的一类周期轨道。这种轨道具有许多特殊的动力学特性，主要有不稳定性、周期性及可控性，并且对初始值十分敏感，详见文献［9］。以晕轨道周期Thalo＝13.580 8天，入轨精度为10-8（10m）量级为例，由于其不稳定性，运行于地月系L1点晕轨道上的无控航天器最多在维持约3个周期后就开始发散，如图1所示。轨道初值为

图1 地月系L1点某晕轨道Fig.1 Earth-Moon system L1point some halo orbit

本文将以图1中晕轨道的第一周期作为标准轨道，并人为引入不同等级的误差进行极点配置控制分析。

（2）线性化

由于深空探测的无摄圆限制性三体模型表现出很强的非线性，在考虑摄动因素后这种非线性特性就更加明显。而在一定时间范围内，当实际轨道与标准轨道的状态误差较小时，其误差系统模型具有较强的线性特性。误差线性系统模型具有较高的准确度。通常用到的线性化方法有两种：

1）将误差状态作为新的状态变量，利用多元向量函数的雅可比矩阵作为线性系统的系数矩阵；

2）仍以原位置速度作为状态量，将动力学系统转换关系作为系数矩阵。

以第一种方法为例，将误差状态作为新的状态变量，利用多元向量函数的雅可比矩阵作为线性系统的系数矩阵A。设状态变量控制向量u＝［uxuyuz］T，晕轨道标准状态为状态误差则非线性系统可近似化为线性系统［9］

式中b1＝0。方便起见，下面均用X代替Z。

4 极点配置方法

对于近似小偏差线性系统来说˙X＝AX＋Bu，X为误差向量。如果控制起始点存在一个状态偏差，则动力学系统存在两种线性化基础，即沿理论轨道线性化或沿实际轨道线性化。两种基础对应理论系数矩阵Am（t）与实际系数矩阵Ap（t）。这样一来，如果基于实际轨道的线性系统完全能控，就可以利用状态反馈矩阵K，以Am（t）为目标对Ap（t）进行极点配置。

（1）基于误差线性系统的极点配置

一个线性定常系统的极点配置条件如下［10］：

设线性受控系统状态方程为

式中A∈Rn×n，B∈Rn×m，X∈Rn，u∈Rm，n为系统阶数，m为输入维数。若要通过状态反馈的方法使闭环系统极点配置于理想位置上，其充要条件是式（4）完全能控。

原开环系统˙X＝AX＋Bu通过加入状态反馈K∈Rm×n，构成闭环系统使系统镇定。系统结构如图2所示，双线代表多输入、多输出。图2中可见，闭环系统的动态方程变为˙X＝ （A-BK）X＋Bv，对受控系统进行极点配置的关键是求解状态反馈阵K。要利用状态反馈u＝v-Kx是闭环极点si（i＝1，2，…，n）位于指定位置λ1，…，λn，应满足

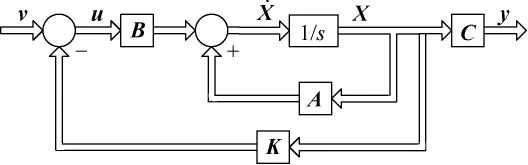
图2 状态反馈闭环结构Fig.2 Closed-loop of state feedback

本文受控模型主要为动态方程形式，状态反馈极点配置则是在误差线性模型的基础上进行。标准轨道初始值与真实轨道初始值在误差线性系统中将分别对应不同的系统矩阵Am和Ap。按照极点配置的思路，通过引入状态反馈增益阵K来实现近似线性系统镇定，则闭环系统的期望极点位于多项式det（sⅠ-Am）＝0的解在s平面上的位置。

根据误差线性系统的可加性，系统状态反馈阵K可以通过三轴分量叠加得到，即

另外由于控制律与三通道间偏差数量级的不同，反馈控制律在引入原非线性系统时存在比例系数ci（i＝1，2，3）以弥补原控制律三通道间单一数量级的缺陷。于是有反馈控制律u＝-KcX，其中状态向量

（2）可变反馈阵系数

试验发现，反馈增益阵K中常系数c1～c3的取值直接影响跟踪控制的精度。而误差级反映了飞行器在三通道上位置误差及速度误差的宏观情况，这种指标不能明确反映出三通道中各分量的误差大小。因此，若入轨误差主要由z通道引入，前面假设c1～c3的相互关系便不成立，这样同时也会给控制器引入设定误差。对于这种情况，本文考虑在系数设定阶段对状态偏差三分量所占比例进行分析，并按照各分量偏差比例自适应调整系数大小。

由式（8）能够看出K的系数与三轴偏差成正比，误差越大则控制幅度越大。进行数字仿真时，选取

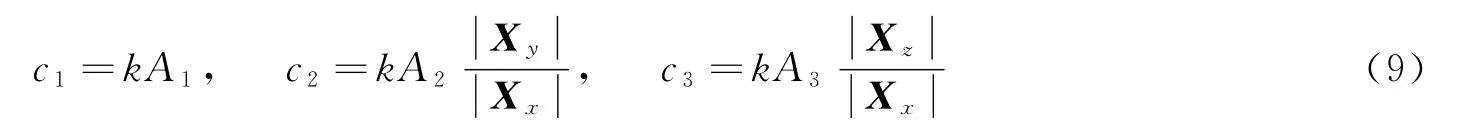
式中k为比例系数；A1～A3为幅值系数。幅值系数表示了三轴各自的数据跨度，跨度越大则控制幅度也越大。同样将比例系数完全归纳于k，则幅值系数取值为

比例系数k通过对跟踪方差和TVS寻优得到。

跟踪方差和 （TVS）表示三轴分量方差在控制周期T内的总和。TVS按照式（11）计算

式中为标准轨道状态；var为向量方差运算；Xcon为受控轨道状态；n为Thalo内的累加次数。

5 仿真试验

（1）固定系数反馈增益阵控制

利用地月系L1点晕轨道的小偏差线性模型和不同误差等级 （10-5～10-7）进行分析。选择˙X（0）＝0，y（0）＝0为晕轨道起点，幅值AX＝0.032 18。根据式（3）中的矩阵分块，系统的受控部分仅为A1子块，且该子系统能控。因此，仅对该部分子系统进行分析与控制是合理的简化计算。以误差等级为10-6，图1所示幅值晕轨道为例，表1列出了理论轨道与实际轨道分别对应的能控子系统矩阵元素。这里以对会合坐标系中x轴施控为例，选择控制矩阵b＝［1 0 0］T，则状态反馈阵k1＝［k1k2k3］T。

表1 子系统矩阵及极点位置Tab.1 Subsystem matrix and pole position

表1中，Am、Ap分别为A1在标准初始状态和实际初始状态下的取值。同理可得，坐标系中y轴与z轴两通道的状态反馈阵为

下面将通过误差线性系统推导出的反馈控制律引入原非线性系统中验证效果。以前述三维闭合halo周期轨道为控制对象，并根据式（7），系数关系选择为c1＝c2≈40c3。根据试验，误差在10-6数量级下取c1＝1／23.8，10-7数量级下取c1＝1／24.5，10-5数量级下取c1＝1／50。

图3是基于误差线性系统的控制情况。从中可见，3种误差等级下对应的控制效果不同，10-7误差级控制效果最好，受控轨道满足了闭合与周期性要求。对于周期halo轨道来说，如果选择单周期受控轨道首尾尽可能闭合为控制目标，则受控轨道入轨误差越小，受控轨道越接近理论轨道，跟踪控制效果越好。图3（c）表示的误差级最大，利用极点配置方法控制后，受控轨道虽在x-y平面内实现了周期轨道闭合，但在z方向仍存在不可消除的控制偏差。在实际轨道与理论轨道偏差较大时，利用线性系统的极点配置方法控制后并未获得一个闭合的周期轨道。这种情况也说明，对非线性动力学系统进行基于小偏差理论的误差线性化变换后得到的线性系统是对原三体动力学系统的近似，入轨误差越小，近似线性系统与原系统的相似度就越高。当入轨误差增大到一定程度时，基于近似线性系统推导出的控制律效果就会不理想。

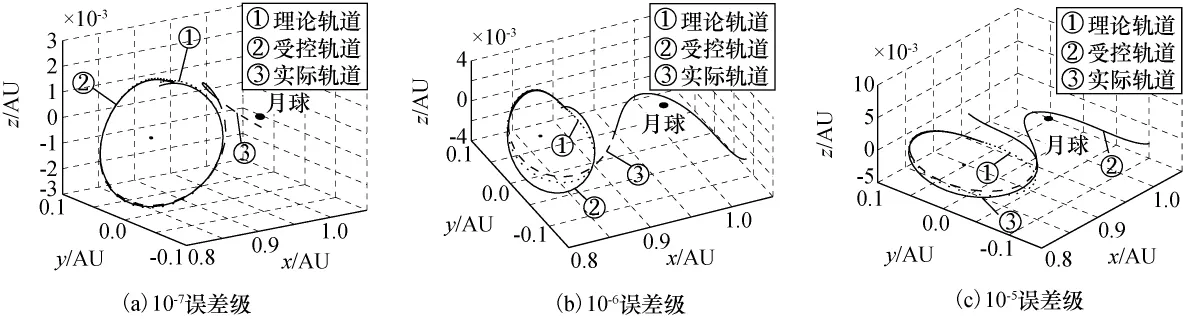
图3 极点配置前后控制情况Fig.3 Control effect of pole assigment

表2列出了3种误差级下的反馈增益阵常系数以及跟踪方差和TVS，TVS反映了受控跟踪轨道与理论轨道的接近程度，Ac表示控制过程中消耗的总加速度，为量纲一的变量。对比表2中的TVS值也能看出入轨误差小时跟踪精度较高，且消耗能量较少。

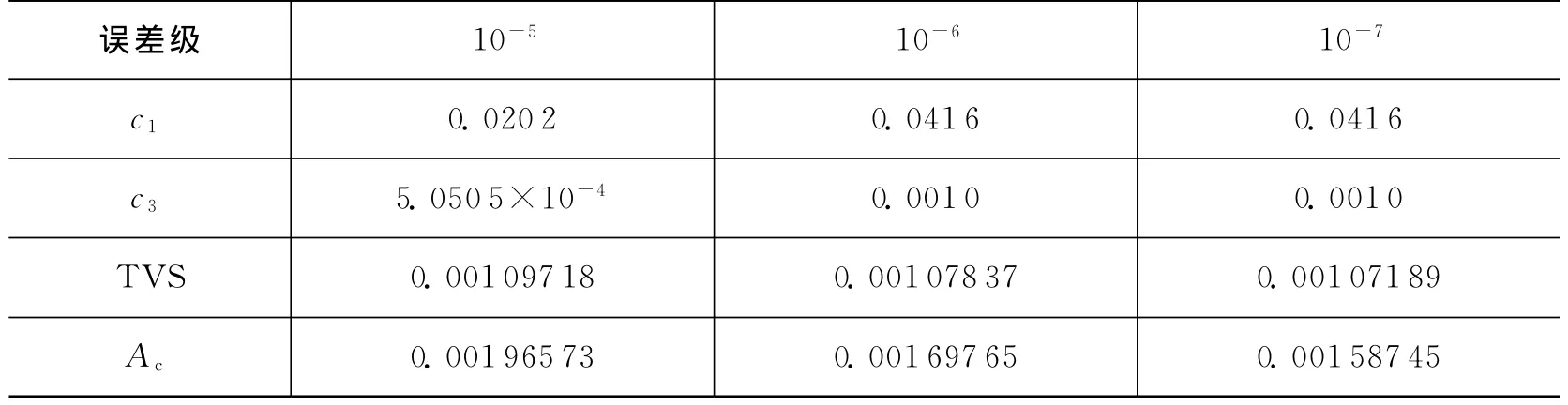
表2 不同误差级指标对比Tab.2 Comparison of performances in different error level

（2）VKC控制

采用可变反馈系数后的跟踪方差和TVSb对比如表3所示，TVSb中的下标 “b”表示可变系数控制方法。

表3 变系数方法控制效果Tab.3 Control effect of variable coefficient method

从表3中可以看到，采用变系数方法后的极点配置控制效果与固定系数法相比有所改善，各误差级下的跟踪方差和也相应减小。从图4中也可以看到使用改进方法后，即使在较大误差级别情况下也获得了闭合周期轨道，控制效果改善比较明显。但在较大初始误差情况下仍旧不能达到很高的控制精度，这主要是由于极点配置方法的固有缺陷带来的，如系统模型必须满足小偏差假设，基于状态空间方程推导的反馈控制律在原非线性系统下存在未建模动态等。实际非线性系统所需的控制量不一定与系统状态呈完全线性关系，这也是线性控制方法的固有缺陷。

6 结束语

本文利用闭环极点配置控制理论设计了状态反馈增益阵K，来实现对地月系L1点附近受摄晕轨道保持控制，并试验验证了可行性。针对K中三通道使用单一控制量级带来的控制误差，及误差线性模型对大入轨偏差的局限性，提出了利用入轨误差比例设计的VKC设计方法，区别对待各分量偏差，实现了对三轴的控制力度的自适应调整。改善了原有极点配置方法在较大入轨误差情况下受控轨道不闭合的情况，并通过仿真试验验证了控制效果。

［1］FARQUHAR R W.The Control and Use of Libration Point Satellite［R］.NASA TR R-346，1976.

［2］BREAKWELL J V，KAMEL A A，RATNER M J.Stationkeeping of atrans lunar communication station ［J］.Celestial Mechanics，1974，10（3）：357-373.

［3］HOWELL K C，PERNICKA J.Stationkeeping method for libration point trajectories ［J］.Journal of Guidance，Control and Dynamics，1993，16（1）：151-159.

［4］CIELASZYK D，WIE B.New approach to Halo orbit determination and control［J］.Journal of Guidance，Control and Dynamics，1996，19（2）：266-273.

［5］RAHMANI A，JALALI M A，POURTAKDOUST S H.Optimal approach to halo orbit control［C］.AIAA guidance，navigation，and control conference and exhibit，Austin，2003.

［6］XIN MING，DANCER M W.Station-keeping of an L2Libration point satellite withθ-D technique ［C］.The 2004American control conference，Boston，2004：1037-1042.

［7］胡少春，孙承启，刘一武.基于序优化理论的晕轨道转移轨道设计 ［J］.宇航学报，2010，31（3）：662-668.HU SHAOCHUN，SUN CHENGQI，LIU YIWU.Transfer Trajectory Design for Halo Orbit Based on Ordinal Optimization Theory ［J］.Journal of Astronautics，2010，31（3）：662-668.

［8］俞辉，宝音贺西，李俊峰.双三体系统不变流形拼接成的低成本探月轨道 ［J］.宇航学报，2007，28（3）：637-642.YU HUI，BAOYIN HEXI，LI JUNFENG.Low Energy Transfer to the Moon Using the Patching of Invariant Manifolds of Two There-Body Systems［J］.Journal of Astronautics，2007，28（3）：637-642.

［9］晁宁，李言俊.基于分段连续推力的晕轨道控制方法 ［J］.宇航学报，2011，32（9）：1925-1931.CHAO NING，LI YANJUN.A Halo Orbit Control Method Based on Segmental Continuous Thrust［J］.Journal of Astronautics，2011，32（9）：1925-1931.

［10］阙志宏，周凤岐，罗健，等.线性系统理论 ［M］.西安：西北工业大学出版社，1994.QUE ZHIHONG，ZHOU FENGQI，LUO JIAN，et al.Theory of linear system ［M］.Xi′an：Northwestern Poly-technical University Press，1994.