用最小二乘无网格有限差分方法求解二维浅水方程
陈善群,廖 斌,李海峰
(1.安徽工程大学建筑工程学院,安徽 芜湖 241000;2.中广核风力发电有限公司华南分公司,广东深圳 518031)
1 研究背景
在以海岸、河口、湖泊、大型水库等广阔水域地区为模型,进行流体数值模拟时,由于水平尺度远大于垂向尺度,水力参数(如流速、水深等)在垂直方向变化要明显小于水平方向的变化,其流态可用沿水深的平均流动量来表示。对于这些模型的数值模拟,可采用平面二维水动力数值模拟技术。二维水动力数值模拟技术中,使用的控制方程是将三维流动基本方程沿水深积分平均得到,又称为二维浅水方程。
对于二维浅水方程的求解,国内外学者已做了大量研究,目前主要的研究集中在2个方面:基于非结构网格的空间离散[1-2]和高性能的计算格式[3-4]。近年来兴起的无网格方法[5]具有无需划分网格、克服场函数局部化近似所引起的误差、仅需对边界条件进行描述、无需寻求光滑梯度场的后处理、适用于涉及大变形和需要动态调整的各类应用问题、适合进行自适应分析,以及求解精度较高等优点,已在固体力学数值计算领域得到成功的运用。在计算水力学,特别在求解二维浅水方程方面,运用无网格方法在国内还几乎是一片空白。
本文拟将最小二乘无网格有限差分方法(简称MLSFD方法)[6]运用于求解二维浅水方程,通过算例验证无网格方法在求解二维浅水方程中的可行性。
2 无网格有限差分方法的相关概念
2.1 支撑域[5]
以二维空间为例,如图1所示,将求解域Ω用n个节点离散,域中所有圆点即为相互独立的计算节点;在求解域计算节点中任找一个中心点(同心圆点),则此中心点的函数值可由它周围临近区域的计算节点通过一定的代数组合来逼近,我们称这种临近区域Ω为中心点的支撑域。
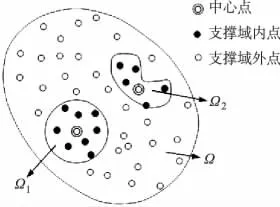
图1 节点支撑域Fig.1 Support domain of nodes
无网格方法的支撑域理论上可以是各种平面图形,但为了便于计算,在具体选择时一般取大小合适的圆形或矩形区域。图1中有2个支撑域,以圆形支撑域为例,同心圆点为支撑域中心点,实心黑点为支撑域内点,这两者一同组成“点云”参与中心点函数值的计算;而支撑域外点(空心圆点),我们认为其不参与中心点函数值的计算,对中心点的影响为0。
2.2 支撑域内点的选取原则
支撑域范围确定后,不是所有支撑域内的点都参与中心点的拟合计算。本文采用2种方法对支撑域内的点进行了选取[7]:
(1)拟定参与计算的点为n个,取支撑域内距离中心点最近的n个点即可。这种方法相当简单,耗机时较少;
(2)在前一种方法的基础上,对这n个点再进行一轮筛选。所选择点需尽量均匀分布在中心点周围(图2(a)),应避免在某个大扇形区域内无点(图2(b)),也要避免过小角度区域内有多个点(图2(c)),取扇形角度 在40°~120°之间。保证参与中心点计算的节点数为4~9个。在2个节点与中心点连接后夹角过小,需要舍弃1个时,保留离中心点近的节点(图2(c)),保留节点1,去掉节点2。这种方法相对前一种方法要耗机时,但计算点分布均匀。计算节点选取数量因中心点支撑域中离散点分布疏密的不同,为一不确定数。

图2 支撑域内点选取示意图Fig.2 Selection of interior nodes in support domain
2.3 最小二乘法的运用
无网格有限差分法计算导数近似值时会遇到这种情况:由于参与计算的支撑域内点相互之间非常靠近,造成的系数矩阵奇异和病态。这种问题并不容易解决,因为我们并不了解支撑域内的节点相互间的空间分布对系数矩阵造成的影响,除非这些节点在一条直线上。为了让数值计算进行下去,就得检验和确保系数矩阵在计算区域内的每个节点处都是良态的、可逆的,然而这种做法会大大增加计算机时。
为了避开繁琐的矩阵奇异、病态的检验过程,此处选用了最小二乘技术对矢量做最优化近似,具体实现就是选取足够多的支撑域内节点(大于要求解的导数数量),组成方程组进行计算,从而避开系数矩阵的奇异问题。
3 控制方程
本文选取控制方程为二维浅水方程非守恒形式,忽略柯氏力和风对模型的影响,最终形式为
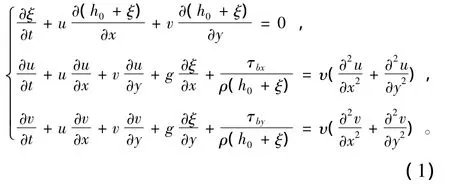
式中:u,v分别为流速在x,y方向的分量;h0为静水时的水深;ξ为自由水面在竖直方向的位移;τbx,τby分别为床面阻力在x,y方向的分量。
4 控制方程的离散
MLSFD方法的离散形式[8]为:
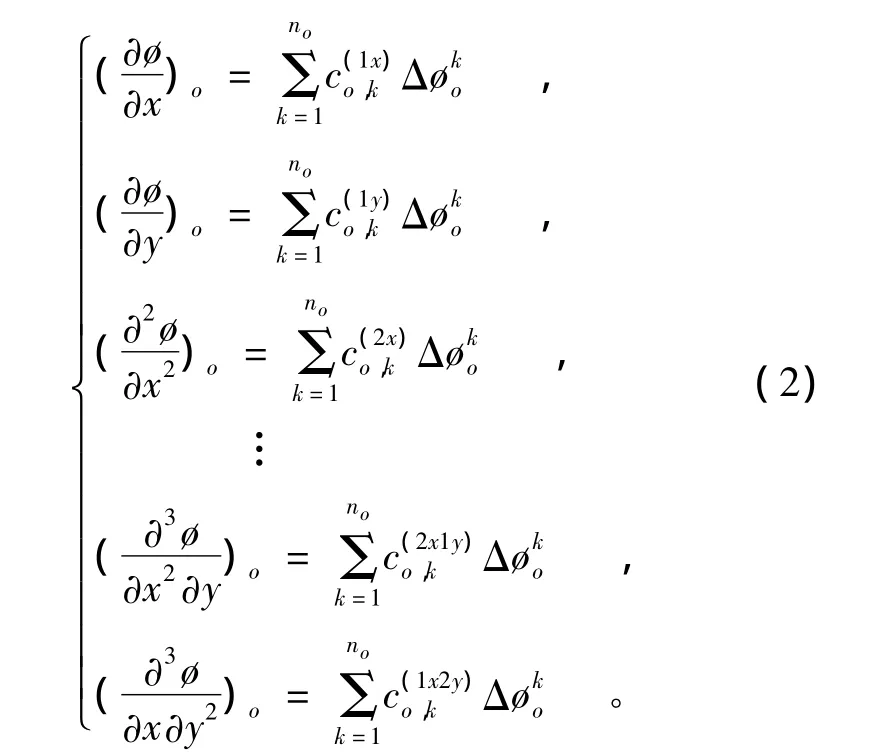
将式(2)代入式(1)的空间导数中,时间上仍采用向前差分格式,得到二维浅水方程的MLSFD离散式:

5 圆形溃坝模型
数值计算中,常用圆形溃坝模型来检验算法在处理对称间断流方面的能力。本文将使用MLSFD(Meshfree Least-Squares-based Finite Difference Method)方法对该模型进行计算。
5.1 计算模型具体设置及初始条件
模型具体设置及初始条件:计算区域为一长和宽都为50 m的正方形区域,区域中心设置一半径11 m,水深10 m的圆形水坝,其他区域水位为1 m,在某一时刻圆形水坝突然溃决。图3为圆形溃坝模型初始时刻水位示意图。为提高计算精度,时间步长取0.001 s。

图3 圆形溃坝初始水位Fig.3 Initial water level for the circular dam-break model
5.2 计算模型网格划分及边界条件
如图4所示,计算区域中心采用无网格随机布点,计算节点总数为11 823个。计算模型四周边界条件为:x 方向∂u/∂x=0,∂v/∂x=0,∂ξ/∂x=0;y 方向∂u/∂y=0,∂v/∂y=0,∂ξ/∂y=0。
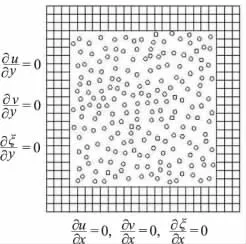
图4 圆形溃坝模型网格划分Fig.4 Mesh generation for the circular dam-break model
5.3 计算模型边界处理
为了更好地处理边界条件,我们在无网格的四周,向内分别布置了3层直角网格。需要注意的是,这种特殊的网格布置,仅仅是用来处理边界条件的。除最外层边界上的点,其他所有点包括直角网格上的节点,仍采用MLSFD格式计算。如图5所示,在边界上的w点的函数值,根据边界条件,可以由内层的w+1,w+2点的函数值来求得。令ø表示节点处的函数值,则边界条件为∂ø/∂xi=0,通过一维泰勒级数在这3点上的展开式,可以求得w点的有限差分格式:
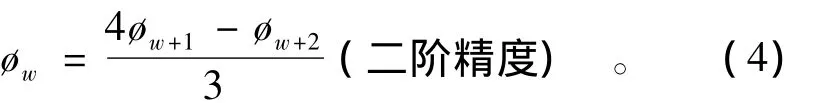
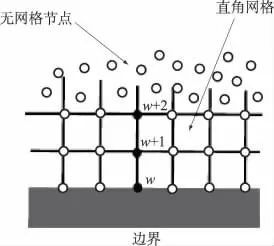
图5 圆形溃坝模型边界处理Fig.5 Boundary treatment for the circular dam-break model
5.4 计算结果分析
计算时选取支撑域内离中心点距离最近的17个点,将初始值和边界条件处理格式代入式(3),在每一时间步迭代求解,得出0.69 s时圆形溃坝模型计算模拟结果(图6、图7、图8)。图6中所示的圆形溃坝0.69 s时的水位呈尖锥形,顶部水位最高。由于是突然溃决,上面溃决的水体对下面的水体有向下的冲击作用,这样就在水位尖锥底部周围形成了一个环形的浅水坑。图7中所示的圆形溃坝0.69 s时的水位等值线呈圆环状,分布比较均匀,其中圆环中心处的水位接近10.0 m,边缘处水位接近1.0 m。图6、图7所示的数值模拟结果与 Mingham[9]采用的极坐标网格计算的结果相当吻合。图8中所示的速度矢量均匀发散,中心处速度最小,边缘处速度最大,说明圆形水体是从边缘往中心处溃决,这与实际情况相符。
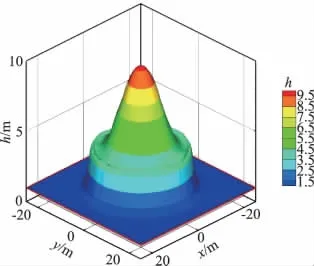
图6 圆形溃坝0.69 s时的水位Fig.6 Water level for the circular dam break at t=0.69 s

图7 圆形溃坝0.69 s时的水位等值线Fig.7 Contour plot of water level for the dam break at t=0.69 s
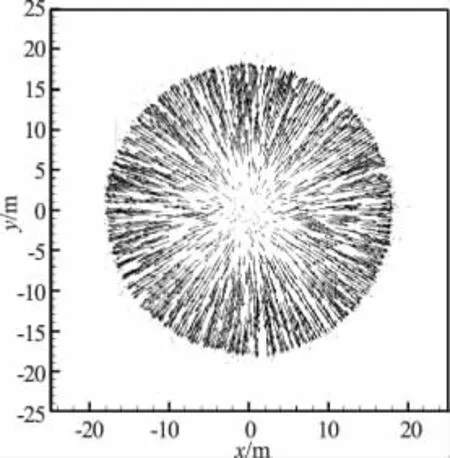
图8 圆形溃坝0.69 s时的速度矢量Fig.8 Velocity vectors for the dam break at t=0.69 s
6 结论
本文将最小二乘无网格有限差分(MLSFD)方法运用于求解二维浅水方程,利用最小二乘无网格有限差分离散式对二维方程进行了离散求解。在计算圆形溃坝这一典型数值算例时,对计算区域进行离散布点,利用泰勒离散式处理边界条件,得出了0.69 s时圆形溃坝的水位图、水位等值线图以及速度矢量图。并对数值模拟结果进行分析比较,验证了该方法在计算二维浅水流动的数值模拟方面有着较高的精确度,进而说明无网格方法运用于求解浅水方程是可行的。
[1]杨 彬,汪德爟.非结构网格上浅水方程的LU-SGS隐式算法[J].河海大学学报(自然科学版),2008,36(4):483 -487.(YANG Bin,WANG De-guan.LU-SGS Scheme for Shallow Water Equation Computation on Unstructured Grids[J].Journal of Hohai University(Natural Sciences),2008,36(4):483 -487.(in Chinese))
[2]卢康明,李光炽.非结构网格浅水方程隐式解法[J].水动力学研究与进展(A辑),2010,25(2):247-253.(LU Kang-ming,LI Guang-chi.An Implicit Method for Shallow Water Equations on Unstructured Grids[J].Chinese Journal of Hydrodynamics,2010,25(2):247 - 253.(in Chinese))
[3]潘存鸿.三角形网格下求解二维浅水方程的和谐Godunov格式[J].水科学进展,2007,18(2):204 -209.(PAN Cun-hong.Well-balanced Godunov-type Scheme for 2D Shallow Water Flow with Triangle Mesh[J].Advances in Water Science,2007,18(2):204 - 209.(in Chinese))
[4]潘存鸿,徐 昆.三角形网格下求解二维浅水方程的KFVS格式[J].水利学报,2006,37(7):858-864.(PAN Cun-hong,XU Kun.Kinetic Flux Vector Splitting Scheme for Solving 2D Shallow Water Equations with Triangular Mesh[J].Journal of Hydraulic Engineering,2006,37(7):858 -864.(in Chinese))
[5]张 雄,刘 岩.无网格法[M].北京:清华大学出版社,2004.(ZHANG Xiong,LIU Yan.Meshless Methods[M].Beijing:Tsinghua University Press,2004.(in Chinese))
[6]DING H,SHU C.Simulation of Incompressible Viscous Flows Past a Circular Cylinder by Hybrid FD Scheme and Meshless Least Square-based Finite Difference Method[J].Computer Methods in Applied Mechanics and Engineering,2004,193:727 -744.
[7]江兴贤,陈红全,Euler方程无网格算法及布点技术[J].南京航空航天大学学报,2004,36(2):174 -178.(JIANG Xing-xian,CHEN Hong-quan.Gridless Method for Euler Equations and Distributing Point Technique[J].Journal of Nanjing University of Aeronautics &Astronautics,2004,36(2):174 -178.(in Chinese))
[8]DING H,SHU C.Development of Least-Square-Based Two-Dimensional Finite-Difference Schemes and Their Application to Simulate Natural Convection in a Cavity[J].Computers& Fluids,2004,(33):137 -154.
[9]MINGHAM C G,CAUSON D M.High-Resolution Finite-Volume Method for Shallow Water Flows[J].Journal of Hydraulic Engineering,1998,124(6):605-614.

