一类带梯度项椭圆方程解的存在性
刘广刚, 韦玉程,2
(1. 吉林大学 数学学院, 长春 130012; 2. 河池学院 数学系, 广西 河池 546300)
0 引 言
考虑椭圆方程边值问题:

(1)
解的存在性, 其中Ω⊂RN(N≥3)是一个光滑有界区域. 由于右端项f含有梯度项, 问题(1)不具有变分结构, 因此不能直接用变分法研究其解的存在性. 这种情形下最常用的工具是拓扑度理论, 为得到问题上下解和解的先验估计, 通常需要对非线性项做适当假设, 这方面的研究目前已有许多结果[1-6]. 文献[7]通过先固定梯度项再利用山路引理和迭代技巧, 在f满足超线性增长条件时证明了问题(1)正解和负解的存在性. 该方法在拟线性微分方程[8-9]、 Hamilton系统[10]和脉冲微分方程[11]中应用广泛. 文献[7-11]均要求右端非线性项满足超线性增长条件. 本文考虑f满足渐近线性增长条件时, 问题(1)正解和负解的存在性.
设0<λ1<λ2≤λ3≤…≤λk≤…是-Δ对应于Dirichlet条件的特征值列. 假设:
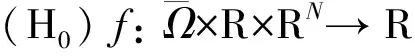
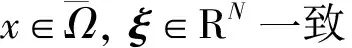

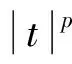
(H4)f(x,t,ξ)关于t,ξ满足全局Lipschitz条件, 即存在常数L>0, 使得
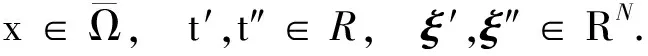
由条件(H1), 0是问题(1)的一个解, 称为平凡解. 本文考虑问题(1)非平凡解的存在性, 主要结果如下:
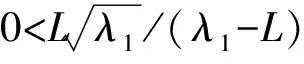
1 引 理
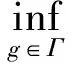

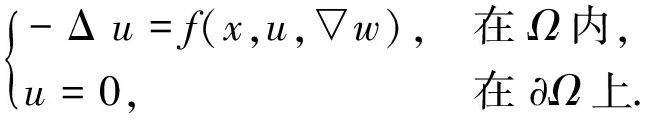
(2)
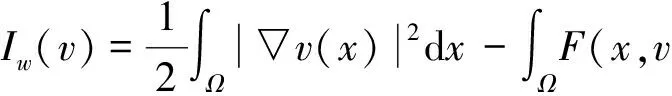

(x),▽w(x))dx.

证明: 由文献[12]中命题B35可知, 只需证明{un}有界即可.
记u+(x)=max{u(x),0}. 由条件(H2), 存在常数M1>0, 使得



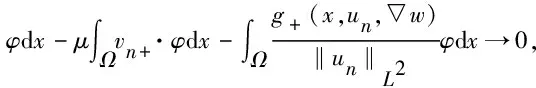
(3)
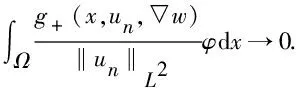
-Δv=μv+.
(4)
由最大值原理知v>0或v=0. 如果v>0, 则v是-Δ的一个正的特征函数, 因此μ=λ1, 这与条件(H2)矛盾. 故v=0, 但这又与‖v‖L2=1矛盾. 从而序列{un}有界. 证毕.
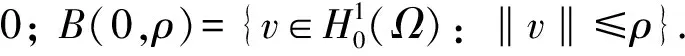
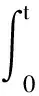
由条件(H1)知,λ<λ1, 故取充分小可使1-λ/λ1-/λ1>0. 又因为p+1>2, 所以当ρ充分小时, (1-λ/λ1-/λ1)ρ2/2-Ckρp+1>0. 取这样的ρ, 令β=(1-λ/λ1-/λ1)ρ2/2-Ckρp+1, 则有Iw+(v)>β, ∀v∈∂B(0,ρ). 证毕.
引理3假设(H0),(H1),(H2),(H3)成立, 则存在v0∉B(0,ρ), 使得Iw+(v0)<0.
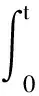
令φ1为-Δ的对应于λ1的特征函数, 则φ1(x)>0. 因此,
由(H2)知μ>λ1, 故可取充分小, 使得λ1-μ+<0. 由式(5)知, 存在T, 使得当t≥T时, 有Iw+(Tφ1)<0. 取v0(x)=Tφ1(x), 则由引理2知,v0(x)∉B(0,ρ), 且Iw+(v0)<0. 证毕.
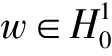

▽w)uw-dx=0.
因此,uw(x)≥0. 又由最大值原理知, ∀x∈Ω,uw(x)>0, 且∀x∈∂Ω, ∂uw/∂ν<0, 其中ν是∂Ω上的指向外侧的单位法向量. 故uw也是Iw的临界点, 从而问题(2)至少有一个非平凡的正解uw. 证毕.
引理5存在不依赖于w的常数c1>0, 使得问题(2)的非平凡解uw都满足‖uw‖≥c1.
证明: 由uw是问题(2)的弱解得
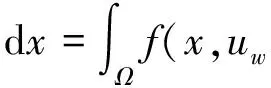
(6)
特别地, 取φ(x)=uw(x)代入式(6)有
(x),▽w(x))uw(x)dx.
由条件(H1)和(H3), 任取>0, 存在常数k>0, 满足g0(x,t,ξ)≤t+k. 则由Sobolev不等式, 有
从而由式(7)得
因为λ<λ1, 取>0充分小, 使得1-λ/λ1-/λ1>0, 并注意到p+1>2, 所以存在常数c1>0, 使得对任意的问题(2)的非平凡解uw都有‖uw‖≥c1. 证毕.
2 定理1的证明
(8)
由Schauder正则性理论[13]可知, ∀x∈Ω,un∈C2,α(Ω,R), 且un>0. 由于un+1和un满足:
-Δun+1=f(x,un+1,▽un), -Δun=f(x,un,▽un-1),
因此
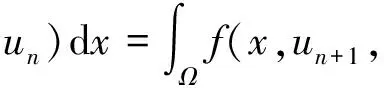
(9)
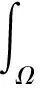
(10)

从而
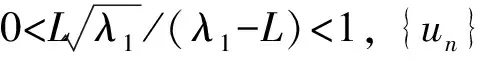
衷心感谢吉林大学数学学院史少云教授的悉心指导.
[1] Amann H, Crandall M G. On Some Existence Theorems for Semilinear Elliptic Equations [J]. Indiana Univ Math J, 1978, 27: 779-790.
[2] Pohozaev S. On Equations of the Type Δu=f(x,u,Du) [J]. Mat Sb, 1980, 113: 324-338.
[3] Xavier J B M. Some Existence Theorems for Equations of the Form -Δu=f(x,u,Du) [J]. Nonlinear Analysis TMA, 1990, 15(1): 59-67.
[4] WANG Xu-jia, DENG Yin-bing. Existence of Multiple Solutions to Nonlinear Elliptic Equations in Nondivergence Form [J]. J Math Anal and Appl, 1995, 189(3): 617-630.
[5] YAN Zi-qian. A Note on the Solvability inW2,p(Ω) for the Equation -Δu=f(x,u,Du) [J]. Nonlinear Analysis TMA, 1995, 24(9): 1413-1416.
[6] YAN Zi-qian. The Solvability of the Equation -Δu=f(x,u,Du) inW2,p(Ω) [J]. Acta Scientiarum Naturalium Universitatis Jilinensis, 1992(2): 30-32. (严子谦. 方程-Δu=f(x,u,Du)在W2,p(Ω)中的可解性 [J]. 吉林大学自然科学学报, 1992(2): 30-32.)
[7] Figuereido D G, de, Girardi M, Matzeu M. Semilinear Ellptic Equations with Dependence on the Gradient via Mountain-Pass Techniques [J]. Differential and Integral Equations, 2004, 17: 119-126.
[8] Girardi M, Matzeu M. A Compactness Result for Quasilinear Elliptic Eqations by Mountain Pass Techniques [J]. Rend Math Appl, 2009, 29(1): 83-95.
[9] Servadei R. A Semilinear Elliptic PDE Not in Divergence Form via Variational Methods [J]. J Math Anal Appl, 2011, 383(1): 190-199.
[10] Girardi M, Matzeu M. Existence of Periodic Solutions for Some Second Order Quasilinear Hamiltonian Systems [J]. Rend Lincei Mat Appl, 2007, 18(1): 1-9.
[11] TENG Kai-min, ZHANG Chao. Existence of Solution to Boundary Value Problem for Impulsive Differential Equations [J]. Nonlinear Anal RWA, 2010, 11(5): 4431-4441.
[12] Rabinowitz P H. Minimax Methods in Critical Point Theory with Applications to Differential Equations [M]. Providence: Amer Math Soc, 1986.
[13] Gilbarg D, Trudinger N S. Elliptic Partial Differential Equations of Second Order [M]. 2nd ed. Berlin: Springer, 1983.

