Banach 空间中含(A，η，m)-增生算子的一类新广义非线性集值变分包含组*

祝 聪， 倪仁兴

(1．浙江师范大学 数理与信息工程学院，浙江 金华 321004;2．绍兴文理学院 数学系，浙江 绍兴312000)

0 引言

1970年，Brezis［1］在讨论变分不等式问题时最先提出了“预解算子”的概念;随后，Hassouni和Moudafi［2］将它作了改进和完善．Noor［3］在预解算子的基础上又提出了预解方程并建立了它和混合变分不等式之间的等价关系．近几年来，预解算子技术在发展不同类型的变分不等式(或变分包含)的迭代算法和研究解的存在性受到了国内外许多学者的兴趣［4-15］．例如：2006年，Lan等［8］引进了(A，η)-增生映射的概念及含(A，η)-增生映射的预解算子的定义，同时使用该类预解算子解决了一类变分包含问题;2007年，Xia等［9］引入了广义H-单调算子，并在Banach空间中研究了带有广义H-单调算子的变分包含问题;特别地，2009年，Yang等［14］在Banach空间中研究了如下一类广义非线性集值变分包含系统：对 i=1，2，设 s，p，g，Ai：X→X 为单值映射，Ni，ηi：X × X→X 为单值映射，T，Q：X→2X为集值映射，Mi：X→X 为(Ai，ηi)-增生映射．寻找 x，y∈X，使得 g(x)∈dom(M1)且

他们证明了所构造的算法强收敛于该类广义非线性集值变分包含的解．

受上述结果的启发，本文在一般Banach空间框架中，对广义预解算子，通过构造新的更为广泛的变分包含系统，且在假定它的解存在的情况下，在适当的条件下给出了迭代序列强收敛的新结果．

1 预备知识

全文均设X是实Banach空间，X*为X的对偶空间，〈u，v〉是u∈X*与v∈X间的对偶对．R+为正实数集．广义对偶映射 Jq：X→2X*定义如下：Jq(x)={f*∈X*：〈x，f*〉=‖x‖q，‖f*‖ =‖x‖*}，∀x∈X．其中q＞1为常数．特别地，J2为正规对偶映射．显然，Jq(x)=‖x‖q－2J2(x)对所有x≠0成立．如果X=H是Hilbert空间，那么，J2就是恒等映射I．

X 的光滑模 ρX：［0，∞)→［0，∞)定义为

引理1［16］设X是一致光滑实的Banach空间，则X是q-一致光滑的充要条件是：存在常数Cq＞0，使得

式(1)中：λ1，λ2∈R+是固定参量;β∈［0，1)．以下是问题(1)的特殊情况：

1)若 p2=0，Ni(·，·，·)=Ni(·，·)，Mi(·，·)=Mi(·)，gi(·，·)=gi(·)(i=1，2)，g2=I，β =0，则问题(1)等价于寻找 x，y∈X，满足

问题(2)即为文献［14］中的一类新广义非线性集值变分包含系统．

2)若 X=H 是 Hilbert空间，Mi(·，·)=Mi(·)是(Hi，ηi)-单调算子，g1=I，则问题(2)等价于寻找 x1，x2∈H，满足

定义1［8］设S：X→X，N：X×X×R+→X都是单值映射．称单值映射N为：

1)对第1个变元关于映射S是(a，b)-松弛余强制，如果存在常数a，b＞0，使得

定义2［8］若 η：X ×X→X，A：X→X 为单值映射，则称集值映射M：X→2X为：

1)r-强 η-增生，如果存在常数 r＞0，对任意 x，y∈X，u∈M(x)，v∈M(y)，有

2)m-松弛 η-增生，如果存在常数 m ＞0，对任意 x，y∈X，u∈M(x)，v∈M(y)，有

3)(A，η，m)-增生，如果 M 是 m-松弛 η-增生且(A+ρM)(X)=X，∀ρ＞0．

其中，λ＞0是常数．

2 主要结果

在假定问题(1)有解的前提下，对(A，η，m)-增生映射，运用广义预解算子技术，探讨问题(1)解的迭代逼近问题．

引理4 对任意给定的x，y∈X，(x，y)是问题(1)的解等价于

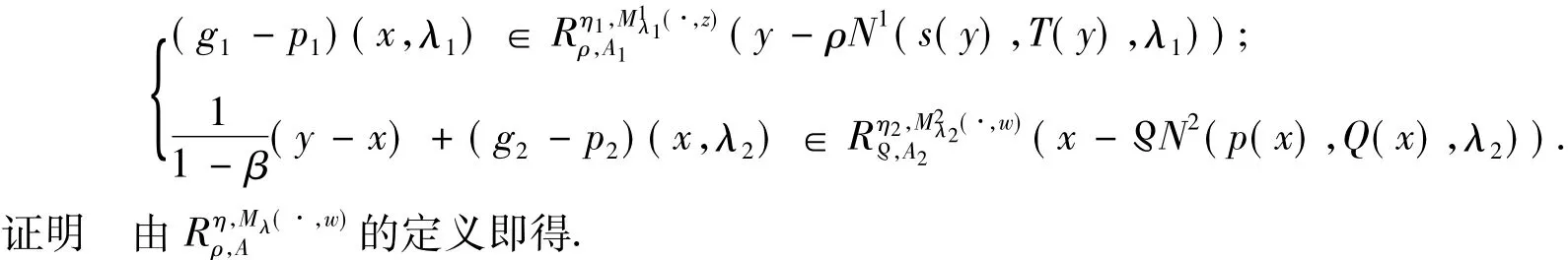
受上述方程的启发，构造以下Ishikawa型迭代算法：

算法1 对任给x0∈X，记

算法2 对任给x0∈X，记

算法2即为文献［14］所讨论的迭代算法，其收敛性问题Yang等［14］已作过仔细的研究和探讨．

若X=H是Hilbert空间，Mi(·，·)=Mi(·)，g1=I，则算法2等价于下面的算法3，可解决问题(3)：

算法3 对任给x0∈X，记

定理1 设 X 是 q-一致光滑实 Banach空间．对 i=1，2，gi－pi：X ×R+→X 为(ai，bi)-松弛余强制且γi-Lipschitz连续，s，p：X→X 为 μ，κ-Lipschitz连续，T，Q，E，G：X→CB(X)分别为 θ，δ，ξ，ζ-H-Lipschitz连续，N1：X×X×R+→X关于第1元和第2元分别为 μ1，β-Lipschitz连续且相对于第1元关于s是(α1，β1)-松弛余强制，N2：X×X×R+→X关于第1元和第2元分别为μ2，β'-Lipschitz连续且相对于第1元关于 p 是(α2，β2)-松弛余强制，ηi：X × X→X 是 τi-Lipschitz 连续，Ai：X→X 为 ri-强 ηi-增生，Mi：X × X ×R+→2X为(Ai，ηi，mi)-增生映射，且∃υ1，υ2＞ 0，使得

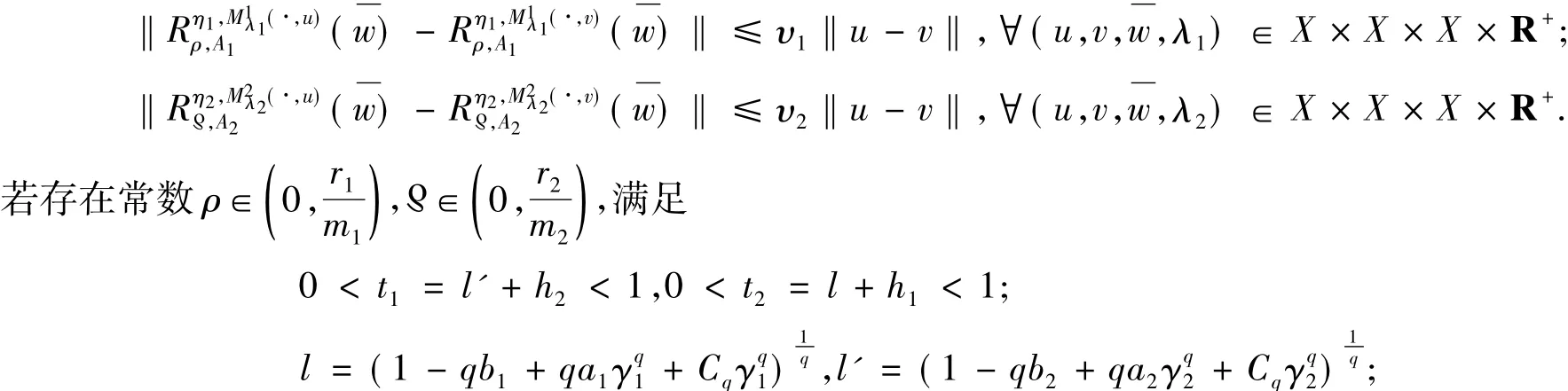
假设问题(1)有解，那么由算法1定义的迭代序列{xn}，{yn}强收敛于问题(1)的解．证明 设(x*，y*)是问题(1)的解，则由引理4有

由于 T(yn)，T(y*)，E(yn)，E(y*)，Q(yn)，Q(x*)，G(xn)，G(x*)∈CB(X)，∀n≥0，则对任给的 ε ＞0，由 Nadler引理知，∃vn∈T(yn)，un∈Q(xn)，zn∈E(yn)，wn∈G(xn)，有

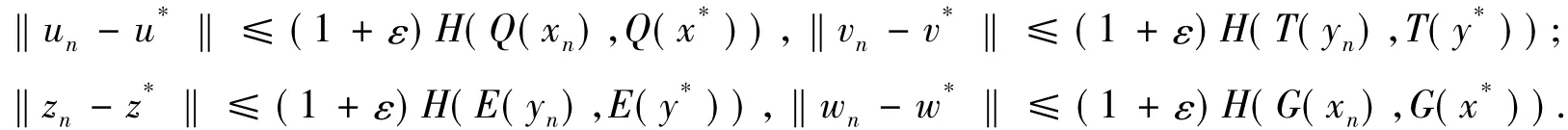
则由算法1和引理2有

而由引理1知，g1－p1为(a1，b1)-松弛余强制和 γ1-Lipschitz连续，得

另外，

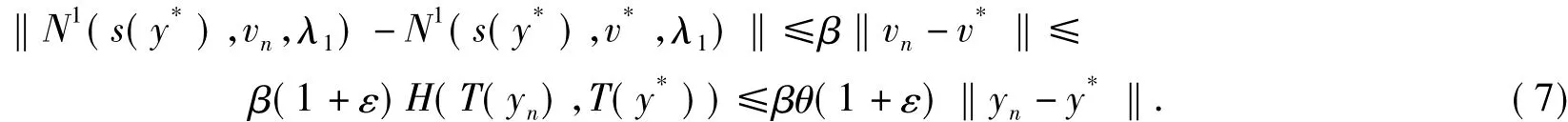
再次利用了引理1，N1的Lipschitz连续和关于第1元是(α1，β1)-松弛余强制的，得

把式(6)～式(8)代入式(5)，得

式(9)中：

由于{βn}为一实数序列，且 βn∈［0，1)，故类似可得

故

其中：

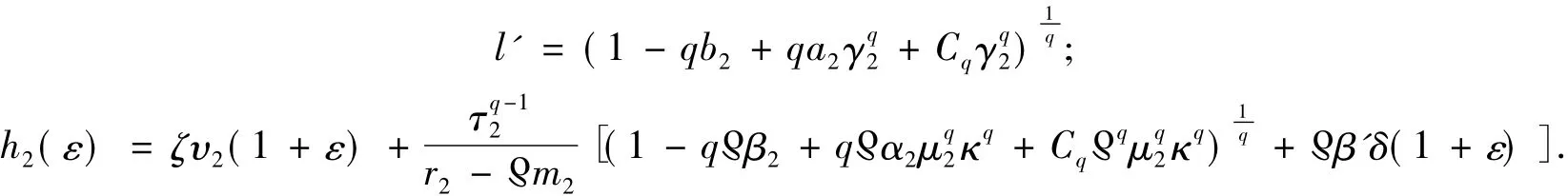
把式(10)代入式(9)并整理得

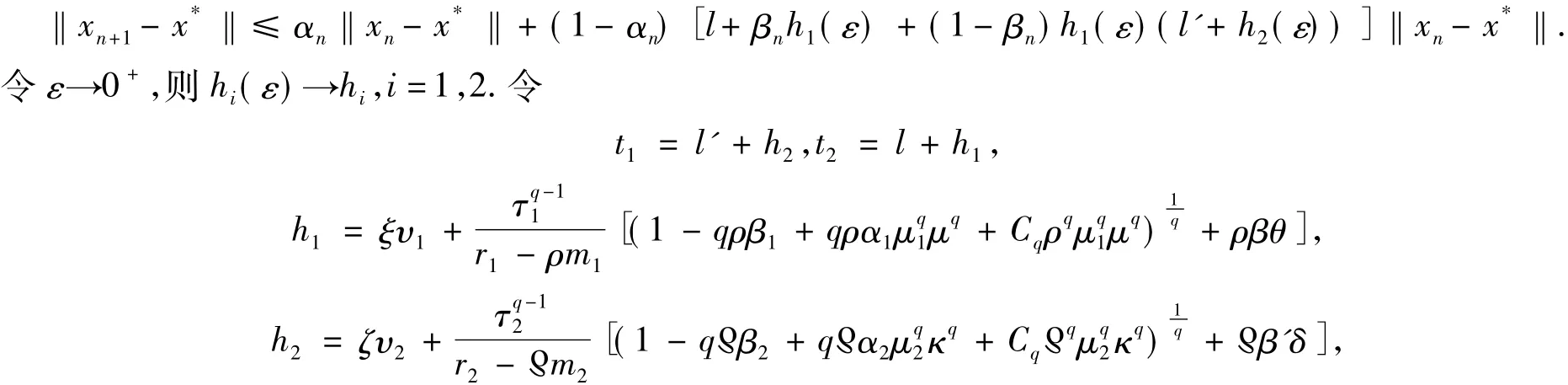
则

根据条件 βn∈［0，1)，0 ＜t1=l'+h2＜1，得

定理1 中若 pi=0，Ni(·，·，·)=Ni(·，·)，Mi(·，·)=Mi(·)，gi(·，·)=gi(·)(i=1，2)，g2=I，β =0，即得文献［14］中的定理3．1;进一步，若 g1=I，则得文献［14］中的定理3．2．

推论1 设 X=H 是实 Hilbert空间．对 i=1，2，s，p：H→H 为 μ，κ-Lipschitz连续，T，Q：H→CB(H)分别为θ，δ-H-Lipschitz连续，N1：H×H→H关于第1元和第2元分别为 μ1，β-Lipschitz连续且相对于第1元关于 s是(α1，β1)-松弛余强制，N2：H ×H→H 关于第1元和第2 元分别为 μ2，β'-Lipschitz连续且相对于第1 元关于 p 是(α2，β2)-松弛余强制，ηi：H × H→H 是 τi-Lipschitz连续，Ai：H→H 为 ri-强 ηi-单调，Mi：H→2H为(Hi，ηi)-单调算子，若存在常数 ρ＞0，■ ＞ 0，满足

假设问题(3)有解，那么由算法3定义的迭代序列{xn}，{yn}强收敛于问题(3)的解．

定义4［19］若 η：H×H→H，T：H→H为2个单值映射，φ：H→R∪{+∞}为具 η-次微分的真函数，若对任意 x∈H，ρ＞0，存在唯一点 u∈H 满足〈Tu，η(y，u)〉≥ρφ(u) －ρφ(y)，∀y∈H，那么映射x→u 定

引理5［21］若 T：H→H 为 γ-强 η-单调，η：H × H→H 为 σ-Lipschitz连续，满足∀x，y∈H，η(x，y)=－η(y，x)，并且对任给的 x∈H，函数 h(y，u)=〈x－ Tu，η(y，u)〉关于 y是 0-对角拟凹的，φ：H→R∪{+ ∞}为具 η-次微分的真函数，那么∂ηφ 是(T，η)-单调的．

算法4 对任给x0∈X，记

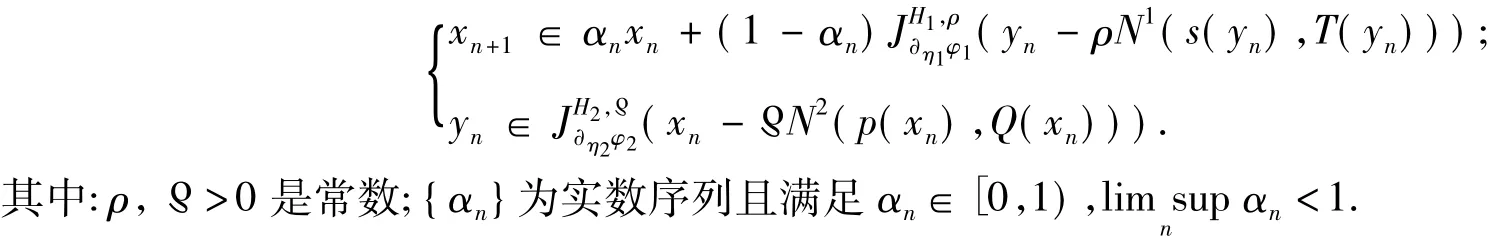
推论2 设 X=H 是实 Hilbert空间．对 i=1，2，ηi：H ×H→H 是 τi-Lipschitz连续，Hi：H→H 为 ri-强ηi-单调，满足∀xi，yi∈H，ηi(xi，yi)= － η(yi，xi)，并且对任给的 xi∈H，函数 hi(yi，ui)=〈xi－ Hiui，ηi(yi，ui)〉关于 yi是0-对角拟凹的，φi：H→R∪{+∞}为 ηi-次微分函数，s，p：H→H 为 μ，κ-Lipschitz连续，T，Q：H→CB(H)分别为 θ，δ-H-Lipschitz连续，N1：H ×H→H 关于第 1 元和第 2 元分别为 μ1，β-Lipschitz连续且相对于第1元关于s是(α1，β1)-松弛余强制，N2：H×H→H关于第1元和第2元分别为μ2，β'-Lipschitz连续且相对于第 1 元关于 p 是(α2，β2)-松弛余强制，ηi：H × H→H 是 τi-Lipschitz连续，Ai：H→H为 ri-强 ηi-单调，Mi：H→2H为(Hi，ηi)-单调算子，若存在常数，满足

假设问题(4)有解，那么由算法4定义的迭代序列{xn}，{yn}强收敛于问题(4)的解．

［1］Brezis H．Operateur maximaux monotones et semigroups de contractions dans les espaces de Hilbert［M］．Amaterdam：Norh-Holland，1973．

［2］Hassouni A，Moudafi A．A perturbed algorithm for variational inclusions［J］．J Math Anal Appl，1994，185(3)：706-712．

［3］Noor M A．Some recent advances in variational inequalities，Part I：Basic concepts［J］．New Zealand J Math，1997，26：53-80．

［4］黄南京，方亚平．Banach 空间中的广义 m-增生映像［J］．四川大学学报：自然科学版，2001，38(4)：591-592．

［5］Fang Y P，Huang N J．H-monotone operators and resolvent operator technique for variational inclusions［J］．Appl Math Comput，2003，145(2/3)：795-803．

［6］Fang Y P，Huang N J．H-accretive monotone operators and resolvent operator technique for solving variational inclusions in Banach spaces［J］．Appl Math Lett，2004，17(6)：647-653．

［7］Fang Y P，Huang N J，Thompson H B．A new system of varitional inclusions with monotone operators in Hilbert spaces［J］．Comput Math Appl，2005，49(2/3)：365-374．

［8］Lan H Y，Cho Y J，Verma R U．On nonlinear relaxed cocoercive variational inclusions involving accretive mappings in Banach spaces［J］．Comput Math Appl，2006，51(9/10)：1529-1538．

［9］Xia Fuquan，Huang Nanjing．Variational inclutions with a generalized H-monotone operator in Banach spaces［J］．Comput Math Appl，2007，54(1)：24-30．

［10］Verma R U．Projection methods，algorithms，and a new system of nonlinear variational inequalities［J］．Comput Math Appl，2001，41(7/8)：1025-1031．

［11］Verma R U．Generalized system for relaxed coercive variational inequalities and projection methods［J］．J Optim Theory Appl，2004，121(1)：203-210．

［12］Kim J K，Kim D S．A new system of generalized nonlinear mixed variational inequalities in Hilbert spaces［J］．Journal of Convex Analysis，2004，11(1)：235-243．

［13］Lan H Y，Huang N J，Cho Y J．New iterative approximation for a system of generalized nonlinear variational inclusions with set-valued mappings in Banach spaces［J］．J Math Inequal Appl，2006，9(1)：175-187．

［14］Yang Y Q，Jin M M，Ling F．A new system of generalized nonlinear set-valued variational inclusions in Banach spaces［J］．Math Inequal Appl，2009，16：81-91．

［15］Lan H Y．Sensitivity analysis for generalized nonlinear parametric(A，η，m)-maximal monotone operator inclusion systems with relaxed cocoercive type operators［J］．Nonlinear Analysis：TMA，2011，74(2)：386-395．

［16］Xu H K．Inequalities in Banach spaces with applications［J］．Nonlinear Anal TMA，1991，16(12)：1127-1138．

［17］Ding X P，Feng H R．The p-step iterative algorithm for a system of generalized mixed quasi-variational inclusions with(A，η)-accretive operators in q-uniformly smooth Banach spaces［J］．J Comput Appl Math，2008，220(1/2)：163-174．

［18］Fang Y P，Huang N J．Iterative algorithm for a system of variational inclusions involving H-accretive operators in Banach spaces［J］．Acta Math Hungar，2005，108(3)：183-195．

［19］Ding X P．Generalized quasi-variational-like inclusions with nonconvex functionals［J］．Appl Math Comput，2001，122(3)：267-282．

［20］赵亚莉，钱伟懿，白乙拉．广义似变分不等式解的存在性和算法［M］．大连：大连理工大学出版社，2008．

［21］Ahmad R，Siddiqi A H，Khan Z．Proximal point algorithm for generalized multivalued nonlinear quasi-variational-like inclusions in Banach spaces［J］．Appl Math Comput，2005，163(1)：295-308．