关于数论函数方程 φ(n)=s(n9)
陈 燕, 魏其矫
(成都信息工程学院数学学院,四川成都610225)
“著名的美籍罗马尼亚数学家Florentin Smarandache同时拥有许多其他身份,如诗人、作家、多种语言的翻译家、哲学家、物理学家等。他不是一般的作家,在1999年他获得诺贝尔文学奖提名!Smarandache函数是他在那本很有名或者很有趣的书《只有问题,没有解答!》中提出来的,”各种数论函数的性质一直是一个令人感兴趣的问题.对于正整数 n,与 φ(n)和 s(n)有关的函数方程 φ(n)=s(nt),前人做过一些研究[1-13],文中讨论 t=9时的情形.
1 定义及引理
定义1[14]Euler函数:表示不大于n且与n互素的正整数的个数,记作:φ(n).
定义2[15]Smarandache函数:表示使得的最小的正整数 m,记作s(n),即 s(n)=min{m∈z+
引理1[14]Euler函数是积性函数,即对互素的正整数 a和b,φ(ab)=φ(a)φ(b).
引理2[14]如果是n的标准分解式,则
引理3 当 n>2时,φ(n)必为偶数.
证明(i)如果n有奇素因数p,则 p-1是偶数.
(ii)如果没有奇素因数,则因 n>2,故有n=2r,其中 r是大于1的正整数.此时,根据引理2可知:φ(n)=2r-1也是偶数.
引理4[15]如果是n的标准分解式,则

引理5[15]对于素数p和正整数k,有s(pk)≤kp成立.
如果k<p,那么s(pk)=kp,其中k为任意给定的正整数.
2 定理及其证明
定理 当 t=9时,方程
φ(n)=s(nt)
仅有解n=1.
证明 当 t=9时,方程 φ(n)=s(nt)可写成 φ(n)=s(n9).
接下来,对这一方程进行求解:
(1)当 n=1时,显然是方程的解.
(2)当 n>1时,根据引理 4可设:
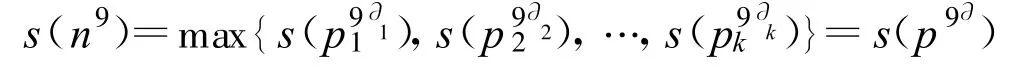
其中 p是n的素因数,∂是p在n中的次数.
此时,根据引理1可得:

那么,方程 φ(n)=s(n9),可变为
p∂-1(p-1)φ(n1)=s(p9∂)
若存在p使上述等式成立,则验证s(n9)=s(p9∂)是否成立.若成立,则 p是方程φ(n)=s(n9)的解.若不成立,则 p不是方程φ(n)=s(n9)的解.
那么 ,有
(i)当∂=1 时,方程可变为(p-1)φ(n1)=s(p9),则
若 p=2,那么s(29)=12=φ(n1),则 n1=13,由引理 5易知,该方程无解.
若 p=3,那么 s(39)=21=2φ(n1),显然 21=2φ(n1)无整数解.
若 p=5,那么 s(59)=40=4φ(n1),则 n1=11,该方程无解.
若 p=7,那么 s(79)=56=6φ(n1),该方程无解.
若 p ≥11,那么 s(p9)=9p,φ(n)=(p-1)φ(n1),注意到 pł(p-1)φ(n1),因此 ,该方程无解.
(ii)当∂=2时,方程可变为 p(p-1)φ(n1)=s(p18),则
若 p=2,那么s(218)=20=2φ(n1),则 n1=11,该方程无解.
若 p=3,那么 s(318)=39=3*2 φ(n1),无解 .
若 p=5,那么 s(518)=75=5*4φ(n1),该方程无解.
若 p=7,那么s(718)=112=6*7φ(n1),该方程无解.
若 p=11,那么 s(1118)=187=11*10φ(n1),无解.
若 p=13,那么 s(1318)=221=13*12φ(n1),无解.
若 p=17,那么 s(1718)=289=17*16φ(n1),无解.
若 p≥19,那么 n=1,64,72,80φ(n)=p(p-1)φ(n1),注意到(p-1)φ(n1)>18,因此,该方程无解.
(iii)当∂=3时,方程可变为 p2(p-1)φ(n1)=s(p27),则
若 p=2,那么 s(227)=32=22φ(n1),则 n1=15或 16,而 2| 16,所以16不是方程的解.当 n1=15,于是 n=15*23=120,然而s(1209)=s(59)=40≠s(227)=32.因此,该方程无解.
若 p=3,那么 s(327)=57=32*2φ(n1),无解.
若 p=5,那么 s(527)=115=52*4φ(n1),该方程无解 .
若 p=7,那么 s(727)=168=72*6φ(n1),该方程无解 .
若 p=11,那么 s(1127)=275=112*10 φ(n1),无解.
若 p=13,那么 s(1327)=338=132*12 φ(n1),无解.
若 p=17,那么 s(1727)=442=172*16 φ(n1),无解.
若 p=19,那么 s(1927)=494=192*18 φ(n1),无解.
若 p=23,那么 s(2327)=598=232*22 φ(n1),无解.
若 p≥29,那么 s(p27)=27p=φ(n)=p2(p-1)φ(n1),注意到 p2>27p,因此,该方程无解.
(iv)当∂=4 时,方程可变为 p3(p-1)φ(n1)=s(p36),则
若 p=2,那么 s(236)=40=23φ(n1),该方程无解 .
若 p=3,那么 s(336)=78=33*2φ(n1),无解.
若 p ≥5,由引理 5 可知 :s(p9∂)≤9p∂,注意到 φ(n)=p∂-1(p-1)φ(n1)和 p∂-1(p-1)>9p∂,因此 ,该方程无解.
(v)当∂=5时,方程可变为 p4(p-1)φ(n1)=s(p45),则
若 p=2,那么 s(245)=48=24φ(n1),该方程无解 .
若 p ≥3,由引理 5 可知 :s(p9∂)≤9p∂,注意到 φ(n)=p∂-1(p-1)φ(n1)和 p∂-1(p-1)>9p∂,因此 ,该方程无解.
(vi)当∂=6 时,方程可变为 p5(p-1)φ(n1)=s(p54),则
若 p=2,那么 s(254)=58=25φ(n1),该方程无解 .
若 p ≥3,由引理 5 可知 :s(p9∂)≤9p∂,注意到 φ(n)=p∂-1(p-1)φ(n1)和 p∂-1(p-1)>9p∂,因此 ,该方程无解.
(vii)当∂=7时 ,方程可变为 p6(p-1)φ(n1)=s(p63),则
若 p=2,那么 s(263)=64=26φ(n1),该方程无解 .
若 p ≥3,由引理 5 可知 :s(p9∂)≤9p∂,注意到 φ(n)=p∂-1(p-1)φ(n1)和 p∂-1(p-1)>9p∂,因此 ,该方程无解.
(viii)当∂=8时,方程可变为 p7(p-1)φ(n1)=s(p72),则
若 p=2,那么 s(272)=76=27φ(n1),该方程无解 .
若 p ≥3,由引理 5 可知 :s(p9∂)≤9p∂,注意到 φ(n)=p∂-1(p-1)φ(n1)和 p∂-1(p-1)>9p∂,因此 ,该方程无解.
(ix)当∂=9时,
若 p=2,那么 s(254)=58=25φ(n1),该方程无解 .
若 p ≥3,由引理 5 可知 :s(p9∂)≤9p∂,注意到 φ(n)=p∂-1(p-1)φ(n1)和 p∂-1(p-1)>9p∂,因此 ,该方程无解.
联合(i)到(ix),可得方程有一个解:n=1.
证毕
纠错[4]:曹楠,高丽在西南民族大学学报2009年35卷第5期上发表文章关于数论函数方程φ(n)=S(n7).
在此论文中,证明了 φ(n)=S(n7)有 n=1,64,72,80这4个解。而当 n=64时,φ(64)=32,S(647)=48所以 φ(64)≠S(647)即64不是方程 φ(n)=S(n7)的解。
当 n=72时,φ(72)=24,S(727)=32所以 φ(72)≠S(727)即72不是方程 φ(n)=S(n7)的解。
综上所述,φ(n)=S(n7)的解:n=1,80.
[1] Yi Y.An equation involving the Euler function and Smarandache function[J].Scientia Magna,2005,1(2):73-175.
[2] 黄寿生,陈锡庚.关于数论函数方程 φ(n)=s(n5)[J].华南师范大学学报,2007,(4):41-43.
[3] 郑涛.关于数论函数方程φ(n)=s(n6)[J].中国科教创新导刊,2009,(2):154-154.
[4] 曹楠,高丽.关于数论函数方程φ(n)=s(n7)[J].西南民族大学学报,2009,35(5):992-994.
[5] Ma J P.An equation involving the Smarandache function[J].Scientia Magna,2005,1(2):89-90.
[6] 刘燕妮.一个包含Smarandache函数的方程[J].西北大学学报,2007,37(2):197-198.
[7] 马金萍,刘宝利.一个包含Smarandache函数的方程[J].数学学报,2007,50(5):1185-1190.
[8] 廖思泉,关于数论函数方程φ(n)=S(nt)[J].福州大学学报(自然科学版),2009,37(2):302-304.
[9] 徐哲峰.关于Smarandache函数的值分布[J].数学学报,2006,49(5):1009-1012.
[10] Sndor J.On certain limits for arithmetical functions[J].OctogonMathMag,2007,15(1):280-283.
[11] Erdös P.Problem 6674[J].Amer.Math.Monthly,1991,98:965.
[12] Tabirca S.About S-multiplicative functions[J].Octogon,1999,7:169-170.
[13] Wang Y X.On the Smarandache function,Research on Smarandache Problems in Number Theory Collected papers[M].America Hexis,2004:103-106.
[14] 华罗庚.数论导引[M].北京:科学出版社,1979:28-32.
[15] Farris M,Mitchell P.Bounding the Smarandache function[J].Smarandache Notions J,2002,13(1):37-42.

