混合序列线性形式的强稳定性

陈芬

（中南财经政法大学武汉学院信息系，湖北武汉430079）

0 引言

设｛Xn，n≥1｝是概率空间（Ω，A，P）上的随机变量序列，N是自然数集，Fs＝σ（Xi，i∈S⊂N）为σ－代数.在F中给定σ－代数g，R，令

其中

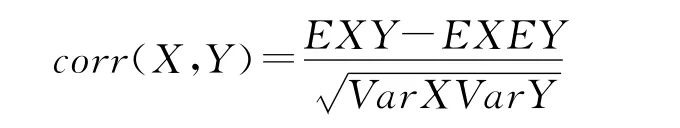
为相关系数，Bradley［1］引入如下的相依系数：对k≥0，令

称随机变量序列｛Xn，n≥1｝是强稳定的，若存在两个常数列｛an，n≥1｝和｛bn，n≥1｝，an↑∞（n→∞），有

称随机变量序列｛Xn，n≥1｝是尾概率一致有界的，若存在非负的随机变量X及正常数C，使对任意的x及n≥1，都有

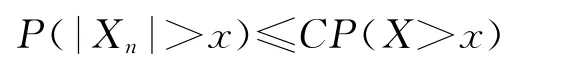
成立，此时记为｛Xn｝＜X.

1 主要结论及证明

引理1 设｛Xn，n≥1｝是混合序列，｛an，n≥1｝是正实数列且an↑∞（n→∞）.若

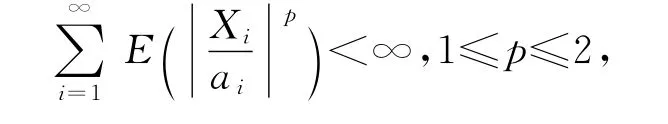
引理1的证明 由文献［6］中的定理4即得.

引理2 设X为随机变量，且对任意的x＞0，都有P（｜X｜＞x）≤CP（V＞x），其中V为非负随机变量，C＞0为常数，则对任意的x＞0，q＞0有

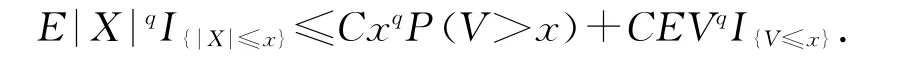
引理2的证明 由积分等式

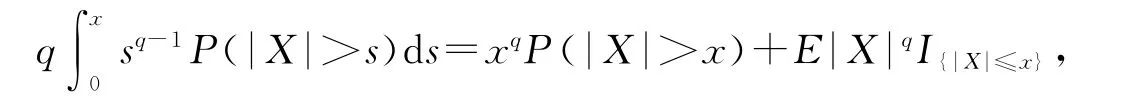
引理3 设｛an，n≥1｝和｛bn，n≥1｝是任意的两个正实数列，cn＝bn／an，bn↑∞，｛Xn，n≥1｝为零均值的随机变量序列且｛Xn｝＜X，对任意的x＞0，定义N（x）＝Card｛n∶cn≤x｝，若其满足：

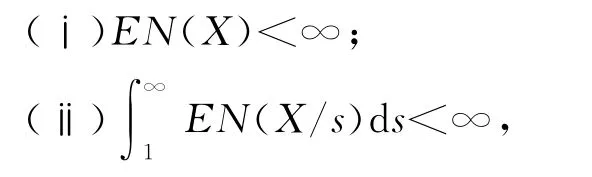
记Yn＝XnI｛｜Xn｜≤cn｝，则

引理3的证明 因为

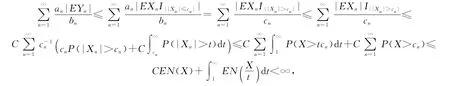
由Kronecker引理知结论成立.

定理1 设｛an，n≥1｝和｛bn，n≥1｝是任意的两个正实数列，cn＝bn／an，bn↑∞，｛Xn，n≥1｝为混合序列且｛Xn｝＜X，对任意的x＞0，定义N（x）＝Card｛n∶cn≤x｝，若下列条件成立：

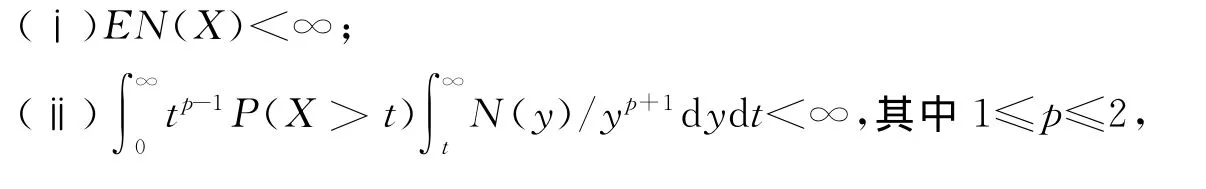
则存在数列｛dn，n≥1｝，使得成立.

定理1的证明 对任意的n≥1，记Yn＝XnI｛｜Xn｜≤cn｝.由于

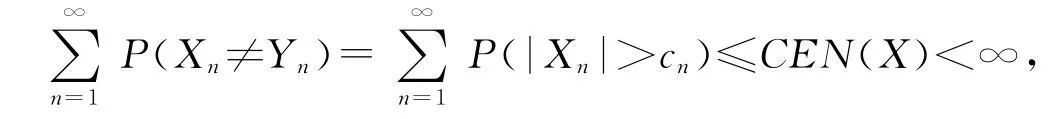
由Borel－Cantelli引理，对数列｛dn，n≥1｝，为证，只须证a.s.即可.如果能证明则取

由引理2有

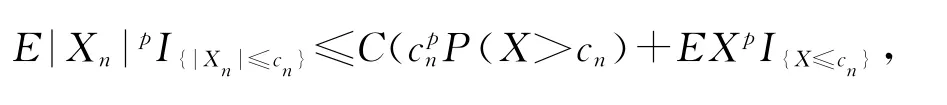
因此有

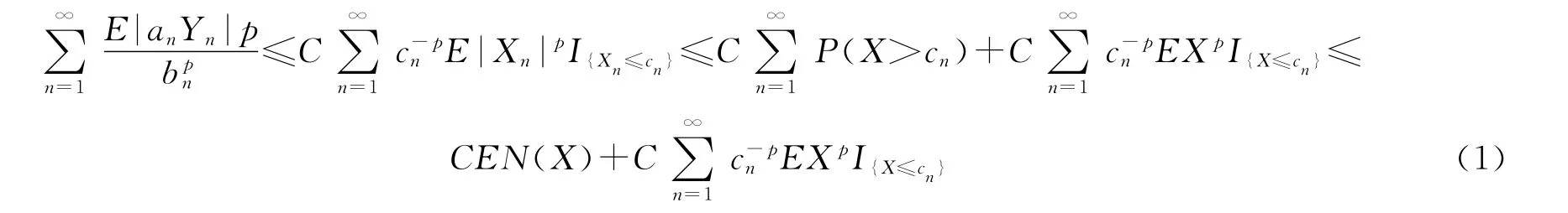
以及

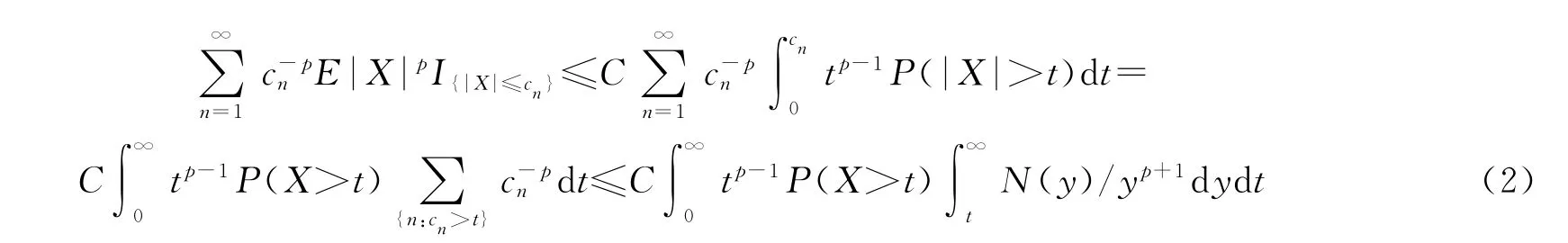
上面最后一个不等式成立基于下列事实：

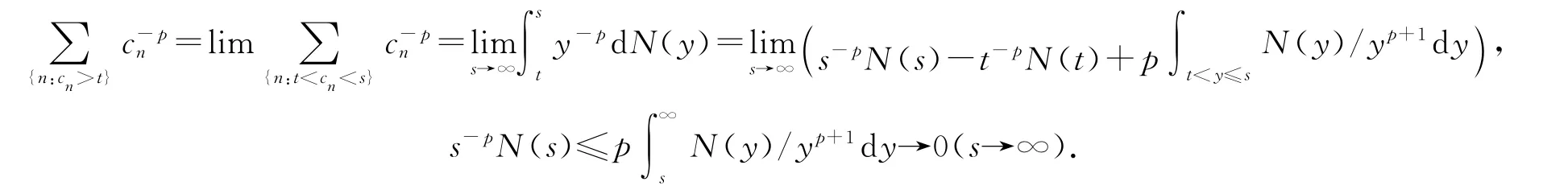
由（1）～（2）式及条件（ⅰ）（ⅱ）有

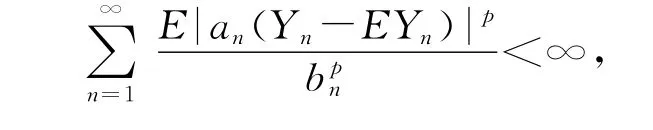
推论1的证明 由定理1及引理3即得.

定理2 设｛an，n≥1｝和｛bn，n≥1｝是任意的两个正实数列，cn＝bn／an，bn↑∞，｛Xn，n≥1｝为～ρ混合序列且｛Xn｝＜X，对任意的x＞0，定义N（x）＝Card｛n：cn≤x｝，若下列条件成立：

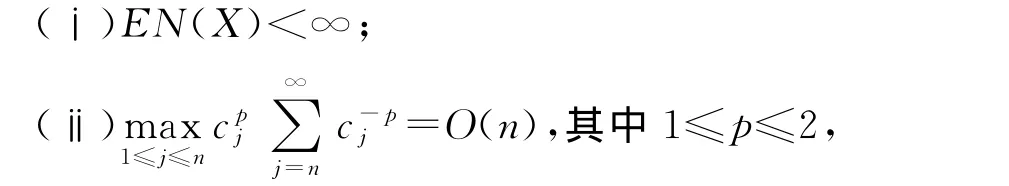
则存在数列｛dn，n≥1｝，使得成立.

定理2的证明 对任意的n≥1，Yn的记号同定理1.由

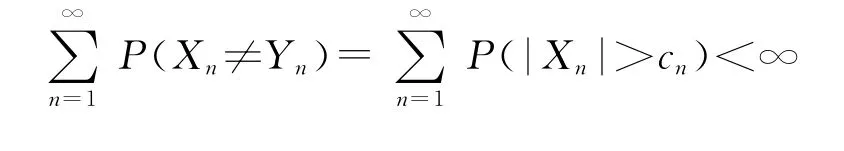
及Borel－Cantelli引理，为证定理2的结论，只须证明

由引理2有

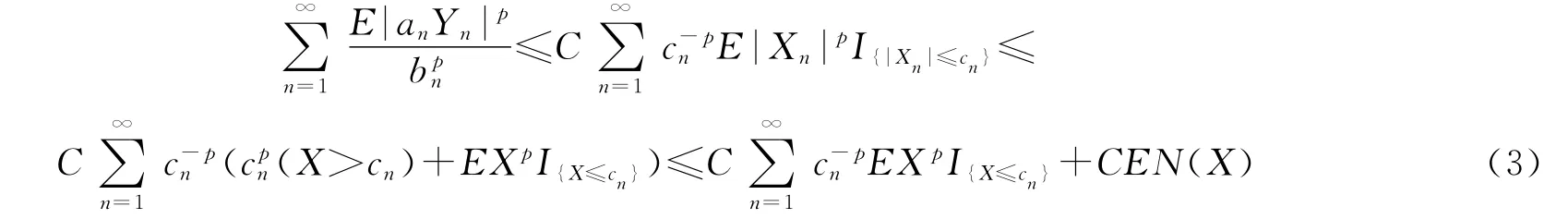
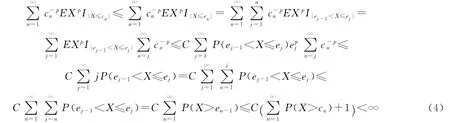
由（3）～（4）式知

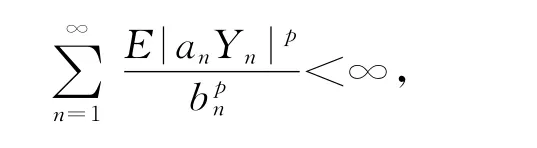
定理3 设｛an，n≥1｝和｛bn，n≥1｝是任意的两个正实数列，cn＝bn／an，bn↑∞，｛Xn，n≥1｝为～ρ混合序列且｛Xn｝＜X，对任意的x＞0，定义N（x）＝Card｛n：cn≤x｝，若下列条件成立：

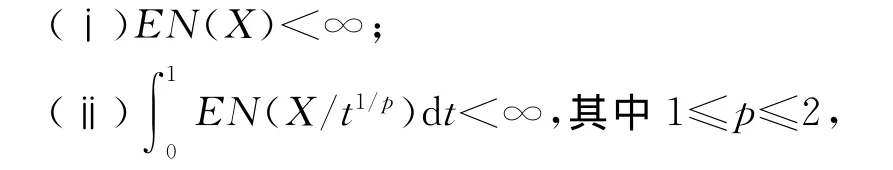
则存在数列｛dn，n≥1｝，使得成立.

定理3的证明 对任意的n≥1，Yn的记号同定理1.只须证明

由于

推论3 设｛Xn，n≥1｝为零均值的～ρ混合序列且满足定理3的条件，如果，则成立.

定理4 设｛an，n≥1｝和｛bn，n≥1｝是任意的两个正实数列，cn＝bn／an，bn↑∞，｛Xn，n≥1｝为零均值的混合序列且｛Xn｝＜X，对任意的x＞0，定义N（x）＝Card｛n：cn≤x｝，若下列条件成立：

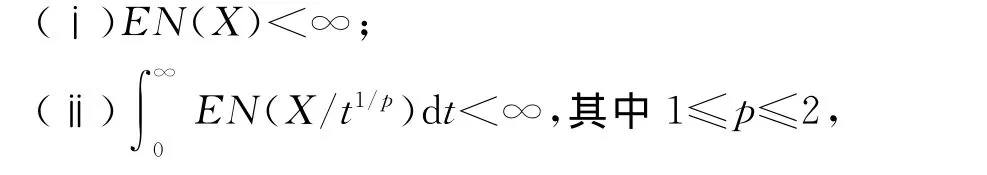
定理4的证明 对任意的n≥1，记Yn＝XnI｛｜Xn｜≤cn｝，Tn＝Xn－Yn.注意到由定理3知为证定理4的结论，只须证明a.s.即可.由于

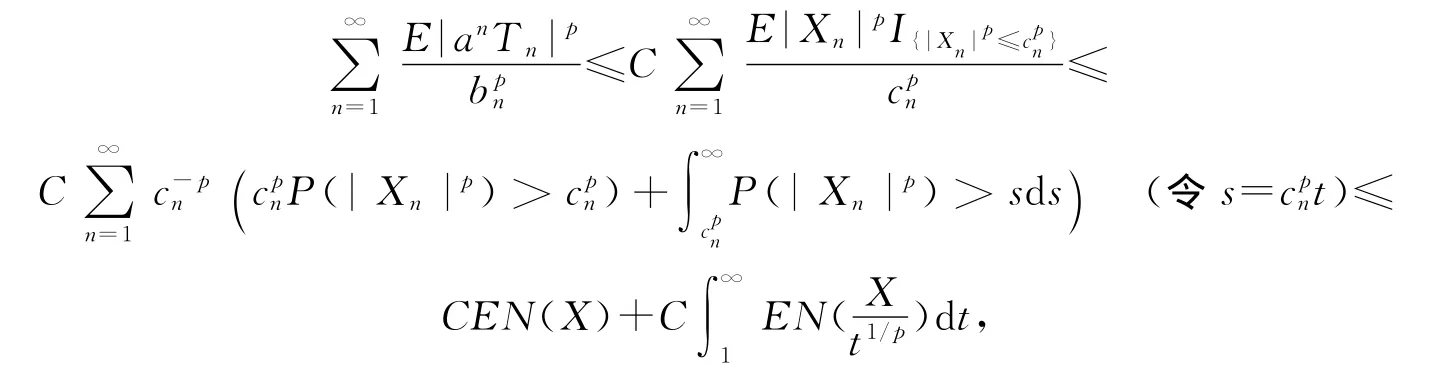
由条件（ⅰ），（ⅱ）有

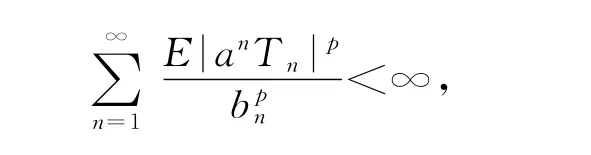
推论4 设｛bn，n≥1｝是任意的正实数列，bn↑∞，｛Xn，n≥1｝为零均值的～ρ混合序列且｛Xn｝＜X，对任意的x＞0，定义N（x）＝Card｛n：bn≤x｝，若下列条件成立：

在推论4中若令bn＝n1／r，n≥1，r＞0，我们可以得到混合序列的Marcinkiewcz型强大数定律成立.

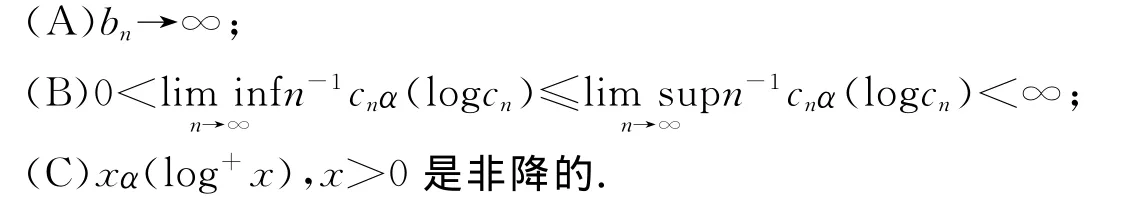
定理5 设｛Xn，n≥1｝是同分布的～ρ混合序列.如果E｜X1｜α（log＋｜X1｜）＜∞，则存在数列｛dn，n≥1｝，使得成立.

定理5的证明 对任意的n≥1，Yn的记号同定理1.因为0＜α（x）↓，bn↑∞.由条件（B），可选取m0≥1，α＞0，β＞0使得当n≥m0时

于是有

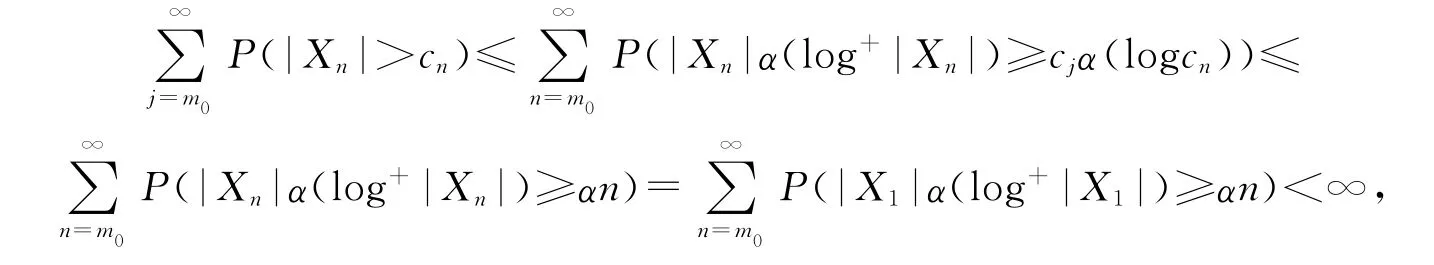
从而有

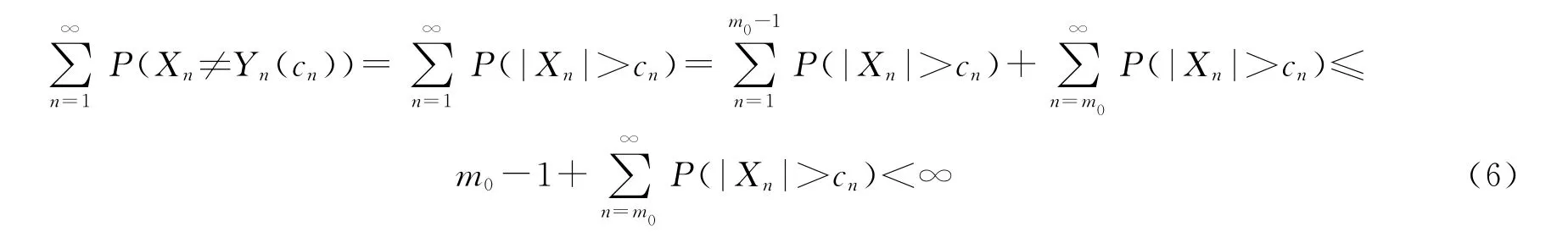
对n≥m≥m0，由（5）式有cn≥αn（α（logcn））－1，从而

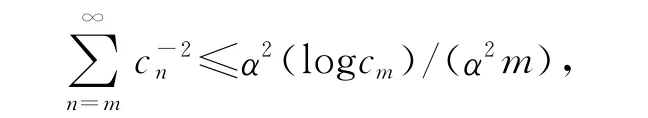
这里m≥m0.于是当m≥m0时有

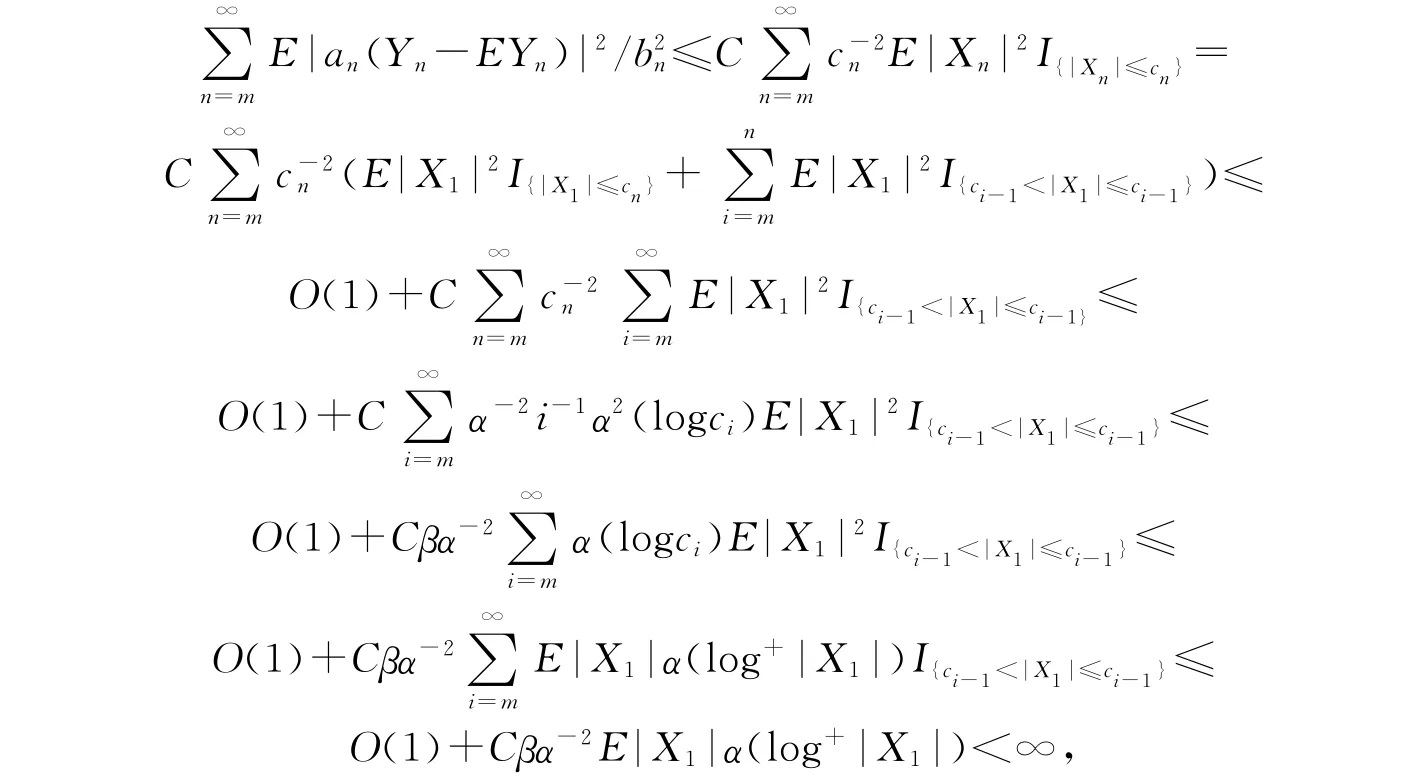
如果｛Xn，n≥1｝不同分布的，我们有下面的结论.

定理6 设｛Xn，n≥1｝是不同分布的～ρ混合序列，如果，其中1≤p≤2，则存在数列｛dn，n≥1｝，使得成立.

定理6的证明 沿用定理1证明中的记号，并采用定理5同样的证明方法，易得

由Borel－Cantelli引理，只要证即可.由于

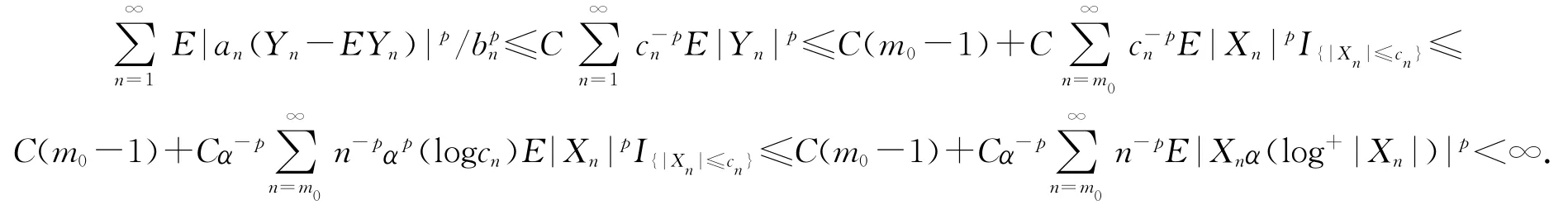
［1］Bradley R C.Eqnivalent mixing conditions for random fields［J］.Annals of Probability，1993，21（4）：1921－1926.

［2］Bradley R C.On the spectral density and asymptotic normality of weakly dependent random field［J］.Theoret Probab，1992（5）：355－374.

［3］Bryc W，Smolenski W.Moment conditions for almost sure convergence of weakly correlated random variables［J］.Proceeding of American Math Society，1993，119（2）：629－635.

［4］杨善朝.一类随机变量部分和的矩不等式及其应用［J］.科学通报，1998，43（17）：1823－1827.

［5］吴群英.～ρ混合序列的若干收敛性质［J］.工程数学学报，2001，18（3）：58－64.

［6］邱德华，甘师信.～ρ混合序列的Hàjek－Rènyi型不等式及强大数律［J］.数学的实践与认识，2007，37（2）：107－111.

［7］吴群英.混合序列的概率极限理论［M］.北京：科学出版社，2006.

［8］甘师信.B值随机元阵列加权和的收敛性及大数定律［J］.武汉大学学报：理学版，2000，43（5）：569－574.

［9］甘师信，张峰，叶臣.B值鞅差序列加权和的收敛性及大数定律［J］.武汉大学学报：理学版，2000，46（3）：266－268.

［10］Chandra T K.Uniform integrability in the Cesáro sence and the weak law of large numbers［J］.sankhyā：The India Journal of Statistics，1989（A）：309－317.

［11］Utev S，Peligrad M.Maximal inequalities and an invariance principale for a class of weakly dependent random variables［J］.Theoret Probab，2003，16（1）：101－115.