基于Dijkstra算法的机器人避障最短线路模型

孙忠民

(潍坊工程职业学院，山东 青州 262500)

1 问题重述

研究机器人避障问题:一个800×800的平面场景图，在原点O(0，0)点处有一个机器人，它只能在该平面场景范围内活动。图中有12个不同形状的区域是机器人不能与之发生碰撞的障碍物，见图1。

图1 800×800平面场景图

目标点分别为A(300，300)，B(100，700)，C(700，640)。机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径。机器人不能折线转弯，转弯路径由与直线路径相切的一段圆弧组成，也可以由两个或多个相切的圆弧路径组成，但每个圆弧的半径最小为10个单位并要求目标点与障碍物的距离至少超过10个单位。为了不与障碍物发生碰撞，同时要求机器人行走线路与障碍物间的最近距离为10个单位，否则将发生碰撞，若碰撞发生，则机器人无法完成行走。

已知机器人直线行走的最大速度为v0=5个单位/秒。机器人转弯时，最大转弯速度为v=v(ρ)=，其中ρ是转弯半径。如果超过该速度，机器人将侧翻，行走失败。

建立机器人从区域中一点到达另一点的避障最短路径和最短时间路径的数学模型。

2 问题分析

2.1 问题1

由于机器人从O绕过障碍物到达目标点的路径有多条，首先，在忽略路径中拐角处圆弧长度情况下，利用有向图路径寻优问题的Dijkstra算法找出多条路径中的最短线路;其次，对于最短线路中只经过一个拐角的情况(O→A)，机器人要安全经过需在拐角处放置一个半径是10单位的安全防碰圆，利用简单线圆结构精确求出O到A的最短路径;然后，对最短线路中有多个拐角(O→B、O→C)进行分析，两个相邻拐角的转弯方式有两种，一是路径与两圆心连线相交，二是路径与两圆心平行，这时需要做简单地变换求出最短路径;最后，对O→A→B→C→O中经过拐点A、B、C的情况进行分析，把A、B、C分别看作圆弧上的点，利用线圆结构，求出经过拐点处的最短路径。

表1 障碍物的数学描述表

2.2 问题2

利用问题1求出的O→A的最短距离路径，由于转弯速度与圆弧半径有关，转弯半径越大转弯处的速度越快，在半径10的基础上适当扩大拐点处的转弯半径，可使从O到A的行走时间最短。由于机器人到障碍物的最短距离为10，可知机器人行走路径经过定点(72.9289，217.0711)，首先考虑圆心在(80，210)情况得出从O到A的时间;然后考虑圆心位置、半径大小变化的情况，建立以圆心坐标为变量的二元函数，通过求二元函数在(80，210)附近的极值得出所需时间，并对两种情形进行比较，最终求得最短时间路径。

3 模型假设

3.1 假设机器人的体积为0，即为一个点

3.2 假设其速度是瞬间变化的，即加速或减速时间为0

3.3 假设机器人行走线路与障碍物间的最近距离至少为10个单位

3.4 假设机器人行走时未超过直线行走最大速度和最大转弯速度

3.5 假设Dijkstra算法中有向图中的权重为两点间的距离

3.6 假设每个障碍物从左下角开始按顺时针分别标为①②③④

4 符号说明

L:路径的总长度;di:第i段切线的长度;lj:第j段圆弧的长度;ρ:转弯半径;k:障碍物上的任意点与行走路径之间的最短距离;Oi:第i段切线的圆心坐标(xoi，yoi)

5 模型建立

5.1 从O到目标点的最短路径选择

机器人从O到各目标点的路径有很多，利用图论中求最短路问题的Dijkstra算法，对从O到各点的路径进行选择，分别找出O→A，O→B，O→C，O→A→B→C→O的最短路径。

5.1.1 Dijkstra最短路径算法

如果指定了起始节点，则该点到其他所有节点的最短路径可以一次性求出。假设结点个数为n，起始节点为s，则该算法步骤为:

(1)初始化:建立三个向量存储各节点的状态，其中visiteb表示各节点是否更新，初始值为0;dist存储起始点到本节点最短距离，初始值为无穷;parent向量存储到本节点上一个节点，默认值为0。另外设起始节点处dist(s)=0。

(2)循环求解:让I做n-1次循环，更新能由本节点经过一边到达的节点信息，并更新有本节点可以到达的未访问节点的最短路径信息。循环直到所有未访问节点完全处理完成。

(3)提取到终止接点t的最短路径，利用perent向量逐步提取最优路径。

5.1.2 从O到A的路径选择

表2 O到A的有向图节点数据及最短路径

5.1.3 从O到B的路径选择

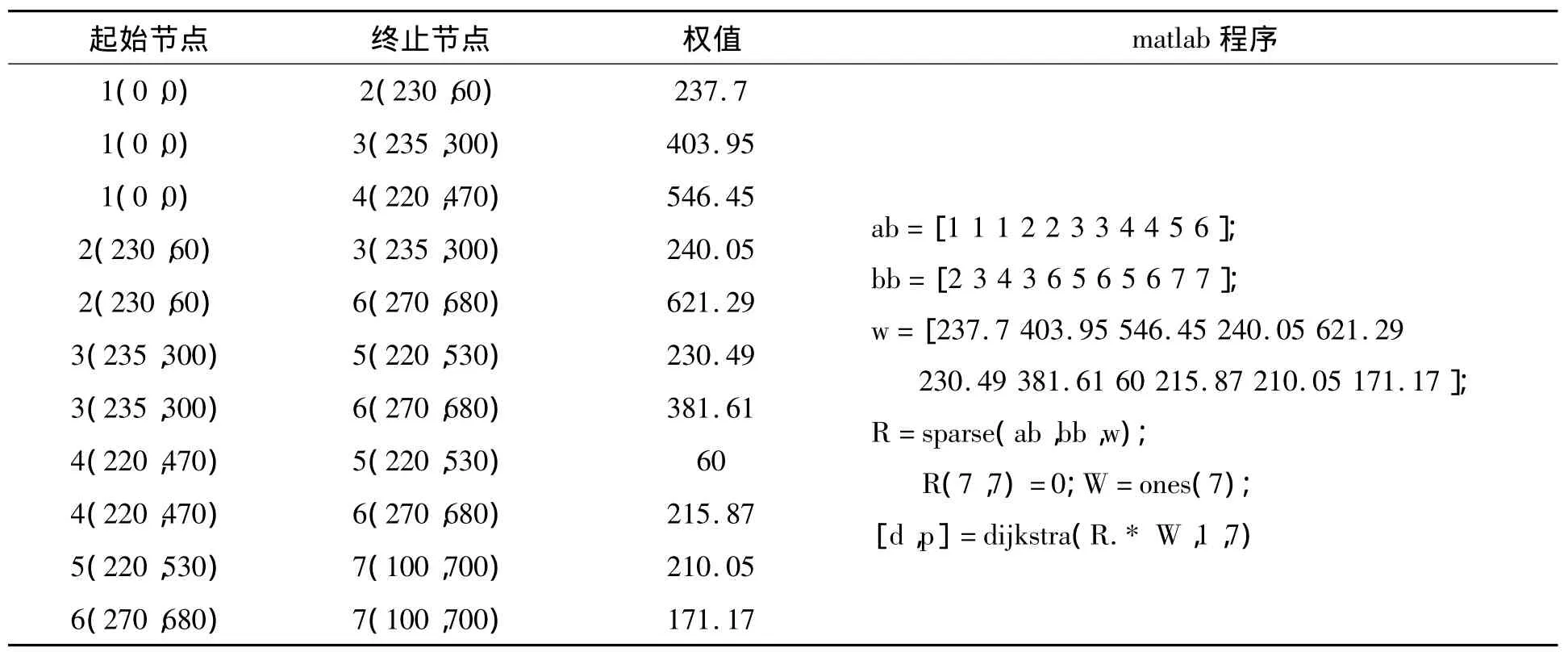
表3 O到B的有向图节点数据及matlab程序

O到B 的最短路径为:(0，0)→(60，300)→(150，435)→(220，470)→(220，530)→(150，600)→(100，700)，最短路径长度:d=816.5。

5.2 问题1的模型建立

5.2.1 模型1

由O到A的最短路径是绕障碍物5的左上角G(80，210)到达目标点A，见图2。

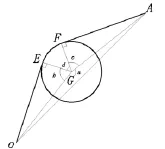
图2 O通过G到达A的最短路径

图3 O到B行径的圆弧求解图

E和F分别为机器人经过圆G拐点分别于隔离危险线拐角小圆弧的切点，设O(x1，y1)为起点，A(x2，y2)为目标点，E(x3，y3)和 F(x4，y4)，圆心为 G(x5，y5)，圆的半径为 R=10，∠AGO=a，∠OGE=b，∠EGF=c，∠AGF=d，从O到A的长度为L。由图2可得:

5.2.2 模型2

由O到B的最短路径为:(0，0)→(60，300)→(150，435)→(220，470)→(220，530)→(150，600)→(100，700)到目标点B，可以看出不能用简单的线圆结构求出最短路径，需要做简单的变换求弧长，见图3。

由两圆弧的切线IJ向下平移到圆心H交KJ的延长线于P，两圆的半径均为R，要求LJ的弧长，需要求出c的弧度。由图3很容易看出

同理，机器人从O到目标点C的最短路径，由模型1、模型2可求。

5.2.3 模型3

机器人从O点出发，由O→A→B→C→O的最短路径，机器人在行径路程中经过不同的拐点A、B、C，由于机器人行走的拐点半径不小于10个单位，所以需要对拐点处机器人的绕线路径进行分析。

以A点为例进行分析，过A点作圆弧并过D、O两点做该圆的切线，切点为E、F。可知要使O经过A到D的路径最短，其圆弧的圆心O＇必在∠OAD的角平分线上，见图4。

图4 拐点路径求解图

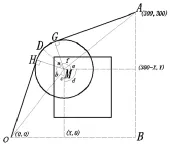
图5 O到A的最短时间路径图

设圆的半径为 ρ ，圆心 O ＇(x，y)，O(x1，y1)，A(x0，y0)，D(x2，y2)，由图 4 可知:

综上所述，拐点A处的最短路径可求，同理可得过B、C两点的最短路径。

5.3 问题2的模型建立

结合问题1求出的O→A的最短路径，由于转弯速度与圆弧半径有关，转弯半径越大转弯处的速度越快，在半径10的基础上适当扩大拐角处的转弯半径，可使从O到A的行走时间最短。由于机器人到障碍物的最短距离为10，可知机器人行走路径经过定点首先考虑圆心在(80，210)，半径为10的情况得出从O到A的时间，然后考虑圆心、半径变动的情况，建立最短时间路径的的二元函数，其中圆心坐标为变量，通过求二元函数在(80，210)附近的极值得出所需时间，并对两种情形进行比较，最终求得最短时间路径。

5.3.1 模型4

机器人与障碍物间的最近距离为10，已知O(0，0)、A(300，300)，以障碍物左上顶点为圆心，半径为10画圆与正方形的对角线交障碍物外一点，在障碍物中任选一点M(x，y)，以MD为半径ρ作圆，分别过O、A做圆的切线交于点H、G连接MH、MG、MO、MA。借助模型3的结论可得:

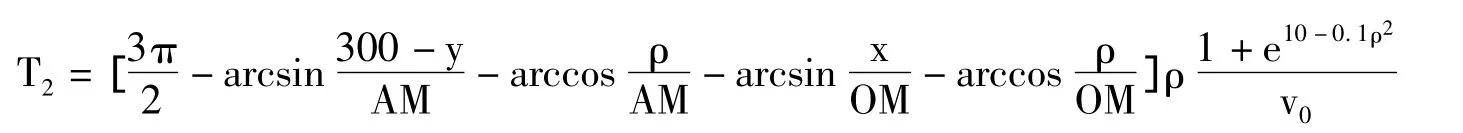
综上所述总时间:T=T1+T2

求T的最小值即为最短时间，所经过的路径即为最短时间路径。

6 模型求解

机器人从点O到目标点M0，路径是由圆弧和线段组成，设有m条线段，n条圆弧。

6.1 问题1求解

(1)利用模型1得到O到A的最短路径长度为471.04，所用时间为99.13。

(2)利用模型1、2得到O到B的最短路径长度为853.71，所用时间为179.07。

(3)利用模型1、2得到O到C最短路径长度为:1087.97，所用时间为217.59。

(4)利用模型1、2、3得到O经过A、B、C回到O的最短路径长度为2701.54，所用时间为568.57。

6.2 问题2求解

利用模型4，以圆心坐标为变量建立最短时间T的二元函数，利用求二元函数在(80，210)附近的极值的方法，得出所需时间T，并与圆心固定在(80，210)情形进行比较，最终求得从O到A最短时间路径。O到A的最短时间路径为:从O点到切点H(70.2475，212.6321)，经圆弧到切点(77.1135，220.0683)经线段到A(300，300)。拐角处圆心M的坐标为(81.1678，209.0244)，半径r为11.5，最短时间路径l长为471.68，最短时间为94.8971。

7 模型的评价与改进

7.1 优点

(1)运用Dijkstra搜索算法对路径进行筛选，有普遍性并便于推广。

(2)模型简单易懂，便于实际检验及应用。

(3)模型优化后用解析几何进行求解，精确度较高。

7.2 缺点

(1)此模型适于全局规划，获得精确解却失去了效率。

(2)在障碍物较多且形状不规则时，模型需要进一步改进。

7.3 模型改进

模型也可采用蚁群优化算法，利用差分演化算法进行信息素的更新，同时对可能出现的停滞现象，在信息素更新时加入混沌扰动因子，采用一个新的评价函数增强算法的逃逸能力，避免了路径死锁现象，高效率地搜索出最优路径，即使在障碍物非常复杂的环境下，也能快速地规划出安全的最优路径，是一种与本模型相符的有效改进方法。

［1］赵静，但琦.数学建模与数学实验［M］.北京:高等教育出版社，2000.

［2］姜启源.数学模型［M］.北京:高等教育出版社，2003.

［3］邦迪.图论及其应用［M］.西安:西安科学出版社，1984.

［4］薛定宇，陈阳泉.高等应用数学问题的MATLAB求解［M］.北京:清华大学出版社，2004.